|
Was ist das Zweiersystem?
Das Zweiersystem ist eine Stellenschreibweise der Zahlen, bei der nur
die beiden Ziffern 0 und 1 verwendet werden.
Das sind die ersten 15 Zahlen:
| 0
0
- |
1
1
I |
10
2
II |
11
3
III |
100
4
IV |
101
5
V |
110
6
VI |
0111
7
VII |
1000
8
VIII |
1001
9
IX |
1010
10
X |
1011
11
XI |
1100
12
XII |
1101
13
XIII |
1110
14
XIV |
1111
15
XV |
Darunter stehen dieselben Zahlen, geschrieben im Zehnersystem und mit römischen
Ziffern.
Die Darstellung im Zweiersystem ist zwar umständlich, schon weil
die Anzahl der Stellen schnell wächst, aber im Zeitalter der Informationstechnik
hat sie eine große Bedeutung erlangt.
1 und 0 können gedeutet werden als an-aus, wahr-falsch, ja-nein,
geschlossen-offen.
Das Zweiersystem heißt auch Dualsystem, Binärsystem
oder binäres System.
Ich füge noch für den Gebrauch von Suchmaschinen die englischen
Bezeichnungen binary numeral system,
kürzer binary system
oder ganz kurz binary hinzu.
Erklärung des Zweiersystems
top
Die Zweiersystems ist im Prinzip wie das Zehner- oder Dezimalsystem
aufgebaut.
Das Zehnersystem ist eine Stellenwertsystem. In einer Zahl wie 10110
haben die drei Einsen unterschiedliche Bedeutung. Es kommt darauf an, wo
sie stehen. Diese unterschiedlichen Bewertungen zeigt die Tabelle.
...
... |
10000er
1 |
1000er
0 |
100er
1 |
10er
1 |
Einer
0 |
Die "Stufenzahlen" 10, 100, 1000, ... der Tabelle sind Potenzen von 10.
Im Zweiersystem nimmt die Tabelle folgende
Form an.
| ... |
256er |
128er |
64er |
32er |
16er |
8er |
4er |
2er |
Einer |
Hier heißen also die Stufenzahlen 2,4,8,16,... und sind Potenzen
von 2.
Es sei die Zahl 10110 im Zweiersystem gegeben.
Sie wird in die Tabelle eingetragen:
...
... |
256er
0 |
128er
0 |
64er
0 |
32er
0 |
16er
1 |
8er
0 |
4er
1 |
2er
1 |
Einer
0 |
Man liest ab: 10110=2+4+16=22. Nur wenn in der Tabelle eine 1 steht, wird
die Stufenzahl berücksichtigt.
Diese Schreibweise ist missverständlich. Man schreibt besser (10110)2,
damit keine Verwechslung mit der Zehnerdarstellung (10110)10
auftritt. Man hat vereinbart, dass nicht gekennzeichnete Zahlen dem Zehnersystem
angehören.
Es ist günstig, für (10110)2
eine einfachere Schreibweise zu verwenden. Man schreibt in vielen Schulbüchern
die 1 als Strich und erhält dann
 .
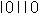Diese Darstellung kann ich auf dieser Seite nur in .gif-Bildern verwenden,
da der einfache Strich im normalen Zeichensatz nicht vorkommt. Die Ersatzzeichen
|, I oder l sind nicht zu gebrauchen.
Die Zahl (10110)2 wird gelesen als "Eins, Null, Eins, Eins,
Null" oder "Strich, Null, Strich, Strich, Null".
Umrechnungen top
Vom Zweiersystem zum Zehnersystem
Es stellt sich die Aufgabe, eine Zahl wie (100111)2 ins
Zehnersystem zu übertragen, schon damit man eine Vorstellung von der
Größe hat. Der Weg wurde oben schon dargestellt.
...
... |
256er
0 |
128er
0 |
64er
0 |
32er
1 |
16er
0 |
8er
0 |
4er
1 |
2er
1 |
Einer
1 |
Man trägt die Zahl in die Tabelle ein und liest (100111)2
=1+2 +4+32=39 ab. Man beginnt bei der Summenbildung auf der rechten Seite.
Das ist praktischer.
Hier sind noch drei Beispiele:
(111000)2 =8+16+32=56, (110011)2 =1+2+16+32=51,
(11111111)2 =1+2+4+8+16+32+64+128=255.
Vom Zehnersystem
zum Zweiersystem
Das umgekehrte Problem, zu einer Zahl wie 38 die Schreibweise im Zweiersystem
zu finden, erfordert eine Vorbereitung:
Man muss 38 in eine Summe von Zweierpotenzen zerlegen. Dabei beginnt
man mit der größten Potenz, die kleiner ist als die gegeben
Zahl, und zerlegt dann weiter.
38=32+6=32+4+2. Das führt in der Tabelle zu folgendem Eintrag
...
... |
256er
0 |
128er
0 |
64er
0 |
32er
1 |
16er
0 |
8er
0 |
4er
1 |
2er
1 |
Einer
0 |
Die Zahl 38 hat also die Darstellung 38=(100110)2 .
Hier werden die drei Beispiele von oben entsprechend umgeformt.
56=32+16+8=(111000)2 , 51=32+16+2+1=(110011)2,
255=128+64+32+16+8+4+2+1=(11111111)2 .
Halbierungsverfahren
Es gibt einen anderen Weg, eine Zahl vom Zehnersystem ins Zweiersystem
zu übertragen.
Das wird am Beispiel der Zahl 116 erklärt:
116...58...0
058...29...0
029...14...1
014...07...0
007...03...1
003...01...1
001...00...1 |
..... |
Stelle drei Spalten bereit.
Schreibe oben links in die erste Spalte die gegebene Zahl 116.
Dividiere sie durch 2 und schreibe die halbe Zahl 58 in die zweite
Spalte und in die dritte Spalte den Rest 0.
Schreibe die mittlere Zahl 58 in die nächste Zeile und wiederhole
das Halbieren.
Führe das Halbieren fort, bis in der mittleren Spalte Null steht.
Notiere die Reste von unten nach oben. Das ist in diesem Falle 1110100.
Das ist die Darstellung im Zweiersystem. |
Erklärung:
Die Zeilen kann man schreiben als 116=58*2, 58=29*2, 29=14*2+1, 14=7*2,
7=3*2+1, 3=1*2+1.
Man ersetzt die halben Zahlen nacheinander: 116=58*2=(29*2)*2=
... =(((((1*2+1)*2+1)*2)*2+1)*2)*2
Im Term steckt die dritte Spalte: ((((((0*2+1)*2+1)*2+1)*2+0)*2+1)*2+0)*2+0
Multipliziert man diesen Term aus, so erhält man 116=26
+25 +24 +22.
Fünfersystem top
Das Zweiersystem benötigt zur Darstellung einer Zahl nur zwei
Ziffern und ist wegen dieser Einfachheit gewohnheitsbedürftig. Deshalb
ist es vielleicht hilfreich, wenn man ein weiteres Zahlensystem vorstellt
mit mehr Ziffern. Das soll das Fünfersystem sein, bei dem man mit
0, 1, 2, 3 und 4 auskommt.
Das Fünfersystem hat die Stufenzahlen 5, 5²=25, 5³=125,...,
die zu folgender Tabelle führen.
3125
1 |
625
4 |
125
4 |
25
1 |
5
2 |
1
3 |
Die Zahl 144123 ist eingetragen. Man liest ab: (144123)5=1*3125+4*625+4*125+1*25+2*5+3=6163.
Wie im Fünfersystem gezählt wird,
steht in der zweiten Zeile der folgenden Tabelle.
0
0
0
- |
1
1
1
I |
10
2
2
II |
11
3
3
III |
100
4
4
IV |
101
10
5
V |
110
11
6
VI |
0111
12
7
VII |
1000
13
8
VIII |
1001
14
9
IX |
1010
20
10
X |
1011
21
11
XI |
1100
22
12
XII |
1101
23
13
XIII |
1110
24
14
XIV |
1111
30
15
XV |
Verknüpfungen top
Unter Verknüpfungen versteht man die Grundrechenarten Addition,
Subtraktion, Multiplikation und Division.
| 1+1=10 |
Das ist wohl die berühmteste Verknüpfung. Liest sie ein Mensch
mit einem gesundem Menschenverstand, so reagiert er mit Kopfschütteln.
Vielleicht wird er hellhörig. Ein Eingeweihter denkt an 1+1=(10)2, |
Deshalb war "1+1=10" einmal ein raffiniert abgefasster Buchtitel.
Beim schriftlichen Addieren braucht man
im Zehnersystem das kleine Einsundeins, beim Multiplizieren das kleine
Einmaleins. Das sind die Summen und Produkte einstelliger Zahlen, die man
auswendig lernen muss.
Im Zweiersystem sind das nur die vier Summen 0+0=0, 0+1=1, 1+0=1 und
1+1=(10)2 und die Produkte 0*0=0, 0*1=0, 1*0=0 und 1*1=1. Also
muss man sich nur 1+1=(10)2 merken. Im diesem Kapitel heißt
es einfacher 10 anstatt (10)2 .
An Hand der beiden Zahlen (100011)2
und (111)2 werden die schriftlichen Rechenverfahren erklärt.
Addition
... ... |
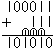Man schreibt die Zahlen untereinander und addiert stellenweise von
rechts nach links. Man beginnt mit 1+1=2=10. Die Ziffer 0 schreibt man
hin und 1 als Übertrag (Wie heißt es so schön? Null hin,
Eins im Sinn.). Dann folgt 1+1+1=3=11. Man schreibt 1 hin und notiert den
Übertrag 1. |
Jetzt sollte klar sein, wie man weiter verfährt.
Subtraktion
... ... |
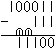Wieder schreibt man die beiden Zahlen untereinander. Die ersten beiden
Einsen führen unten zu 0. Dann muss man 1+x=10 lösen. Es ist
1+1=10. Man schreibt 1 hin und vermerkt den Übertrag 1. Die gleiche
Überlegung erfordern die nächsten beiden Spalten. |
Multiplikation
... ... |
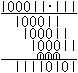Nach dem üblichen Verfahren schreibt man die Faktoren nebeneinander
und beginnt mit der Viererstelle ("Hunderter"): 100011 *1=100011.
Dann folgt die gleiche Zeile noch zweimal, wird aber nach rechts verschoben.
Die spaltenweise Addition schließt sich an. |
Division
... ... |
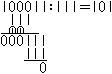Die erste Division ist 1000:111="1". Die zweite Zeile heißt dann
111. Die Differenz ist 1. Holt man die nächste 1 herunter, so ist
11:111 nicht möglich. Also steht oben rechts die Zahl 0. Die nächste
Stelle, die man herunterholt, führt zu 111:111=1. Also ist 101 der
gesuchte Quotient. |
Andere Rechnung
Man kann die beiden gegebenen Zahlen auch ins Zehnersystem übertragen,
rechnen und wieder zurück ins Zweiersystem gehen.
Die Zahlen sind (100011)2 = 1+2+32 = 35 und (111)2
= 1+2+4 = 7.
Damit handelt es sich oben um die Terme
| 35+7=42=32+8+2=(101010)2 |
35-7=28=16+8+4=(11100)2 |
35*7=245=(11110101)2 |
35:7=5=4+1=(101)2 |
Wer das schriftliche Rechnen im Zweiersystem üben will, kann so leicht
weitere Beispiele finden.
Bruchzahlen
Es ist üblich, eine rationale Zahl als Bruch oder als Summe aus
einer ganzen Zahl und Bruch (früher gemischte Zahl genannt) darzustellen.
Beispiele sind 7/20, 12/33 oder 7 5/12.
Um ins Zweiersystem zu gelangen, ersetzt man jede Zahl durch eine Darstellung
im Zweiersystem. Das ist nicht mehr als eine Schreibübung und soll
nicht weiter verfolgt werden.
Interessanter ist die Übertragung der Dezimalbruchdarstellung.
Ein Dezimalbruch hat einen Vorteil: Er ergibt eine gute Vorstellung
von der Größe des Bruches. Der Nachteil ist, dass die Darstellung
wegen der Periode umständlich ist.
Drei Beispiele: 7/20=0,35 12/33=0,713636...
7 5/12=7,41666...
Die Zahlen repräsentieren die drei möglichen Darstellungen
eines Dezimalbruches, die endliche, die rein-periodische und die gemischt-periodische.
Man kann sich überlegen, dass allein der Nenner bestimmt, welche Klasse
vorliegt.
Im ersten Fall ist der Nenner eine Zahl, die nur 2 und 5 als Teiler
hat (20=2*2*5).
Im zweiten Falle hat der Nenner weder 2 noch 5 (33=3*11) als Teiler.
Im dritten Fall hat der Nenner mindestens eine 2 oder 5, aber auch
mindestens einen von 2 und 5 verschiedenen Teiler (12=2*2*3).
Es macht keine Mühe, Zahlen mit Nachkommastellen
im Zweiersystem zu konstruieren.
Eine endliche Darstellung ist (0,011)2 , eine rein-periodische
ist (0,011011011...)2 und
eine gemischt-periodische ist (0,10010101...)2
.
Die Bedeutung der Nachkommastellen entnimmt man der folgenden Tabelle.
Einer ( 20 )
0 |
"2-tel" ( 2-1 )
0 |
4-tel ( 2-2 )
1 |
8-tel ( 2-3 )
1 |
16-stel ( 2-4 )
. |
32-stel ( 2-5 )
. |
Die Zahl (0,011)2 ist eingetragen. Es ist 1/4+1/8=3/8.
Nun benötigt man ein Verfahren, um auch die beiden anderen Zahlen
mit einer Periode ins Zehnersystem zu übertragen, schon damit man
weiß, mit welchen Zahlen man es zu tun hat.
Umwandlungen
Da gibt es das "x-Verfahren". Es wird auf (0,011011011...)2
und (0,10010101...)2 angewandt.
... ... |
... ... |
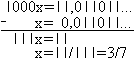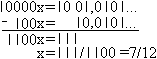Man multipliziert die gegebene Zahl zweimal so, dass rechts des Kommas
gleiche Ziffern untereinander stehen.
Beim Subtrahieren fallen die Nachkommastellen dann weg. |
Die x-Methode ist aus den Lehrbüchern der Schule verschwunden. Die
Methode ist umstritten, weil die Subtraktion von unendlichen Reihen ohne
Kenntnis der Grenzwertsätze problematisch ist. Mein Argument: Es funktioniert.
Ergebnis: Für die drei Zahlen vom Anfang dieses Kapitels gilt
also: (0,011)2=3/8, (0,011...)2
=3/7 und (0,10010101...)2 =7/12.
... ... |
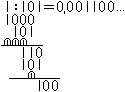Will man zu einem beliebigen Bruch die Darstellung im Zweiersystem
bestimmen, kann man das normale Divisionsverfahren verwenden.
Das wird demonstriert am Beispiel 1/5=(0,0011)2
Die Periode wird auf dieser Seite blau gekennzeichnet.
Normalerweise setzt man einen Strich über die Periode. |
Beispiele
Das sind die ersten Stammbrüche:
| 1/2=(0,1)2 |
1/3=(0,01)2 |
1/4=(0,01)2 |
1/5=(0,0011)2 |
1/6=(0,001)2 |
1/7=(0,001)2 |
| 1/8=(0,001)2 |
1/9=(0,000111)2 |
1/10=(0,0011)2 |
1/11=(0,0001011101)2 |
1/12=(0,0001)2 |
|
Der Bruch 1/7 hat die Darstellung 1/7=(0,001)2
. Die Periodenlänge ist drei und muss es auch für die Brüche
2/7, 3/7, ... sein.
Es gilt tatsächlich:
| 1/7=(0,001)2 |
2/7=(0,010)2 |
3/7=(0,011)2 |
4/7=(0,100)2 |
5/7=(0,101)2 |
6/7=(0,110)2 |
Periode
Schwierig ist das Problem der Periode und der Periodenlänge. Es
folgt ein kleiner Einblick.
Die Periode steht im Zusammenhang mit der Eulerschen Funktion phi(n).
Da wird jeder natürlichen Zahl n (n>1) die Anzahl aller natürlichen
Zahlen <n , die zu n teilerfremd sind, zugeordnet.
Ist zum Beispiel n eine Primzahl p, so ist phi(p)= p-1.
Für die ersten Zahlen gilt:
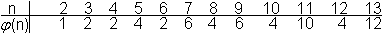Der folgende Satz gilt für alle Ziffernsysteme.
Die Periodenlänge k ist für eine reinperiodische Entwicklung
von a/b ein Teiler von phi(b). Es gilt insbesondere k<=phi(b).
Quelle: (1), Seite 368
Unter dem Gesichtspunkt der Periodenlänge
kann man sich noch einmal die Tabelle der Stammbrüche ansehen.
| 1/2=(0,1)2 |
1/3=(0,01)2 |
1/4=(0,01)2 |
1/5=(0,0011)2 |
1/6=(0,001)2 |
1/7=(0,001)2 |
| 1/8=(0,001)2 |
1/9=(0,000111)2 |
1/10=(0,0011)2 |
1/11=(0,0001011101)2 |
1/12=(0,0001)2 |
|
Die Periode 9 bzw. 1
Eine Merkwürdigkeit der Dezimalbruchdarstellung ist, dass man
die Zahl 1 auch durch 0,9999... darstellen
kann.
Die Erklärung liefert der Grenzwert s der geometrischen Reihe
9/10+9/10²+9/10³+...
Er ist s=a/(1-q)=(9/10)/(1-1/10)=(9/10)/(9/10)=1.
Entsprechend ist (0,1...)2=1. Grund: 1/2+1/2²+1/2³+...
hat den Grenzwert (1/2)/(1-1/2)=1.
Man lässt im Zehnersystem ganz allgemein die Periode 9 nicht zu,
denn eine nichtperiodische Zahl wie 1 soll keine periodische Darstellung
haben. Entsprechend ist im Zweiersystem die Periode 1 nicht zulässig.
Logikus top
Als sich in den 1960er Jahren abzeichnete, dass der Computer in unserem
täglichen Leben eine immer größere Rolle spielen
würde, gab der Kosmos Spielcomputer Logikus (1969) vielen einen
kleinen Einblick, "wie das so mit Null und Eins funktioniert".
Ich besitze ihn noch und habe ihn für diese Seite noch einmal
"programmiert". Dazu wurde ein Geflecht aus blauen Drähten gesteckt.
... ... |
Bewegt man nacheinander die roten Schieber nach oben, so zeigen die
vier mittleren Glühlämpchen die Zahlen 0 bis 9 im binären
System an.
Damit man hier die Glühlämpchen besser sieht, wurde die Abdeckung
abgenommen und mit Gelb und Weiß etwas nachgeholfen. So erkennt man,
dass dem roten Schieber 5 unten die Zahl 0101 oben zugeordnet ist.
Die folgende logische Schaltung wurde beim Logikus umgesetzt.
|
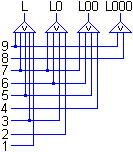
Später konnte die Schaltung mit mehr Komfort mit dem Simulog der Firma
Leybold aufgebaut werden.
Dann denke ich noch an die Basteleien mit dem 7474 :-).
Zählspiel top
Das Zweiersystem ist Unterrichtsstoff der Klasse 5.
Da empfehle ich ein Zählspiel, das dem Bewegungsdrang der Schüler
in diesem Alter entgegen kommt.
... ... |
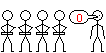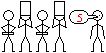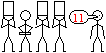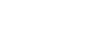Fünf Schüler dürfen nach vorne kommen, vier Schüler
bringen zur Anzeige von 0 und 1 ein Heft mit, ein Schüler zählt
laut. Haben die Schüler die ersten 15 Zahlen in Dualschreibweise vor
sich, so ist das Zählen einfach. Sie heben das Heft bei 1 und halten
es waagerecht bei 0. Das ist aber nur eine Vorübung. |
Sie können auch rein mechanisch vorgehen.
>Der Schüler auf dem Einerplatz rechts hebt und senkt sein Heft
gleichmäßig.
>Der Zweier daneben achtet nur auf den Einer. Wenn dieser sein Heft
senkt, muss er aktiv werden. Entweder hebt er sein Heft oder senkt es.
>Der Vierer achtet wieder nur auf den Zweier und folgt ihm wie der
Zweier dem Einer. Wenn der Zweier sein Heft senkt, hebt oder senkt er sein
Heft.
>Der Achter achtet auf den Vierer.
Betrachtet man einen Schüler isoliert, so hebt jeder sein Heft
in gleichen Zeitabständen, allerdings mit unterschiedlicher Frequenz.
Mit diesem Spiel gewinnt man eine neue Sicht des Zweiersystems.
Dualzahlen? top
Ich hatte die Absicht, diese Seite "Dualzahlen" zu nennen. In den Schullehrbüchern
der Mathematik wird dieser Name schon seit längerer Zeit nicht mehr
verwendet. Der Hintergrund ist, dass die Lehrbuchverfasser streng
zwischen einer
Zahl und der Darstellung einer Zahl unterscheiden.
Somit sind Ausdrücke wie Dezimalzahl, römische Zahl, gemischte
Zahl und eben Dualzahl getilgt. Unter einer Zahl versteht man nur die Zahl
an sich wie die natürliche Zahl, die rationale Zahl, die negative
Zahl usw..
Daran möchte ich mich halten, auch wenn ich persönlich das
nicht so eng sehe. Leider gibt es an Stelle der Dualzahl oder Computerzahl
keinen ebenso griffigen Namen.
Graphen top
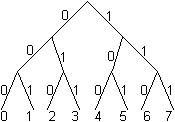
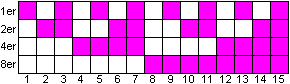
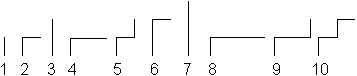
Weitere Informationen über Zahlen im Zweiersystem findet man auf meiner
Seite Tetraden.
Die Abessinische Bauernmultiplikation wird auf meiner Seite Multiplikation
mehrstelliger Zahlen besprochen.
Zweiersystem im Internet top
Deutsch
Arndt Brünner
Umrechnung
von Zahlensystemen
Daniel Kastenholz
Das Binärsystem
Wikipedia
Dualsystem, Dezimalsystem,
Stellenwertsystem,
Zahlbasiswechsel,
Rationale
Zahl
Englisch
History of the Binary System
Eric W. Weisstein (MathWorld)
Binary
Wikipedia
Binary
numeral system
Referenzen top
(1) Heinrich Behnke (u.a.): Mathematik 1, DAS FISCHER LEXIKON, Frankfurt
am Main, 1964
(2) Werner Burau: Elementare Zahlentheorie, Stuttgart
(3) LS 5, Ernst Klett Schulbuchverlag 1993 [ISBN 3-12-730700-4]
(4) LS 6, Ernst Klett Schulbuchverlag 1994 [ISBN 3-12-730710-1]
(5) D.E. Knuth: Volume 2 Seminumerical Algorithms, Third Edition (Reading,
Massachusetts: Addison-Wesley, 1997), xiv+762pp [ISBN 0-201-89684-] Chapter
4: Arithmetic
Feedback: Emailadresse auf
meiner Hauptseite
Diese
Seite ist bald auch in Englisch vorhanden.
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2006 Jürgen Köller
top |
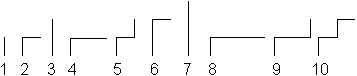
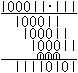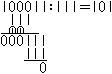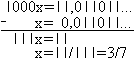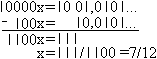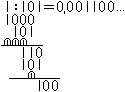
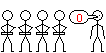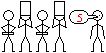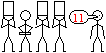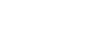