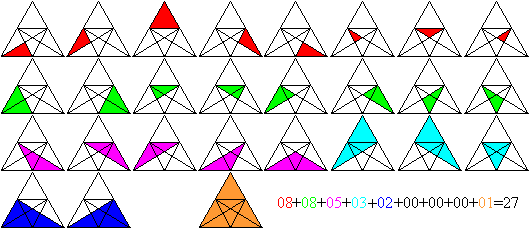|
Figuren in einer Figur zählen
|
Was heißt "Figuren in einer Figur zählen"?
top
... ... ... |
Das erklärt man am besten an einem Beispiel:
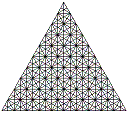
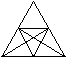
Gegeben ist eine komplexe Figur, zum Beispiel ein gleichseitiges
Dreieck, in das die Mittellinien und zwei Höhen eingezeichnet sind.
Die Aufgabe besteht darin, alle Dreiecke zu zählen,
die in der Figur vorkommen. |
Von Problemen dieser Art soll diese
Seite handeln.
Die Aufgaben sind in rot
durchnummeriert. Die Lösungen stehen erst am Ende dieser Seite.
Dreiecke
zählentop
... ... ... |
1) Wie viele Dreiecke
enthält die Figur?
 |
Die Figur ist achsensymmetrisch
bezüglich der Vertikalen durch die Mitte.
|
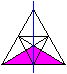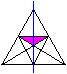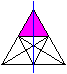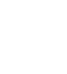
Damit treten die meisten Dreiecke
paarweise auf.
Aber fünf Dreiecke sind selbst
zu der Achse symmetrisch und haben keinen Partner (links). |
Die anderen Dreiecke erscheinen zweimal.
Folglich muss die Gesamtzahl der Dreiecke ein ungerade Zahl sein.
Will man jetzt die Dreiecke zählen,
kann man sich nach der Anzahl der Dreiecke richten, aus denen ein
Dreieck besteht. Man erfasst zuerst alle Einzeldreiecke, dann die Dreiecke,
die von zwei Dreiecken gebildet werden. Weiter gibt es noch Dreiecke, die
sich aus drei oder vier Dreiecken zusammensetzen. Dann kommt noch das Dreieck
selbst.
Weitere Aufgaben:
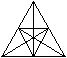
2)Wie viele Dreiecke?
|
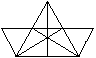
3)Wie viele Dreiecke?
|
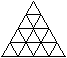
4)Wie viele Dreiecke?
|
Vierecke zählen
top
...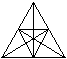 ... ... |
Zeichnet man in das Dreieck alle Mittellinien und Höhen
ein, so entsteht die Figur links.
5) Die Aufgabe besteht
darin, alle Vierecke, die in der Figur versteckt sind, zu finden.
Rechts ist ein Viereck als Beispiel angegeben. |
....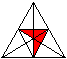 ... ...
|
Weitere Aufgaben:

6) Wie viele Vierecke?
|

7)Wie viele Parallelogramme?
|
Dreiecke
im n-ten Dreieck zählen top
Dieses ist eine Verallgemeinerung. Es stellt sich die
Frage, wie viele Dreiecke in der n-ten Figur gezählt werden können.
8)
...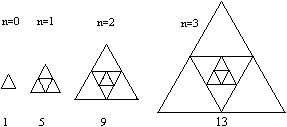 ... ... |
Diese Aufgabe ist leicht. Mit jeder neuen Figur kommen
4 Dreiecke hinzu. |
Weitere Aufgaben, die es in sich haben.
Problem 9:
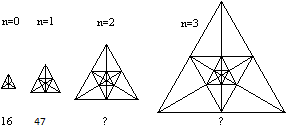
|
Problem 10:
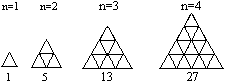
|
Dreiecke
und Vierecke aus Münzen top
Es gibt eine schöne Variation der bisher besprochenen
Aufgaben. Man gibt ein Gitter vor und soll Dreiecke oder Vierecke finden,
deren Eckpunkte gleichzeitig Gitterpunkte sind. Diese Aufgaben bekommen
eine gefälligere Form, wenn man die Gitter durch Kreise festlegt.
Die Kreise können zum Beispiel Münzen oder Spielmarken sein.
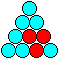
Man kann aus zehn Münzen ein Dreieck legen.
...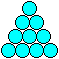 ... ... |
Innerhalb der Figur bilden drei Münzen kleinere
gleichseitige Dreiecke.
11) Wie viele gleichseitige
Dreiecke gibt es, wenn man das Ausgangsdreieck mitzählt?
Rechts findet man ein Beispiel! |
... ... ... |
[Quelle: 2, Seite 142]
... |
12)Wie viele Quadrate
enthält die Figur? Rechts findet man ein Beispiel! |

|
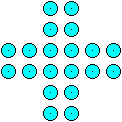
13) 20-Spielmarken-Problem:
... ... ...
|
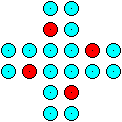
20 Spielmarken werden zu einem Kreuz gelegt.
Wie viele unterschiedliche Quadrate mit jeweils vier Spielmarken
in den Ecken kann man in der Figur entdecken?
Rechts findet man ein Beispiel. |
... ... ... |
Diese Aufgabe erschien zum ersten Mal im Buch "Angelo Lewis:
Puzzles Old and New (1893)" und wurde von Gardner aufgegriffen [Quelle:
1, Seite 234f. und 241f.].
Figuren
in einer Figur zählen im Internet top
Deutsch
Jonas Sandrock
Dreiecke
zählen
n-tv.de
Das
Netz ist verzweifelt. - Finden Sie alle Dreiecke?
Englisch
A. Bogomolny (cut-the-knot)
Counting
Triangles
Eric W. Weisstein (MathWorld)
Triangle
Tiling
Frank Buß
Triangles
Challenge
Jim Wilson
Count
the Triangles -- I, Count
the Triangles -- II, Count
the Triangles -- III
Steven E. Sommars, Tim Sommars
The
Number of Triangles Formed by Intersecting Diagonals of a Regular Polygon
Torsten Sillke
grid-triangles,
grid-squares
Referenzen
top
(1) Martin Gardner: Mathematischer Karneval, Ullstein,
Frankfurt a.M.1977 (ISBN 3 550 07675 4)
(2) Martin Gardner: Mathematischer Zirkus, Berlin 1988
(ISBN 3550076924)
Lösungen
top
...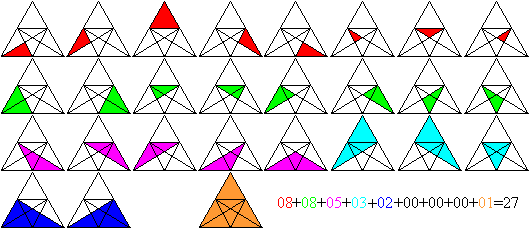
Die erste Figur dieser Seite ist
in 8 Dreiecke (und 1 Viereck) zerlegt. Es gibt 8 Einzeldreiecke,
8 Dreiecke aus 2 Figuren, 5 Dreiecke aus 3 Figuren, 3 Dreiecke aus 4 Figuren,
2 Dreiecke aus 5 Figuren und das große Dreieck selbst aus 9 Figuren.
Das kann man notieren mit: 01)
08+08+05+03+02+00+00+00+01=27 Dreiecke.
In dieser Form werden die übrigen Lösungen
notiert, bei denen es um Dreiecke oder Vierecke geht.
02) 12+12+06+09+00+07+00+00+00+00+00+00+01=47
Dreiecke
03) 10+05+06+04+02+00+00+01=28
Dreiecke
04) 16+00+00+07+00+00+00+00+03+00+00+00+00+00+00+01=27
Dreiecke
05) 00+03+06+06+12+00+00+06+00+03=36
Vierecke
06) 00+06+04+07+02+02+02+01=24
Vierecke
07) 00+18+00+18+00+06+00+03=45
Parallelogramme
08) 4n+1
09)
31n+16 (Quelle: Torsten Sillke)
10) n(n+2)(2n+1)/8 für
n gerade, [n(n+2)(2n+1)-1]/8 für n ungerade
(Quelle: Torsten Sillke)
Die Lösungen der Figuren aus Kreisen werden als
"animated Gifs" oder auf deutsch "Zappelbilder" wiedergegeben.
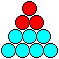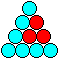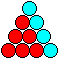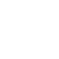
11) 15 Dreiecke
|

12) 20 Quadrate
|
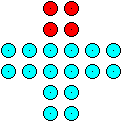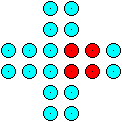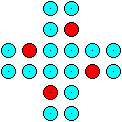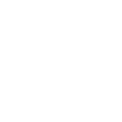
13) 21 Quadrate
|
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2003 Jürgen Köller
top |
 ...
...



 ...
... ...
...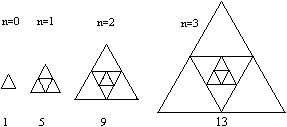 ...
...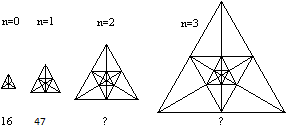
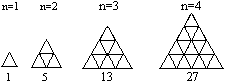
 ...
... ...
...

 ...
... ...
...