|
Was sind Kolams, was sind Sona?
Kolams sind indische Bodenmalereien; Sona (Einzahl Lusona)
sind afrikanische Sandmalereien.
Ihnen ist nur gemeinsam, dass man Punktmuster als Merkhilfe
vorgibt und dann um die Punkte herum Linien zieht, so dass jeder Punkt
eingekreist wird. Es entstehen ansehnliche symmetrische Figuren in großer
Vielfalt.
Einen Eindruck von Kolams und Sona erhält
man, wenn man sich die ersten beiden Youtube-Videos in der Linkliste unten
ansieht.
Kolams und Sona sind Gegenstand
der Ethnomathematik. Am Ende dieser Webseite gibt es dazu Links.
Beispiel eines Kolams, Beispiel
eines Lusona
Kolams top
Hintergrund
Ein Kolam ist eine südindische Bodenmalerei.
In bestimmten Regionen in Südindien schmücken
Frauen täglich die Böden vor den Häusern mit kunstvollen,
drehsymmetrischen Figuren. Sie zeichnen dazu mit Reismehl Punktmuster als
Merkhilfe und dann Linien um die Punkte herum. Dazu lassen sie mit Geschick
Pulver zwischen Zeigefinger und Mittelfinger rieseln und portionieren mit
dem Daumen.
Die oft komplizierten Muster werden in einer Familie
von Generation zu Generation weiter gegeben und haben einen religiösen
Hintergrund.
Diese "Linien-Kolams" heißen auf der englischen
Wikipedia-Seite stroke kolams, in Tamil neli kolam, kambi kolam oder sikku
kolam.
In anderen Regionen verzichtet
man meist auf Punktgitter und Linien. Stattdessen werden farbige Flächen
oder Blumenteppiche angelegt. Reismehl wird durch Steinpulver oder Kreidepulver
ersetzt, oft zusammen mit natürlichen oder synthetischen Farbpulvern.
Die immer drehsymmetrischen Bilder werden zusammen mit den Linien-Kolams
auf Feiern, auf Festivals, in Wettbewerben und im Internet dargeboten.
Einfaches
Beispiel
...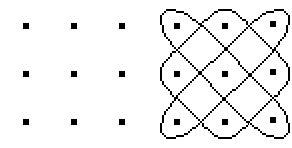 ... ... |
Gibt man neun Punkte in Quadratform vor, könnte
ein 3x3-Kolam so aussehen. |
... ... ... |
Kolams werden durch geschlossene, übergreifende
Linien erzeugt.
In diesem Falle entsteht die Figur aus den drei Randkurven
der gelben Flächenstücke. |
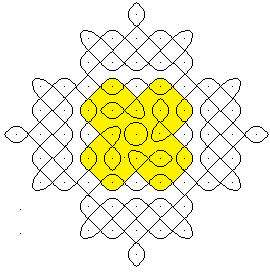
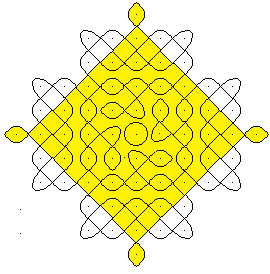
Beispiel
eines Kolams
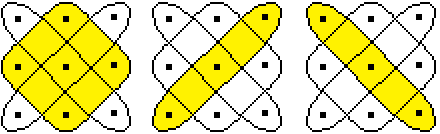
Dieses Kolam wird durch sieben
geschlossene Kurven erzeugt, markiert durch die Linien in Rot (4x), Grün,
Blau und Violett.
Den Aufbau des Kolams erkennt
man durch Gelbfärbungen besser.
- Da sind vier Außen-Figuren und ein zentraler
Kreis.
- In der Mitte liegt ein abgerundetes Kreuz.
- Ein Quadrat mit Zipfeln umschließt die Figur.
Mehrere geschlossene Linien, das ist typisch für Kolams,
wenn sie auch manchmal mit einer geschlossenen Linie auskommen.
Sona top
Hintergrund
Sona sind traditionelle Zeichnungen mancher Bantu-Völker
wie der Chokwe in einem Gebiet von Angola und Sambia im südlichen
Afrika.
Erzähler zeichnen Sona mit den Fingern in den glatt
gestrichenen Sand, während sie dazu eine Geschichte erzählen.
Ohne den Finger abzusetzen wird eine geschlossene Linie gezogen.
Die Linie führt um Punkte eines vorher festgelegten Musters herum,
kreuzt sich immer wieder und kehrt schließlich zum Anfangspunkt zurück.
Die Zeichnungen illustrieren die Geschichten.
Einfaches
Beispiel
Die Figur zu einem 4x3-Punktegitter
ist ein Lusona. D.h., sie besteht also aus einer geschlossenen Linie ohne
Anfang und Ende.
Da die Sona Geschichten ergänzen,
stellen sie oft Tiere dar.
Antilope
...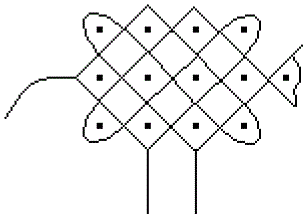 ... ... |
Das kompakte Lusona wird zu einer Antilope.
Die Zeichnung ist nicht ohne Witz. |
Leopard
...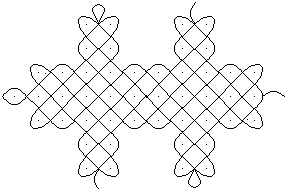 |
Das Bild zeigt einen Leoparden mit ausgestreckten Tatzen,
links der kleine Kopf, rechts das Schwänzchen.
Genauer: In der Zeichnung sind auch zwei Junge zu erkennen.
Sie liegen nebenander und entgegengesetzt.
|
Quelle (1)
Drei
Vögel
...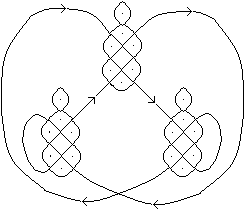 ... ... |
Es gibt auch Sona, bei denen eine Figur mehrmals auftritt.
Sie werden so verbunden, dass eine geschlossene Linie beibehalten wird.
Hier sind es drei Vögel, in meiner Vorlage sind es
zehn (!). |
Quelle (2)
Eine
Fabel
...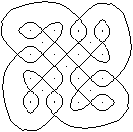 ... ... |
Das nebenstehende Lusona wird auch mit einer geschlossene
Linie gezeichnet.
Vier fast gleiche Figuren werden miteinander verknüpft.
Die abstrakte Figur wird lebendig, wenn man die Fabel
kennt, die während des Zeichnens erzählt wird. |
...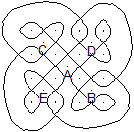 ... ... |
"Sambálu, das Kaninchen
(Punkt B), entdeckt eine Salzmine (Punkt A). Sofort fordern der Löwe
(Punkt C), der Jaguar (Punkt D) und die Hyäne (Punkt E) den Besitz,
indem sie die Rechte des Stärkeren geltend machen. Das Kaninchen,
das die unantastbaren Rechte der Schwachen bekräftigt, baut daraufhin
schnell einen Zaun, um die Mine vor allen Eindringlingen fern zu halten.
Man beachte, dass man nur von B
aus zu Punkt A gelangen kann, ohne die Linie, die den Zaun darstellt, zu
überschreiten." |
Quelle (3)
Ausnahmsweise, wenn es die
Geschichte erfordert, bestehen Sona aus mehreren geschlossenen Linien.
Trotzdem heißen auf dieser Seite die Figuren der
Einfachheit halber Sona, wenn sie aus einer geschlossen Linie entstehen.
Etwas Mathematik top
Spiegelmodell
...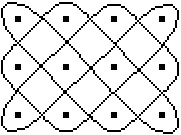 |
An Hand dieses 4x3-Lusona soll beschrieben werden,
wie die Figur an Hand einer Modellvorstellung "mathematisiert"
wird. .................... |
...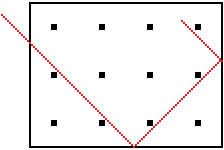 ... ... |
Man legt ein Rechteck um die 4x3 Punkte und stellt sich
vor, dass das Rechteck innen verspiegelt ist. Schickt man z.B. von oben
links einen Lichtstrahl in das Rechteck, so wird er vielfach reflektiert
und beschreibt einen Weg wie links angefangen.
Der eingezeichnete Strahl ist nicht erlaubt. Durch Gitter
wird der Weg gesteuert. |
... ... ... |
Es wird ein Gitter in das Rechteck gelegt.................................................................................. |
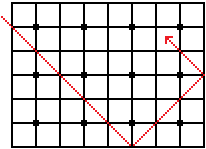 ... ... |
Dann wird ein Lichtstrahl so in das Rechteck geschickt,
dass er sich seinen Weg genau zwischen den vorgebenen Punkten bahnt. |
...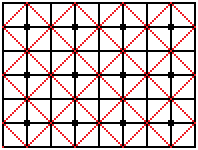 ... ... |
Schließlich gelangt er zum Ausgangspunkt zurück;
er durchquert alle Quadrate auf Diagonalen.
Zurück bleibt ein Gitter aus auf der Spitze stehenden
Quadraten. |
...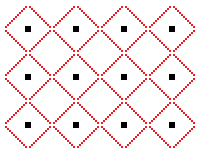 ... ... |
Das schwarze Gittter wird gelöscht........................................................................................... |
...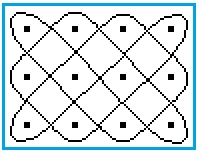 ... ... |
Man erkennt in dem roten Gitter aus Lichtstrahlen unschwer
das 4x3-Lusona.
Die Rundungen der Begrenzungslinie kann man dadurch erklären,
dass die Wände des Rechtecks als Spiegel so wirken........................................................ |
Erste
Regel
Es stellt sich die Frage, welche rechteckigen Figuren
m*n ein Lusona sind.
Dazu vier Beispiele:
...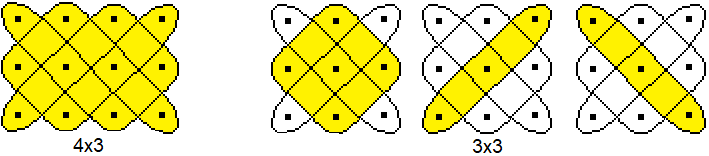
...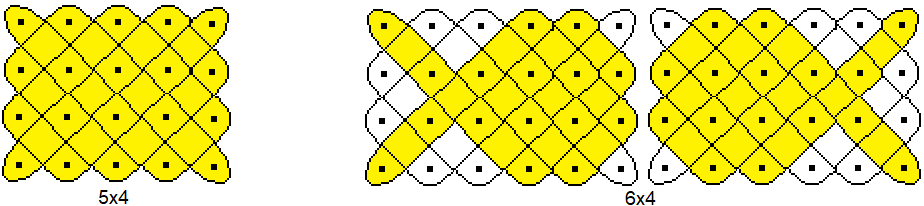
Diese vier Beispiele veranschaulichen
die folgende erste Regel.
- Eine geschlossene Linie ergibt sich nur, wenn
m und n teilerfremd sind.
- Sind mehrere geschlossenen Linien nötig, um die
Figur zu erzeugen, so ist die Anzahl der Kurven gleich dem größten,
gemeinsamen Teiler.
Die Rechtecke zur Leopardenfamilie
haben die Daten 3x10 und 2x3, ihre Maßzahlen sind teilerfremd.
... |
... ... ... |
Die Rechtecke überlappen sich so, dass sie zusammen
weiter durch eine geschlossene Linie erzeugt werden. |
Innere
zweiseitige Spiegel
... |
Die kompakten Sona werden interessanter, wenn man im
Inneren Muster erzeugt. |
... ... ... |
Im einfachsten Fall löst man eine Kreuzung auf und
ersetzt die Ecken durch Rundungen.
Das kann man im Spiegelmodell so erklären, dass man
auf eine Kreuzung einen zweiseitigen Spiegel stellt.
|
...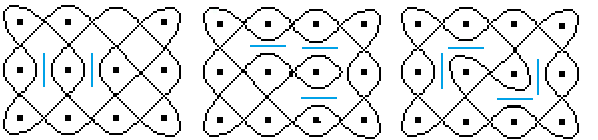 ... ... |
Man kann auch mehrere Spiegel ins Innere stellen. |
Mit dem Einsetzen eines Spiegels
ist eine Figur entstanden, die nicht mehr durch eine geschlossene Linie
entsteht.
...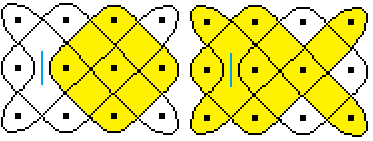 ... ... |
Man benötigt zwei geschlossene Linien, um die Figur
zu erfassen.........,,.,...................... |
...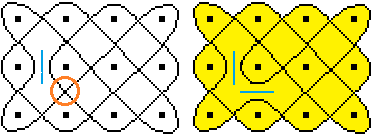 ... ... |
Aus dieser Figur kann man übrigens durch Auflösen
einer Kreuzung, in der sich die beiden verschiedenen Linien treffen, wieder
ein Lusona erzeugen. |
Zweite
Regel
Für m*n-Sonas mit einem Innenspiegels gibt es eine
einfache Regel.
Dazu muss zum 4x3-Lusona ein Muster aus dunklen und hellen
Feldern ermittelt werden.
...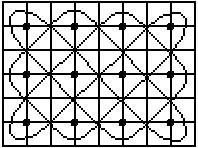 ... ... |
Man legt auf das 4x3-Lusona das Gitter.................................................................. |
...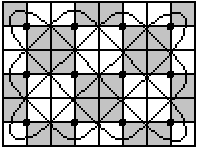 ... ... |
Man kommt zu einem Muster, wenn man die Linie verfolgt
und dabei jedes zweite Quadrat grau färbt.
Färbt man die linke obere Ecke grau, dann geht man
zwei Quadrate nach rechts und ein Quadrat nach unten. Dieses Quadrat wird
wieder grau und so fort. |
...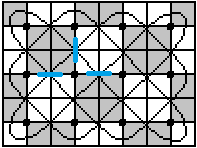 ... ... |
Die zweite Regel besagt, dass immer da, wo 2x2-Quadrate
aneinanderstoßen, ein Spiegel stehen kann.
Das sind die drei Einzelspiegel und aus Symmetriegründen
kommen noch vier dazu.
Das wird durch die Untersuchung der 42 Figuren im nächstenl
Kapitel durch die ersten drei Sona bestätigt. |
Ein
anderes Beispiel, das 5*4-Lusona
...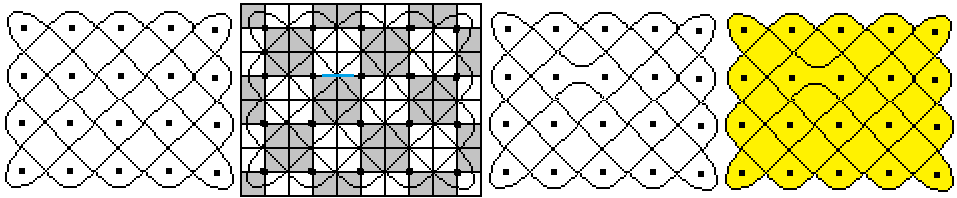
Von
Lusona zur Matrix
... ... ... |
...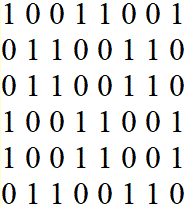 ... ... |
Schreibt man an Stelle der dunklen Felder eine Eins und
der hellen Felder eine Null, so erhält man eine Matrix aus Nullen
und Einsen.
Sie kann einer 4x3-Figur zugeordnet werden, und sie wird
durch die Matrix eindeutig beschrieben.
Umgekehrt kann man neue Muster aus 0 und 1 entwerfen und
zu neuen Sona gelangen. |
Auf
der Suche nach Sona top
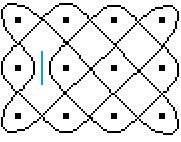
Frage: Wo müssen beim 4x3-Kolam die Doppelspiegel
im Inneren stehen, damit die Figur ein Lusona bleibt?
Dazu werden alle möglichen Positionen von bis zu
fünf Spiegeln durchgespielt.
...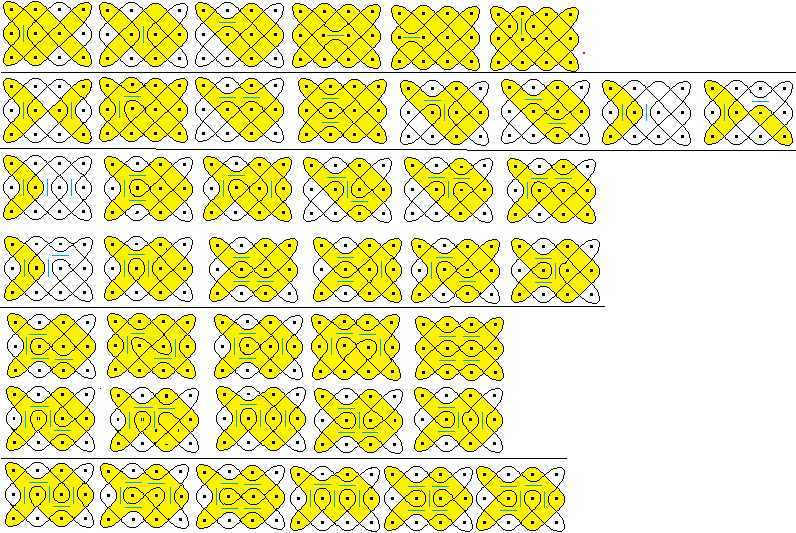
Ergebnis: Unter den 42 untersuchten Figuren sind acht
ein Lusona.
Frage: Wo müssen beim
3x3-Kolam die Doppelspiegel (blau) innen und am Rande stehen, damit die
Figur ein Lusona wird?
...
Ergebnis: Es gibt unter den Komas 36 Sona, davon sind
neun symmetrisch.
...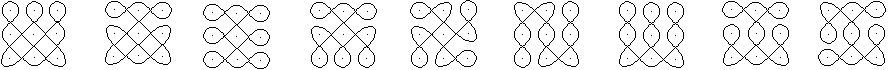
Frage: Wie gelangt man zum
folgenden Kolam aus fünf geschlossenen Kurven?
...
...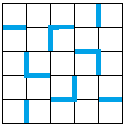 |
Man entwirft mit Kugelschreiber auf kariertem Papier
eine punktsymmetrische Figur in der Hoffnung, dass daraus ein ansehnliches
Kolam entsteht. Man zeichnet es - wie im nächsten Kapitel beschrieben
- mit MS-Paint oder einem Online-Programm. |
...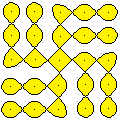 |
Man findet auch Sonas................................................................................................................................... |
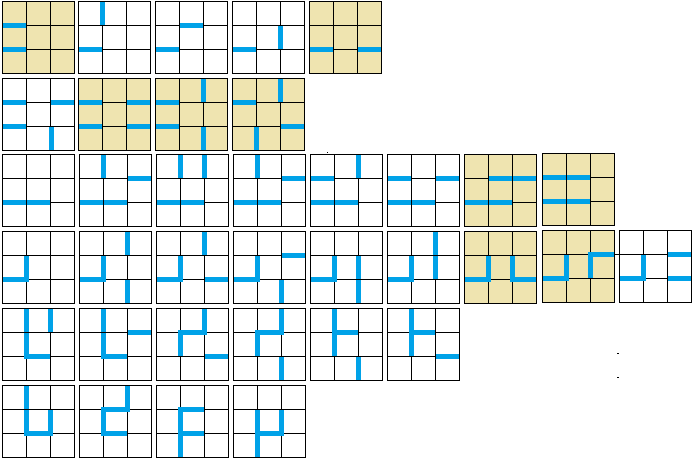
Zeichenübungen
top
Fünf Grundfiguren
Oben steht, dass Kolams entstehen,
wenn man um Punkte herum Linien zeichnet.
Gibt man ein Feld von 2x2 Punkten
vor, so gibt es viele Möglichkeiten Punkte zu umkreisen.
...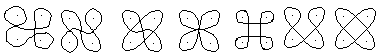
Die Kolams als Gegenstand der Mathematik sind aus den
folgenden Grundfiguren zusammengesetzt.
...
Damit fallen die ersten vier Figuren weg. Nur die drei
nächsten Figuren bezeichnet man als Kolams.
Streng genommen muss in der fünften Figur ein Punkt
in der Mitte stehen.
So
wie die Mandalas fernöstlicher Kulturen bieten sich auch die Linien-Kolams
für eigene Tätigkeiten an.
Zeichnen mit Kugelschreiber und
Papier
Gibt man z.B. ein Punktmuster 3x2 vor und will Kolams
oder gar Sona zeichnen, so wählt man an besten diesen Weg.
- Man zeichnet ein Rechteck 3x2 and wählt an passenden
Stellen Doppelspiegel.
- Dann skizziert man die Kolams. Dabei tut man sich schwer,
da man die fünf Grundfiguren im Kopf haben muss.
- Dann werden die Skizzen in eine Reinzeichnung übertragen.
...Dabei benutzt man MS-Paint
oder das Online-Programm, die unten beschrieben werden.
...
Zeichnen
mit MS-Paint
Die Zeichnungen auf dieser Webseite wurden mit dem Zeichenprogramm
MS-Paint erstellt.
Es steht jedem zur Verfügung, der im Internet Windows
benutzt.
...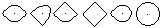 ... ... |
Die Figuren werden, wie oben schon angegeben, aus fünf
Bausteinen zusammengesetzt.
Es kommt noch ein Kreis hinzu. |
Ich
zeige als Anregung für eigene Tätigkeiten zwei Bilderfolgen.
...
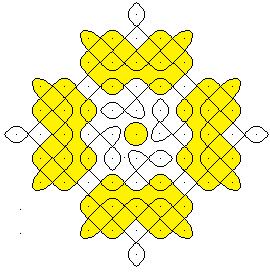
Man kann die Kolams färben.
...
Zeichnen
mit einem Programm
Im Internet steht ein Programm bereit, mit dem man leicht
Kolams zeichnen kann.
Man gelangt in das Online-Programm, indem man es in der
Linkliste unten mit dem Namen Forkphorus aufruft.
Die Benutzeroberfläche ist übersichtlich. Rechts
steht das Werkzeug, links die Zeichenfläche für maximal 5x5-Kolams.
Oben stehen die sechs Grundfiguren bereit. Man holt eine Figur auf die
Zeichenfläche, wenn man sie und dann das Zielquadrat antippt. Für
das Drehen und Löschen der Figur gibt es Felder. Mit dem Feld unten
rechts löscht man die Zeichnung. Das Feld unten links ist bei mir
ohne Wirkung.
Das Programm half, unter
den 3x3-Kolams im vorigen Kapitel die Sona zu finden. Wenn man die kompakte
3x3-Figur vorgibt, kann man alle Kolams "erzeugen", indem man passende
Grundfiguren dreht. Man erkennt die Lage der Doppelspiegel als Lücken
und kann Sonas ausmachen, auch wenn die Formen nicht stimmen.
Vorschlag
Eine vielleicht offene Frage ist, wie viele Kolams und
dann Sona es zu den kompakten, relativ einfachen 3x2- und 4x2-Figuren gibt.
Dazu muss man also systematisch nach den möglichen
Stellungen der Doppelspiegel mit Hilfe von Notizen auf kariertem Papier
suchen.
In einem zweiten Schritt erkennt man die Sonas mit Hilfe
des Online-Programms.
Kolam-Legespiel
Klebt man die Grundfiguren auf
Quadrate aus Pappe, so erhält man eine Legespiel.
...
Verschiedenes
top
Paulus Gerdes
Beim Recherchieren im Internet erkennt man, dass die
Lusona-Forschung durch den Wissenschaftler Paul Gerdes begründet und
vorangetrieben wurde. Er verfasste zu diesem Thema zahlreiche Schriften
und sammelte um sich viele Schüler, die sich mit Lusona befassten.
Er war Holländer, ab 1976 Professor der Mathematik
in Mosambik und nahm dort auch die Staatsbürgerschaft an.
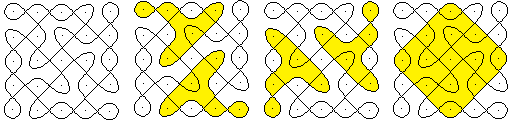
Keltische
Knoten
Aus dem 3x3-Kolam und dem 4x3-Lusona
werden keltische Knoten, wenn man die Linien dicker wählt und längs
einer Linie abwechselnd Unterführungen und Brücken setzt.
Indianisches
Sandbild
... ... ... |
Sandbild der Nordamerikanischen Ureinwohner,
fixiert mit Haarfestiger,
außerhalb des Kreises vierstrahlig,
hergestellt für Touristen,
kauften wir irgendwo in der Nähe des Grand Canyon,
USA. |
Deutsche
S(tr)andmalerei
... |
 .......................... .......................... |
Springertour
...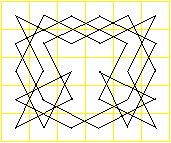 ... ... |
Bei der Springertour geht es darum, dass der Springer
sich so auf dem Schachbrett bewegen soll, dass er (auch) eine geschlossenen
Linie beschreibt. Links steht eine Lösung für das kleinere 6*5-Feld.
Mehr auf meiner Seite Haus
des Nikolaus. |
Referenzen top
(1) South African History Online (www.sahistory.org.za)
(2) https://www.zukunft-irular.de/neue-seite/ (Sona-Geometrie:
Zehn Vögel)
(3) http://www.math.buffalo.edu/mad/special/african-geometry.html
(4) https://www.researchgate.net/publication/256932750_Sona_drawings_mirror_curves_and_pattern_designs
Kolams und
Sona im Internet top
Deutsch
Alban Da Silva (Spektrum)
Mathematik
einer Südseetradition (Sandzeichnungen des südpazifischen
Archipels)
arte.tv
Kolam:
Die flüchtige Kunst der Inderinnen
Henning Krause (Spektrum)
Ethnomathematik
- dargestellt am Beispiel der Sona Geometrie
Labbé
pulli-kolams,
Was
sind Sona?
M.
Weber, A. Mischau (Mathematisches Panorama)
Mathematik
und (bzw. in) andere(n) Kulturtechniken (.pdf-Datei)
Wikipedia
Kolam,
Sona
(Mathematik), Paulus
Gerdes,
Ethnomathematik,
Sandbild,
Sandanimation
Englisch
Darrah Chavey
Mathematical
Experiments with African Sona Designs
Darrah Chavey
Constructing
Symmetric Chokwe Sand Drawings
Forkphorus
Drawing
program
Ljiljana Radovic
MIRROR
CURVES
Marcia Ascher (spektrum.de)
Ethnomathematik:
Die Kolam-Figuren Südindiens
Mattia De’ Michieli Vitturi
Sona
drawings, mirror curves and pattern designs
NN
Sona
- Sand Drawings from Africa
Paulus Gerdes
m-Canonic
mirror curves
Paulus Gerdes
Geometria
Sona de Angola Matemática duma Tradição Africana
Portugiesisch, 191 Seiten, 342 Abbildungen
Slavik Jablan, Ljiljana Radovi,
Radmila Sazdanovi Ana Zekovi
Knots
in Art
South African History Online
Sona
Patterns - Revisiting the Contributions of the People in Sub-Saharan Africa
to Modern Mathematics
Wikipedia
Kolam,
Rangoli,
Lusona,
Sandpainting,
Sand
animation, Sand
mandala,
Ethnomathematics,
Zenigata_Sunae
Youtube
Angolan
Sand Drawings
Einige Zeichnungen und Geschichten
Youtube
CHIKKU
KOLAM WITH 10-2 DOTS | HOW TO DRAW A SIKKU KOLAM | NELI KOLAM
Beispiel einer indischen Bodenmalerei
Youtube
Pongal'
theme for Chennai's Kolam and Rangoli competition
Ein Treffen der Künstlerinnen
Youtube
Kolam
designs
Riesensammlung von Videos
Schlussbemerkung top
Ein Besucher meiner Seiten, Volker Sayn, hat mich auf
die Kolams und Sona hingewiesen, die ich vorher zu meiner eigenen Verwunderung
nicht kannte. Ich habe für diese Webseite seine umfangreichen Unterlagen
vewendet und bedanke mich.
Feedback: Emailadresse auf meiner Hauptseite
Diese Seite ist auch in Englisch
vorhanden.
URL meiner Homepage:
https://www.mathematische-basteleien.de
© März 2023 Jürgen
Köller
top |






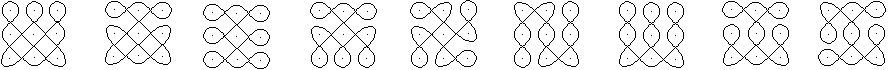






 ...
... ...
...

 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...
 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...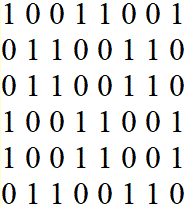 ...
...


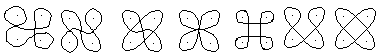


 ...
...
 ..........................
.......................... ...
...