|
Was ist ein Johnson-Körper?
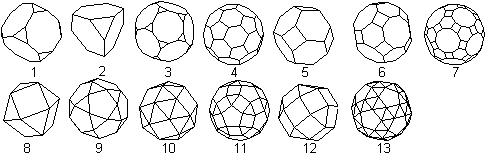
Es gibt in der Geometrie das Problem, alle konvexen Körper
zu finden, die nur von regelmäßigen Vielecken begrenzt werden.
Das Problem ist gelöst.
Es gibt die 5 platonischen
Körper und die 13 archimedischen Körper.
... |
 |
Es gibt "unendlich viele"
Prismen.
... . .
.. |
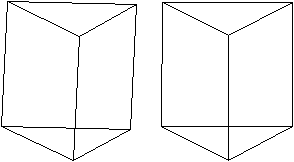
Das Prisma hat als Grund- bzw. Deckfläche ein gleichseitiges
Dreieck und als Seitenflächen Quadrate. Man stelle sich vor, das Dreieck
werde nacheinander durch ein Quadrat, ein regelmäßiges
Fünfeck, ein regelmäßiges Sechseck usw. ersetzt und die
Seitenquadrate würden beibehalten.
Dann entsteht eine unendliche Folge von Prismen, die
von regelmäßigen Vielecken begrenzt werden. |
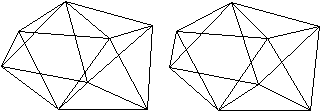
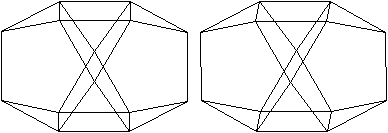
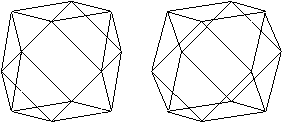
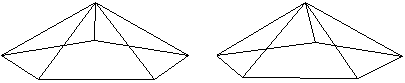
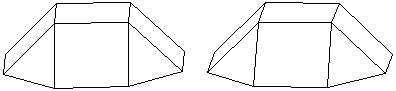
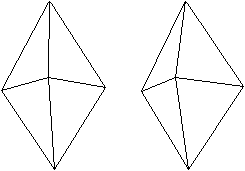
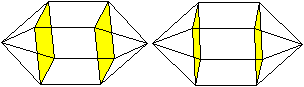
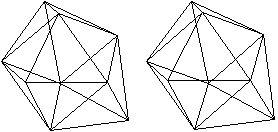
Zwei Körper aus der
Folge der n-seitigen Prismen.
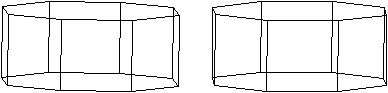
n=8
|
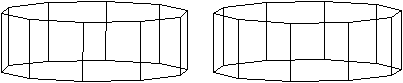
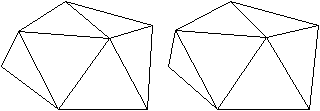
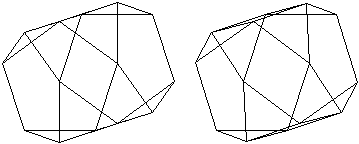
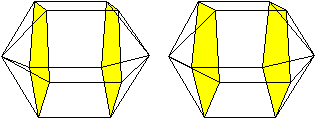
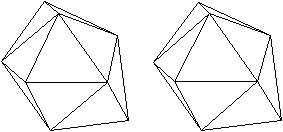
n=10
|
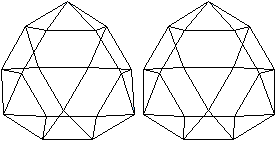
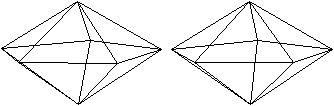
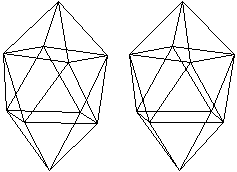
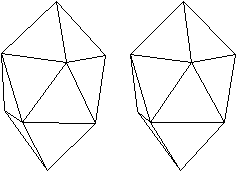
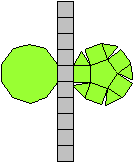
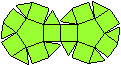
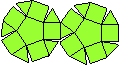
Die Bildpaare ermöglichen eine dreidimensionale Sicht
der Körper.
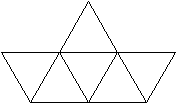
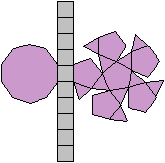
Auch für die Antiprismen
kann man eine unendliche Folge von Körpern mit regelmäßigen
Begrenzungsflächen konstruieren. Man wählt als Grund- und Deckfläche
ein Quadrat, ein regelmäßiges Fünfeck und so weiter. Die
Seitenflächen bleiben gleichseitige Dreiecke.
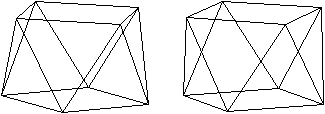
n=4
|
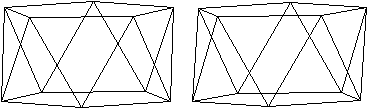
n=5
|
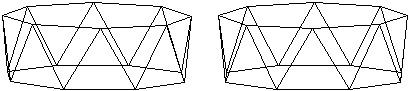
n=8
|

n=10
|
Die restlichen Körper
sind die 92 Johnson-Körper.
Der Name geht auf Norman Johnson zurück, der 1966
die Liste der 92 Körper veröffentlichte.
...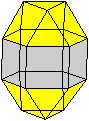 ... ... |
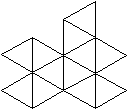
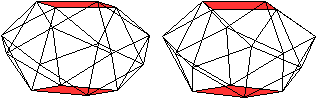
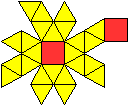
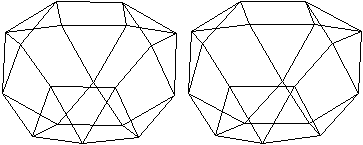
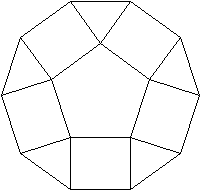
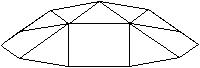
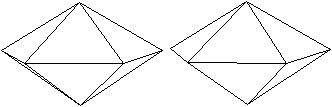
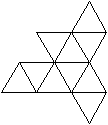
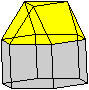
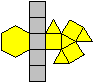
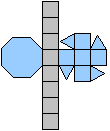
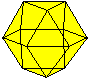
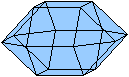
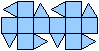
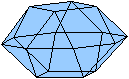
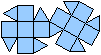
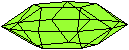
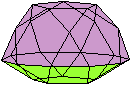
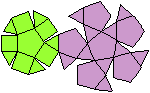
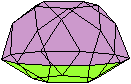
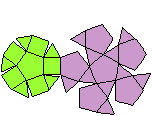
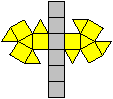
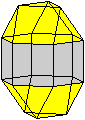
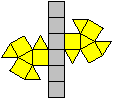
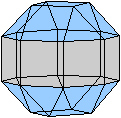
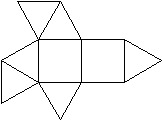
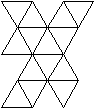
Ein Beispiel ist die verlängerte Dreiecksdoppelkuppel.
Sie ist der Johnson-Körper Nr. 35, kurz J35. |
Der Körper hat 18 Ecken, 36 Kanten, 20 Flächen
und wird gebildet von 8 Dreiecken und 12 Quadraten.
Das wird auf dieser Webseite so abgekürzt:
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (18, 36,
20, 8, 12, 0, 0, 0, 0)
Aufzählung
der Körper top
Es werden nur die Körper genannt, die auf dieser
Webseite vorkommen.
J01 Quadratpyramide
J02 Fünfeckpyramide
J03 Dreieckskuppel
J04 Quadratkuppel
J05 Fünfeckskuppel
J06 Fünfecksrotunde
J08 Verlängerte Quadratpyramide
J11 Verdreht verlängerte Fünfeckpyramide
(beschnittenes Ikosaeder)
J12 Triangulare Bipyramide
J13 Pentagonale Bipyramide
J15 Verlängerte tetragonale
Bipyramide
J16 Verlängerte pentagonale
Bipyramide
J17 Verdreht verlängerte Quadratbipyramide
J18 Verlängerte Dreieckskuppel
J19 Verlängerte Quadratkuppel
(beschnittenes kleines
Rohmbenkuboktaeder)
J20 Verlängerte Fünfeckskuppel
J21 Verlängerte Fünfecksrotunde
J22 Verdreht verlängerte Dreieckskuppel
J23 Verdreht verlängerte Quadratkuppel
J24 Verdreht verlängerte Fünfeckskuppel
J25 Verdreht verlängerte Fünfecksrotunde
J27 Dreiecksdoppelkuppel
(verdrehtes Kuboktaeder)
J28 Quadratdoppelkuppel
J29 Verdrehte Quadratdoppelkuppel
J30 Fünfecksdoppelkuppel
J31 Verdrehte Fünfecksdoppelkuppel
J32 Fünfeckskuppelrotunde
J33 verdrehte Fünfeckskuppelrotunde
J34 Fünfecksdoppelrotunde
(verdrehtes Ikosidodekaeder)
J35 Verlängerte Dreiecksdoppelkuppel
J36 Verlängerte verdrehte Dreiecksdoppelkuppel
J37 Verlängerte verdrehte Quadratsdoppelkuppel
(verdrehtes kleines
Rhombenkuboktaeder)
J38 Verlängerte Fünfecksdoppelkuppel
J39 Verlängerte verdrehte Fünfecksdoppelkuppel
J40 Verlängerte Fünfeckskuppelrotunde
J41 Verlängerte verdrehte Fünfeckskuppelrotunde
J42 Verlängerte Fünfecksdoppelrotunde
J43 Verlängerte verdrehte Fünfecksdoppelrotunde
J44 Verdreht verlängerte Dreiecksdoppelkuppel
J45 Verdreht verlängerte Quadratdoppelkuppel
J46 Verdreht verlängerte Fünfecksdoppelkuppel
J47 Verdreht verlängerte Fünfeckskuppelrotunde
J48 Verdreht verlängerte Fünfecksdoppelrotunde
J49 Erweitertes dreieckiges Prisma
J51 Dreifach erweitertes Dreiecksprisma
J58 Erweitertes Dodekaeder
J59 Doppelt erweitertes Dodekaeder (para)
J60 Doppelt erweitertes Dodekaeder (meta)
J 61 Dreifach erweitertes Dodekaeder
J62 Doppelt beschnittenes Ikosaeder (meta)
J63 Dreifach beschnittenes Ikosaeder
J64 Erweitertes dreifach beschnittenes Ikosaeder
J84 Trigondodekaeder
J85 Abgeschrägtes quadratisches
Antiprisma
J91 Bilunadoppelrotunde
J92 Dreieckshebosphenorotunde |
J01 Square pyramid
J02 Pentagonal pyramid
J03 Triangular cupola
J04 Square cupola
J05 Pentagonal cupola
J06 Pentagonal rotunda
J08 Elongated square pyramid
J11 Gyroelongated pentagonal pyramid
( diminished icosahedron)
J12 Triangular dipyramid
J13 Pentagonal dipyramid
J15 Elongated square dipyramid
J16 Elongated pentagonal dipyramid
J17 Gyroelongated square dipyramid
J18 Elongated triangular cupola
J19 Elongated square cupola
(diminished rhombicuboctahedron)
J20 Elongated pentagonal cupola
J21 Elongated pentagonal rotunda
J22 Gyroelongated triangular cupola
J23 Gyroelongated square cupola
J24 Gyroelongated pentagonal cupola
J25 Gyroelongated pentagonal rotunda
J27 Triangular orthobicupola
(gyrate cuboctahedron)
J28 Square orthobicupola
J29 Square gyrobicupola
J30 Pentagonal orthobicupola
J31 Pentagonal gyrobicupola
J32 Pentagonal orthocupolarotunda
J33 Pentagonal gyrocupolarotunda
J34 Pentagonal orthobirotunda
(gyrate icosidodecahedron)
J35 Elongated triangular orthobicupola
J36 Elongated triangular gyrobicupola
J37 Elongated square gyrobicupola
(gyrate rhombicuboctahedron)
J38 Elongated pentagonal orthobicupola
J39 Elongated pentagonal gyrobicupola
J40 Elongated pentagonal orthocupolarotunda
J41 Elongated pentagonal gyrocupolarotunda
J42 Elongated pentagonal orthobirotunda
J43 Elongated pentagonal gyrobirotunda
J44 Gyroelongated triangular bicupola
J45 Gyroelongated square bicupola
J46 Gyroelongated pentagonal bicupola
J47 Gyroelongated pentagonal cupolarotunda
J48 Gyroelongated pentagonal birotunda
J49 Augmented triangular prism
J51 Triaugmented triangular prism
J58 Augmented dodecahedron
J59 Parabiaugmented dodecahedron
J60 Metabiaugmented dodecahedron
J61 Triaugmented dodecahedron
J62 Metabidiminished icosahedron
J63 Tridiminished icosahedron
J64 Augmented tridiminished icosahedron
J84 Snub disphenoid
J85 snub square antiprism
J91 Bilunabirotunda
J92 Triangular hebesphenorotunda |
Die Körper
der Reihe nach top
J1 Quadratpyramide
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (5, 8, 5,
4, 1, 0, 0, 0, 0)
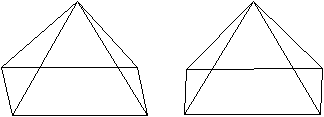
durchsichtig
|
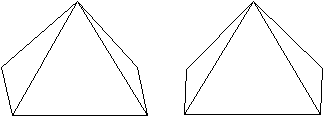
undurchsichtig
|
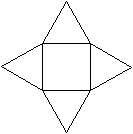
Netz
|
Das
sind vier besondere Ansichten des Körpers.
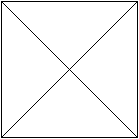
Die Grundfläche liegt
parallel zur Zeichenebene.
|
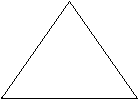
Die Grundfläche liegt
senkrecht zur Zeichenebene.
|
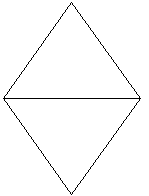
Zwei Dreiecke liegen
senkrecht zur Zeichenebene.
|
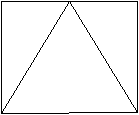
Ein Dreieck liegt
parallel zur Zeichenebene.
|
Oberfläche
und Volumen
Ist die Kantenlänge mit a gegeben, so gilt V = (1/6)sqrt(2)a³
und O = [1+sqrt(3)]a².
Die gerundeten Werte sind V = 0,24a³ und O = 2,73a².
Beziehung
zum Oktaeder
...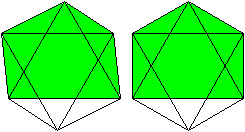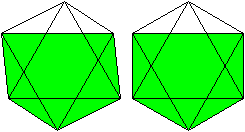 |
Ein Oktaeder
wird gebildet von zwei Quadratpyramiden. |
J2 Fünfeckpyramide
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (6,
10, 6, 5, 0, 1, 0, 0, 0)
Das
sind vier besondere Ansichten des Körpers.
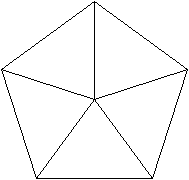
Die Grundfläche liegt
parallel zur Zeichenebene.
|
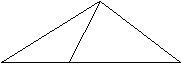
Die Grundfläche liegt
senkrecht zur Zeichenebene.
|
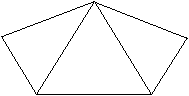
Zwei Dreiecke liegen
senkrecht zur Zeichenebene.
|
Zwei Dreiecke liegen
senkrecht zur Zeichenebene.
|
Oberfläche
und Volumen
Ist die Kantenlänge mit a gegeben, so gilt V/a³
= (1/24)sqrt[5+sqrt(5)] und O/a² = (1/4)sqrt[25+10sqrt(5)]+(5/4)sqrt(3)
Die gerundeten Werte sind V = 0,30a³ und O = 3,89a².
Beziehung
zum Ikosaeder
...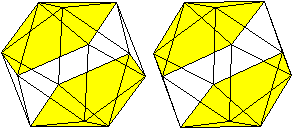 ... ...
|
Ein Ikosaeder wird gebildet von
einem fünfseitigen Antiprisma und zwei Kappen in Form von Fünfeckpyramiden. |
Was ist eine Kuppel?
...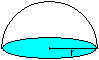 ... ... |
Im landläufigen Verständnis ist die Kuppel
eine Halbkugel, die einen Raum oben abschließt. |
In der Geometrie ist die
Kuppel eher ein von regelmäßigen Vielecken gebildeter mathematischer
Körper, der wie eine Kuppel aussieht.
... ... ... |
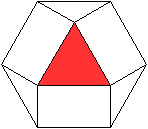
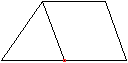
Es gibt die Dreieckskuppel, die Quadratkuppel und die
Fünfeckskuppel. Zwischen ihnen liegt ein Band aus Dreiecken und Quadraten. |
Ist die Deckfläche ein
n-Eck, so ist die Grundfläche ein (2n)-Eck.
J03 Dreieckskuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (9, 15, 8,
4, 3, 0, 1, 0, 0)
...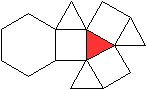 ... ... |
... ... ... |
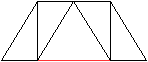
Ein Netz kann man so anlegen, dass entweder die Grundfläche
oder die Deckfläche isoliert ist. |
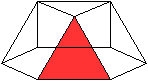
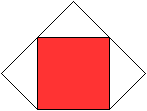
Besondere
Ansichten
Die rot gekennzeichneten Elemente liegen vorne.
Oberfläche und Volumen
Ist die Kantenlänge mit a gegeben, so gilt V = [(5/6)sqrt(2)]a³
und O = [3+(5/2)sqrt(3)]a².
Die gerundeten Werte sind V = 1,18a³ und O = 7,33a².
Beziehung
zum Kuboktaeder
... edron03.gif... edron03.gif... |
Ein Kuboktaeder wird von
zwei Dreieckskuppeln gebildet.
Dazu halbiert man in der Sechseck-Ebene.
 |
J04 Quadratkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (12, 20,
10, 4, 5, 0, 0, 1, 0)
Netze
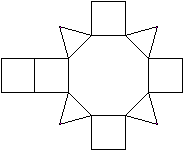
Das Quadrat ist isoliert.
|
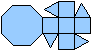
Das Achteck ist isoliert.
|
Das
sind vier besondere Ansichten des Körpers.
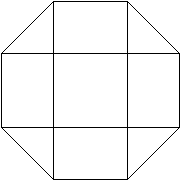
Grund- und Deckfläche liegen
parallel zur Zeichenebene.
|

Grund- und Deckfläche liegen
senkrecht zur Zeichenebene.
|
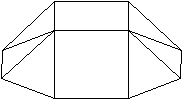
Drei Kanten liegen
übereinander.
|
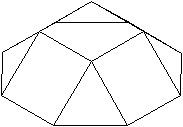
Zwei Quadrate liegen
senkrecht zur Zeichenebene.
|
Oberfläche und Volumen
Ist die Kantenlänge mit a gegeben, so gilt V = [1+(2/3)sqrt(2)]a³
und O = [7+2sqrt(2)+sqrt(3)]a².
Die gerundeten Werte sind V=1,94a³ und O=11,56a².
Beziehung
zum Rhombenkuboktaeder
...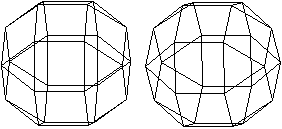 ... ... |
Das Rhombenkuboktaeder
besteht aus einem achtseitigen Prisma, auf das zwei Quadratkuppeln gesetzt
werden. |
J05 Fünfeckskuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (15, 25,
12, 5, 5, 1, 0, 0, 1)
Netze
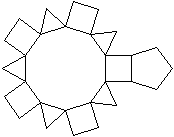
Das Fünfeck ist isoliert.
|
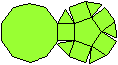
Das Zehneck ist isoliert.
|
Das
sind vier besondere Ansichten des Körpers.
Volumen
und Oberfläche
...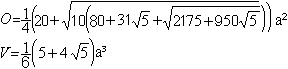 |
gerundet:
O=16,58a², V=2,32a³ |
Beziehung
zum kleinen Rhombenikosidodekaeder
...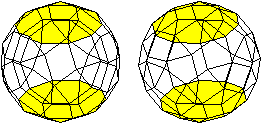 ... ... |
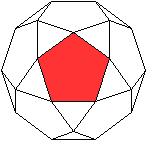
Beim kleinen
Rhombenikosidodekaeder gehört zu
jedem Fünfeck eine Fünfeckkuppel. Zwei
Kuppeln liegen sich jeweils gegenüber.
Danach besteht der Körper
aus 12 ineinander geschachtelten Fünfeckkuppeln. |
J06 Fünfecksrotunde
...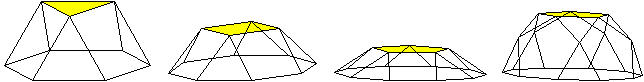
Oben wurden drei Kuppeln vorgestellt.
Die vierte Kuppel heißt wohl wegen der aufwändig gestalteten
Kuppel Rotunde, genauer Fünfecksrotunde. So
kann man zwei Kuppeln mit gleicher Deckfläche voneinander unterscheiden.
Daten: (e, k, f, A3, A4,
A5, A6, A8, A10) = (20, 35, 17, 10, 0, 6, 0, 0, 1)
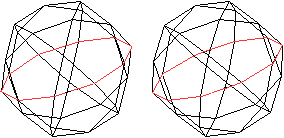
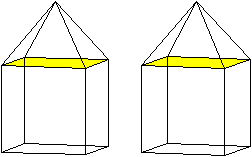
Es gibt besondere Ansichten
der Fünfecksrotunde. Die rot gezeichneten
Elemente liegen vorne.
Volumen
und Oberfläche
...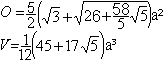 |
gerundet:
O = 22,36a², V = 6,92a³ |
Beziehung
zum Ikosidodekaeder
J08 Verlängerte Quadratpyramide
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (9, 16, 9,
4, 5, 0, 0, 0, 0)
J11 Verdreht verlängerte
Fünfeckpyramide
(e, k, f, A3, A4, A5, A6, A8, A10) = (11, 25, 16, 15,
0, 1, 0, 0, 0 )
J12 Triangulare Bipyramide
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (5, 9, 6,
6, 0, 0, 0, 0, 0)
...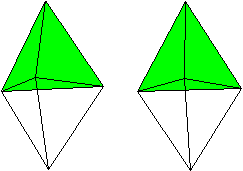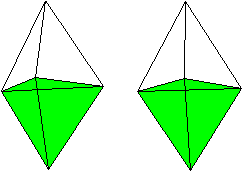 ... ... |
Der Körper entsteht, indem
man ein Tetraeder an der Grundfläche spiegelt. |
Die triangulare Bipyramide
gehört
zu den acht konvexen Deltaedern.
J13 Pentagonale Bipyramide
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (7, 15, 10,
10, 0, 0, 0, 0, 0)
...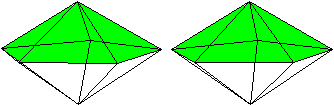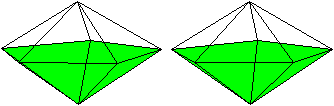 ... ... |
Der Körper entsteht, indem
man die regelmäßige fünfseitige Pyramide
an der Grundfläche spiegelt. |
Die pentagonale Bipyramide gehört zu den acht
konvexen Deltaedern.
J15 Verlängerte tetragonale
Bipyramide
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (10, 20,
12, 8, 4, 0, 0, 0, 0)
J16 Verlängerte pentagonale
Bipyramide top
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (12, 25,
15, 10, 5, 0, 0, 0, 0)
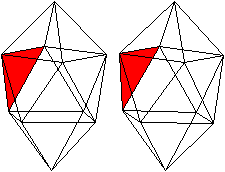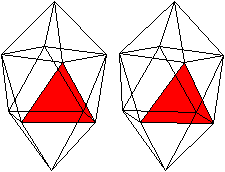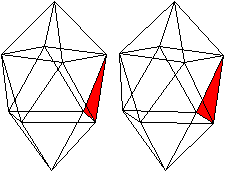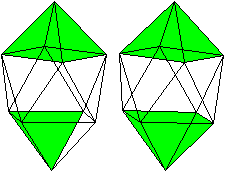
J17 Verdreht verlängerte
Quadratbipyramide
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (10, 24,
16, 16, 0, 0, 0, 0, 0)
... ... ...
|
Der Körper hat acht gleichseitige Dreiecke, die
zu einem Antiprisma gehören.
Auf das Antiprisma werden zwei quadratische Pyramiden
gesetzt. |
Die verdreht
verlängerte Quadratbipyramide gehört zu den acht konvexen
Deltaedern.
J18 Verlängerte Dreieckskuppel
top
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (15, 27,
14, 4, 9, 0, 1, 0, 0)
J19 Verlängerte Quadratkuppel
(beschnittenes kleines Rhombenkuboktaeder)
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (20, 36,
18, 4, 13, 0, 0, 1, 0)
J20 Verlängerte Fünfeckskuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (25, 45,
22, 5, 15, 1, 0, 0, 1)
J21 Verlängerte Fünfecksrotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (30, 55,
27, 10, 10, 6, 0, 0, 1)
J22 Verdreht verlängerte Dreieckskuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (15, 33,
20, 16, 3, 0, 1, 0, 0)
J23 Verdreht verlängerte Quadratkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (20, 44,
26, 20, 5, 0, 0, 1, 0)
J24 Verdreht verlängerte Fünfeckskuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (25, 55,
32, 25, 5, 1, 0, 0, 1)
J25 Verdreht verlängerte Fünfecksrotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (30, 65,
37, 30, 0, 6, 0, 0, 1)
J27 Dreiecksdoppelkuppel
(verdrehtes Kuboktaeder)
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (12, 24,
14, 8, 6, 0, 0, 0, 0)
J28 Quadratdoppelkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (16, 32,
18, 8, 10, 0, 0, 0, 0)
J29 verdrehte Quadratdoppelkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (16, 32,
18, 8, 10, 0, 0, 0, 0)
J30 Fünfecksdoppelkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (20, 40,
22, 10, 10, 2, 0, 0, 0)
J31 verdrehte Fünfecksdoppelkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (20, 40,
22, 10, 10, 2, 0, 0, 0)
J32 Fünfeckskuppelrotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (25, 50,
27, 15, 5, 7, 0, 0, 0)
J33 Verdrehte Fünfeckskuppelrotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (25, 50,
27, 15, 5, 7, 0, 0, 0)
J34 Fünfecksdoppelrotunde
(verdrehtes Ikosidodekaeder)
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (30, 60,
32, 20, 0, 12, 0, 0, 0)
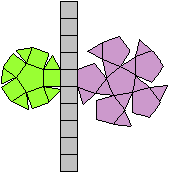
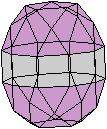
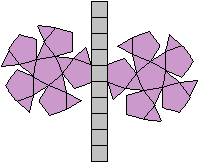
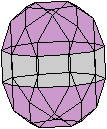
J35 Verlängerte Dreiecksdoppelkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (18, 36,
20, 8, 12, 0, 0, 0, 0)
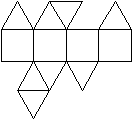
J36 Verlängerte verdrehte Dreiecksdoppelkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (18, 36,
20, 8, 12, 0, 0, 0, 0)
Die beiden Kuppeln sind gegeneinander gedreht.
J37 Verlängerte verdrehte Quadratsdoppelkuppel
(verdrehtes kleines Rhombenkuboktaeder)
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (24, 48,
26, 8, 18, 0, 0, 0, 0)
J38 Verlängerte Fünfecksdoppelkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (30, 60,
32, 10, 20, 2, 0, 0, 0 )
J39 Verlängerte verdrehte Fünfecksdoppelkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (30, 60,
32, 10, 20, 2, 0, 0, 0)
J40 Verlängerte Fünfeckskuppelrotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (35, 70,
37, 15, 15, 7, 0, 0, 0)
J41 Verlängerte verdrehte Fünfeckskuppelrotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (35, 70,
37, 15, 15, 7, 0, 0, 0 )
J42 Verlängerte Fünfecksdoppelrotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (40, 80,
42, 20, 10, 12, 0, 0, 0)
J43 Verlängerte verdrehte Fünfecksdoppelrotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (40, 80,
42, 20, 10, 12, 0, 0, 0)
J44 Verdreht verlängerte Dreiecksdoppelkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (18, 42,
26, 20, 6, 0, 0, 0, 0)
Zwischen den beiden Dreieckskuppeln liegt ein Ring aus gleichseitigen
Dreiecken.
J45 Verdreht verlängerte Quadratdoppelkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (24, 56,
34, 24, 10, 0, 0, 0, 0)
J46 Verdreht verlängerte Fünfecksdoppelkuppel
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (30, 70,
42, 30, 10, 2, 0, 0, 0)
J47 Verdreht verlängerte Fünfeckskuppelrotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (35, 80,
47, 35, 7, 0, 0, 0)
J48 Verdreht verlängerte Fünfecksdoppelrotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (40,
90, 52, 40, 0, 12, 0, 0, 0)
J49 Erweitertes dreieckiges Prisma
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (7, 13, 8,
6, 2, 0, 0, 0 ,0)
J 51 Dreifach erweitertes Dreiecksprisma
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (9, 21, 14,
14, 0, 0, 0, 0, 0)
...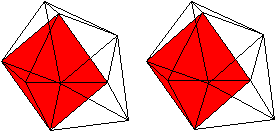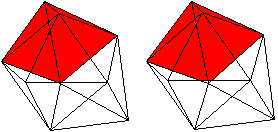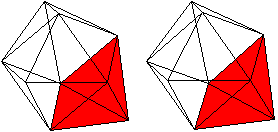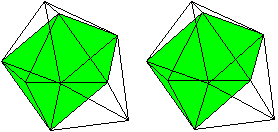 ... ... |
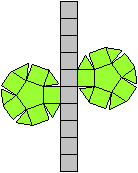
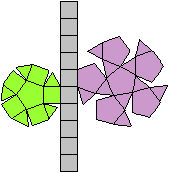
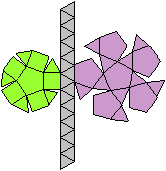
Der Körper besteht aus einem Dreiecksprisma (grün),
auf dessen Quadrate quadratische Pyramiden (rot) aufgesetzt werden. |
Das dreifach erweiterte Dreiecksprisma gehört
zu den acht konvexen Deltaedern.
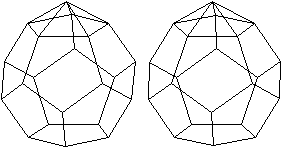
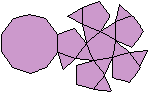
J58 Erweitertes Dodekaeder
(e, k, f, A3, A4, A5, A6, A8, A10) = (21, 35, 16, 5,
0, 11, 0, 0, 0)
... ... ... |
...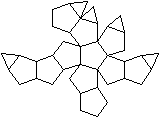 ... ... |
Dem Körper liegt ein Pentagondodekader zugrunde.
Auf eine Seitenflächen wird eine fünfseitige
Pyramide gesetzt. |
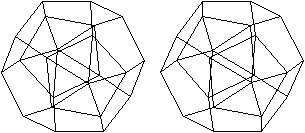
J59 Doppelt erweitertes Dodekaeder (para)
(e, k, f, A3, A4, A5, A6, A8, A10) = (22, 40, 20, 10,
0, 10, 0, 0, 0)
... ... ...
|
...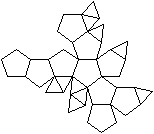 ... ... |
Dem Körper liegt ein Pentagondodekader zugrunde.
Auf zwei gegenüberliegende Seitenflächen wird
eine fünfseitige Pyramide gesetzt. |
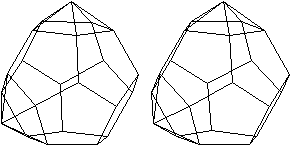
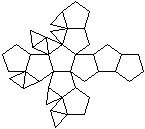
J60 Doppelt erweitertes Dodekaeder (meta)
(e, k, f, A3, A4, A5, A6, A8, A10) = (22, 40, 20, 10,
0, 10, 0, 0, 0)
... ... ...
|
... ... ...
|
Dem Körper liegt ein Pentagondodekader zugrunde.
Auf zwei nicht gegenüberliegende Seitenflächen
wird eine fünfseitige Pyramide gesetzt. |
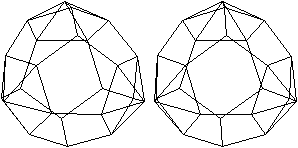
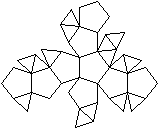
J 61 Dreifach erweitertes Dodekaeder
(e, k, f, A3, A4, A5, A6, A8, A10) = (23, 45, 24, 15,
0, 9, 0, 0, 0)
...  ... ... |
... ...
... |
Dem Körper liegt ein Pentagondodekader zugrunde.
Auf drei Seitenflächen wird eine fünfseitige
Pyramide gesetzt. |
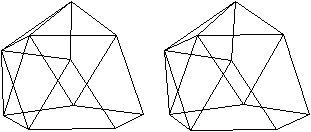
J 62 Doppelt beschnittenes Ikosaeder (meta)
(e, k, f, A3, A4, A5, A6, A8, A10) = (10, 20, 12, 10,
0, 2, 0, 0, 0)
..... |
.... .. .. |
Das Ikosaeder enthält innen 12 Fünfecke.
Man beschneidet es so, dass zwei Fünfecke außen
liegen. |
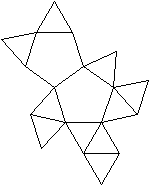
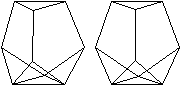
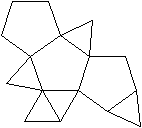
J63 Dreifach beschnittenes Ikosaeder
(e, k, f, A3, A4, A5, A6, A8, A10) = (9, 15, 8, 5, 0,
3, 0, 0, 0)
... ... ... |
... ...
... |
Das Ikosaeder enthält innen 12 Fünfecke.
Man beschneidet es so, dass drei Fünfecke außen
liegen. |
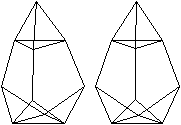
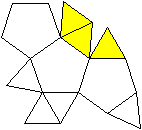
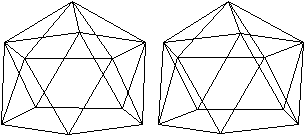
J 64 Erweitertes dreifach beschnittenes Ikosaeder
(e, k, f, A3, A4, A5, A6, A8, A10) = (10, 18, 10, 7,
0, 3, 0, 0, 0)
.. .... .... |
... ... ...
|
Auf das dreifach beschnittene Ikosaeder J63 wird ein
Tetraeder gesetzt. |
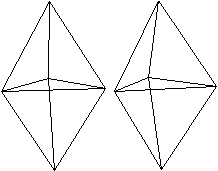
J84 Trigondodekaeder
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (8, 18, 12,
12, 0, 0, 0, 0, 0)
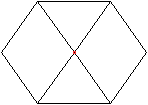
...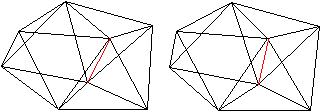 |
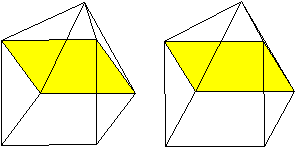
Zeichnet man eine rote Linie ein, so liegt links ein
Oktaeder, rechts lehnen sich drei Tetraeder an. Die Körper sind aber
nicht regelmäßig, sondern verbogen. |
Das Trigondodekaeder
gehört zu den acht konvexen
Deltaedern.
J85 Abgeschrägtes quadratisches
Antiprisma
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (16, 40,
26, 24, 2, 0, 0, 0, 0)
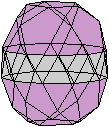
Bei diesem Körper liegt zwischen
zwei quadratischen Grundflächen ein Geflecht aus 24 gleichseitigen
Dreiecken.
Besondere Ansichten
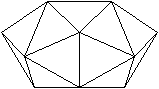
Die Quadrate erscheinen als Strecken.
|
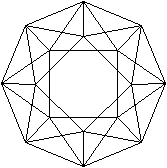
durchsichtig
|
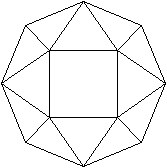
undurchsichtig
|
Die Quadrate liegen parallel zur Zeichenebene.
|
J91 Bilunadoppelrotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (14, 26,
14, 8, 2, 4, 0, 0, 0)
Zwei Ansichten
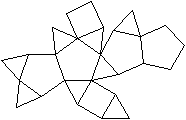
J92 Dreieckshebosphenorotunde
Daten: (e, k, f, A3, A4, A5, A6, A8, A10) = (18, 36,
20, 13, 3, 3, 1, 0, 0)
Zwei Ansichten
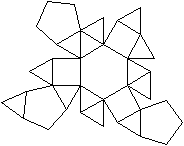
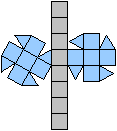
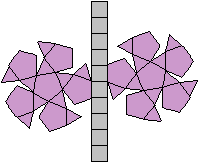
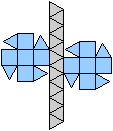
Ordnen der Kuppeln
top
Das sind noch einmal die Kuppeln, nämlich die Dreieckskuppel,
die Quadratkuppel, die Fünfeckskuppel und die
Fünfecksrotunde.
Aus ihnen bildet man etliche neue Körper.
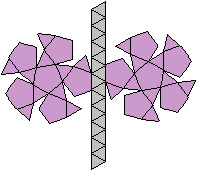
Sieben Körper gehen
aus der Dreieckskuppel hervor.
Die beiden untereinander
stehenden Körper haben das Prisma in der Mitte und die Kappen gemeinsam,
nur dass die Kappen in sich gedreht sind.
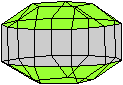
Sieben Körper gehen aus der Quadratkuppel hervor.
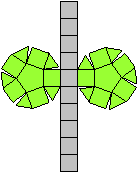
Acht Körper gehen aus
der Fünfeckskuppel hervor.
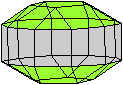
Sieben Körper gehen aus der Fünfecksrotunde
hervor.
Fünf Körper sind Kombinationen von Fünfeckskuppel
und Fünfecksrotunde.
Johnson-Körper
im Internet top
Deutsch
Werner Brefeld
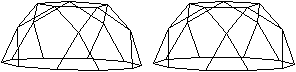
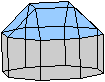
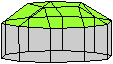
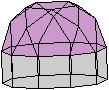
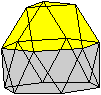
Geodätische
Kuppeln
Wikipedia
Johnson-Körper,
Geodätische
Kuppel, Kuppel,
Norman
Johnson (Mathematiker)
Englisch
Eric W.Weisstein
Johnson
Solid,
Triangular
Cupola, Square
Cupola, Pentagonal
Cupola, Pentagonal
Rotunda,
Geodesic
Dome
Poly
A program
for downloading (Poly is a shareware program for exploring and constructing
polyhedra)
Die meisten Bilder dieser Seite entstanden mit diesem
Programm.
Wikipedia
Johnson
solid,
Triangular
cupola,
Square
cupola,
Pentagonal
cupola,
Pentagonal
rotunda, Geodesic
dome, Dome,
Norman_Johnson
(mathematician)
WolframAlpha
triangular
cupola, square
cupola, pentagonal
cupola, pentagonal
rotunda
Youtube (8zz8)
92
Johnson Solids
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© 2015 Jürgen Köller
top |




 .
.






 ...
...












 ...
... ...
... ...
...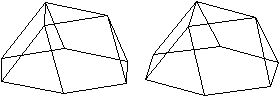
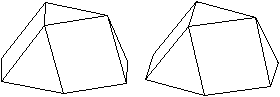
 ...
...
 edron03.gif...
edron03.gif...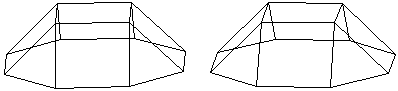






 ...
...



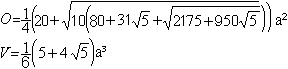
 ...
...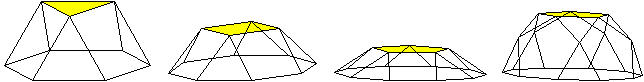
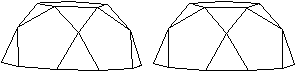
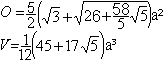
 ...
...
 ...
...
 ...
...

 ...
...
 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...
 ..
.. ...
... ...
... ....
.... ...
...