|
Was ist ein Kaleidoskop?
... ... ... |
Ein Kaleidoskop ("Schönbildseher") ist ein optisches
Spielzeug. Schaut man durch ein kleines Guckloch in eine Röhre und
hält sie gegen das Licht, so sieht man ein prächtiges, symmetrisches
Bild. |
... ... ... |
Es stammt von bunten Glasstückchen und ihren Spiegelbildern,
die drei Spiegel im Inneren erzeugen. Die Glasstückchen sind am anderen
Ende in einer kleinen Kammer frei beweglich eingeschlossen.
Beim Drehen der Röhre verändern sich die Bilder. |
... ... ... |
Im Inneren befinden sich drei längliche Spiegel
in Röhrenlänge, die aneinander stoßen und ein gleichseitiges
Prisma bilden. |
Für diese Webseite kaufte ich ein billiges
Kaleidoskop.
... ... ... |
Das zylindrische Gehäuse ist aus Blech. Links ist
das Guckloch, rechts eine schmale Kammer aus Kunststoff mit den farbigen
Glasstückchen. Das Glas ist durchsichtig und außen durchscheinend.
Schaut man schräg durch die Kammer in das Kaleidoskop,
so erkennt man ein Dreieck, das von den Kanten dreier länglicher Spiegel
gebildet wird. (Hersteller: Simba Toys, Fürth) |
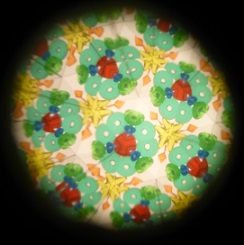
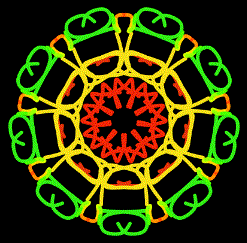
Eine Kamera schaut viermal in das Kaleidoskop
hinein. Nach jedem Schütteln ergeben sich neue Bilder.
Die Fotos geben nicht die Schärfe und die Farbbrillanz
der Bilder wieder, wohl aber den Reichtum an Mustern.
Der englische Physiker David
Brewster ("Brewster-Winkel") hat das Kaleidoskop im 19. Jahrhundert wissenschaftlich
untersucht und populär gemacht.
Das ist das Titelbild des Buches "The Kaleidoscope", dessen
Abdruck man im Internet unter books.google.de findet.
Das Buch beginnt so.

Zustandekommen
des Bildes top
Winkelspiegel 60°
... ... ... |
Stellt man zwei randlose Wandspiegel so vertikal auf,
dass sie sich berühren und einen Winkel von 60° bilden, und befestigt
zwischen ihnen einen Zettel mit der Figur 123, so entstehen fünf Spiegelbilder.
Die Spiegelbilder rechts und links erwartet man. Erstaunlicherweise
werden diese Spiegelbilder wiederum an "imaginären" Spiegeln gespiegelt.
Ein fünftes Bild hinten ist das gemeinsame Spiegelbild der hinteren
Spiegelbilder. |
Strahlenverlauf
beim Winkelspiegel
...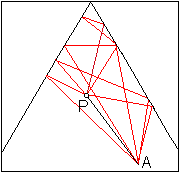 ... ... |
Verfolgt man im Winkelraum eines Winkels von 60°
die Lichtstrahlen, die von Punkt P ausgehen und durch Punkt A verlaufen,
so gibt es sechs Möglichkeiten des Strahlenverlaufs. Da ist einmal
der direkte Weg. Dann werden zwei Strahlen einmal reflektiert, zwei weitere
zweimal und ein Strahl dreimal.
Man kann P als Gegenstand und damit als Quelle der Strahlung
und A als Ort des Empfängers, also des Auges, annehmen.
|
Mehr Klarheit ergibt sich,
wenn man die fünf Fälle der Reflexion getrennt und im Detail
darstellt.
...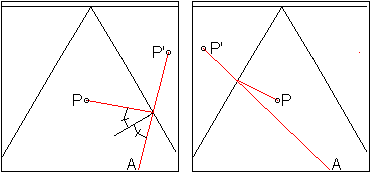 ... ... |
Im einfachsten Fall findet die Reflexion an nur einer
Spiegelfläche statt.
Wie ganz links angedeutet wird so reflektiert, dass Einfalls-
und Reflexionswinkel gleich sind. Einfacher erhält man den Strahlenverlauf,
wenn man den Spiegelpunkt P' von P zu Hilfe nimmt.
Das Auge, das den Strahl registriert, hat den Eindruck,
dass der Strahl nicht von P ausgeht, sondern vom Spiegelpunkt P'. |
...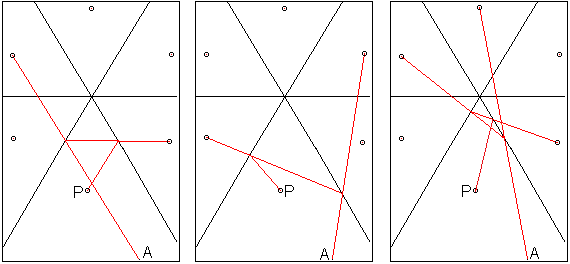 ... ... |
In den übrigen drei Fällen registriert das
Auge Lichtstrahlen, die scheinbar von den drei Spiegelpunkten oberhalb
der Horizontalen ausgehen.
Man sieht also den Punkt P direkt und die fünf Spiegelbilder
scheinbar.
So erklärt sich im Prinzip das Experiment mit den
beiden Wandspiegeln oben. |
Beim Kaleidoskop gibt es
noch einen weiteren Spiegel, der mit den anderen beiden Spiegeln auch einen
Winkel von 60° bildet. So entstehen drei Winkelspiegel. Durch die beiden
neuen Winkelspiegel bilden sich weitere fünf Spiegelbilder, zu diesen
wiederum Spiegelbilder und so setzt sich das (theoretisch) über alle
Grenzen fort.
Kaleidoscope
beim IPad von Apple
Die Bilder der drei Winkelspiegel und damit des Kaleidoskops
lassen sich mit einem Computerprogramm (Photo Booth) des IPads simulieren.
Es gibt weiter Apps für das IPad, die seine Kamera
aufwändiger programmieren. Da ist es z.B. möglich, ein Muster
mit vielen Sechsecken zu erzeugen.
Ein Programm heißt "Kaleidoskop Kamera lite", Entwickler
ist Sebastian Stadtlich in der Version 3.40.
Richtet man die Kamera auf die Figur 123. so ergibt
sich das folgende Bild.
Man sieht in der Mitte das Life-Bild als ein helles Dreieck.
Durch Vielfachspiegelungen ergibt sich ein Bild wie bei einem Kaleidoskop.
Weiteres
Bild
Man würde nie glauben, dass ein Kunststoffbecher auf
dem Gartentisch Vorlage für dieses Bild ist.
Aufenthalt
im Kaleidoskop top
... ... ... |
Im Exploratorium, dem naturwissenschaftlichen Mitmach-Museum
in San Francisco, fand ich eine Station, bei der man in ein Kaleidoskop
einsteigen konnte. Die Station bestand aus einem Gestell mit drei Spiegeln,
die zusammen ein Dreiecksprisma mit einem gleichseitigen Grunddreieck bildeten.
Man konnte sich in das Prisma von unten begeben, indem man sich bückte
und wieder aufrichtete.
Das eigene Spiegelbild war vielfach in mehreren Richtungen
auszumachen.
Ich möchte empfehlen, es im Physikunterricht aus
drei Wandspiegeln nachzubauen.
Man bildet aus drei Bänken ein U, stellt auf sie
die Spiegel und fixiert sie. |
Kaleidoskop
mit vier Spiegeln top
...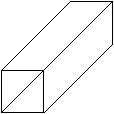 ... ... |
Kaleidoskope mit drei Spiegeln sind Standard. Man baut
sie auch aus vier Spiegeln. Sie bilden dann ein Quadrat.
Sie erzeugen Bilder mit quadratischer Struktur, die sich
bei Bewegung auf und ab bzw. hin und her bewegen. |
...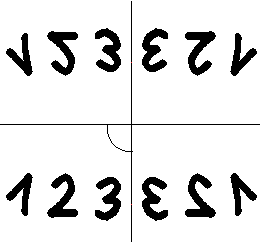 ... ... |
Grundlage ist wieder ein Winkelspiegel, dieses Mal mit
einem Winkel von 90°.
Es entstehen wie erwartet oben und rechts zwei Spiegelbilder.
Die Zahlen 123 erscheinen in Spiegelschrift. Das dritte Bild oben rechts
zeigt die Ausgangsfigur um 180° gedreht.
Schaltet man einen zweiten 90°-Winkelspiegel davor,
so entsteht ein Muster aus vielen Spiegelbildern. |
Das Muster sieht so aus.
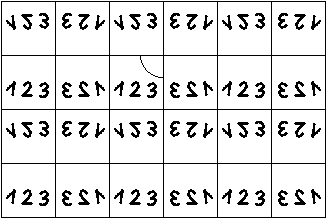
Man kann auch Kaleidoskope
mit Winkeln 360°/n (n=5, 6, ...) mit regelmäßigen Vielecken
als Querschnitt bauen. Ob das sinnvoll ist, wird auf der Webseite von ZUM-Wiki
untersucht (URL unten).
Ein
weiteres Kaleidoskop mit drei Spiegeln top
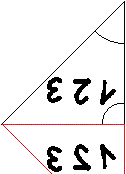
Ein Winkelspiegel mit einem Winkel von 45° erzeugt sieben
Spiegelbilder von 123, die zusammen eine Quadrat bilden. Man könnte
vor diesem Winkelspiegel einen weiteren Spiegel anbringen, so dass ein
45°-90°-45°-Dreieck entsteht.
Das so entstandene Kaleidoskop ist eine Kombination von
drei Winkelspiegeln mit 45°, 90° und 45°.
Das folgende Bild entsteht.
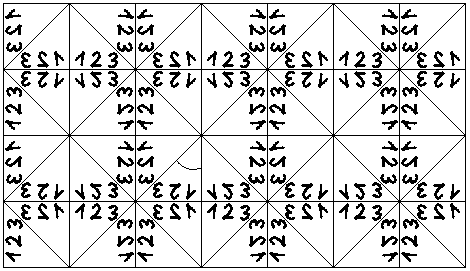
Es gibt nur noch ein dreieckiges
Kaleidoskop mit spitzen bzw. einem rechten Winkeln, nämlich das mit
den Winkeln 30°-60°-90°.
Die Winkel a, b und c der Dreiecke müssen ein Teiler
von 360° sein, und es muss a+b+c = 180° gelten.
Unter diesen Bedingungen gibt es nur die Lösungen
60°-60°-60°, 45°-45°-90° und 30°-60°-90°.
Das bestätigt ein Computerprogramm.
Vielstrahlige Figuren
top
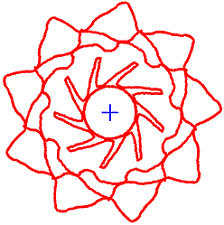
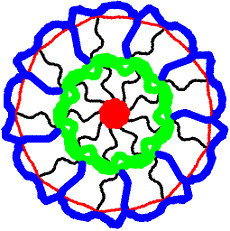
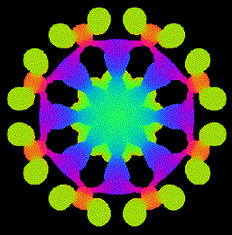
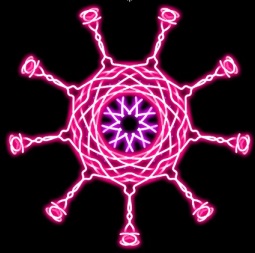
Es gibt im Internet zahlreiche Applets mit dem Namen
Kaleidoskop. Sie simulieren jedoch nur den Winkelspiegel. Doch auch diese
Bilder sind ansehnlich. Eine neunstrahlige Figur z.B. entsteht so, dass
man nur die Linien in einem Kreisausschnitt mit einem Winkel von 360°/9
=40° zeichnet. Das Programm zeichnet sie gleichzeitig in die übrigen
acht Kreisausschnitte ein. - Meist kann man an Stelle von n=9 die
ersten natürlichen Zahlen einstellen.
Ich weise auf vier Programme hin.
1
Symmetry Artist von MathsIsFun.com (URL unten)
|
2
Kaleidoscope Painter von F. Permadi (URL unten)
|
3
Online Kaleidoskop von Marcel Liebing (URL unten)
4
Das vierte Programm ist ein App für das IPad [Kaleido
free (Kaleidoscope Drawing Pad), Entwickler Guoyan Han Version 1.4.9 ].
An anderen Stellen meiner Homepage findet
man die Webseiten Dreistrahlige Figuren,
Vierstrahlige
Figuren und Fünfstrahlige Figuren,
die zu diesem Kapitel passen..
... ... ... |
Aus dem Wort Kaleidoskop entstand Kaleidozyklus.
Das ist eine Bastelei aus Papier, nämlich ein Ring
aus Tetraedern, den man ohne Ende in sich drehen kann.
Mehr auf meiner Seite Kaleidozyklen |
Bau eines Kaleidoskops
top
Ich erinnere mich, dass in den siebziger Jahren Kaleidoskope
vom Spielzeugmarkt so ziemlich verschwunden waren, so dass ich ein Exemplar
für die Physiksammlung baute. Heute haben die meisten Spielzeugläden
Kaleidoskope (auch als billige Massenware, s.o.) im Sortiment. Im Internet
findet man ebenfalls etliche Bezugsquellen.
Trotzdem ist es eine Herausforderung, ein Kaleidoskop
selbst zu bauen. Und da gibt es zahlreiche Links zu Seiten mit Bauanleitungen.
Man findet sie mit Hilfe von Google und den Suchbegriffen "Kaleidoskop
basteln", "Kaleidoskop bauen", "making of a kaleidoscope" oder "how to
make a kaleidoscope".
Wenn ich eine Anleitung empfehlen sollte, würde
ich die von GEO.de (URL unten) nennen.
Die Zeiten haben sich geändert. Spiegelfolie scheint
eine Alternative zum Glasspiegel zu sein.
Der Glasspiegel hat den Nachteil, dass das Licht auch
an der Oberfläche durch Totalreflexion reflektiert wird.
Auch wenn Aluminiumfolie manchmal genannt wird, so scheidet
sie aus, da sie zwar Licht reflektiert, aber keine Spiegelbilder liefert.
Kaleidoskop
im Internet top
Deutsch
Bild der Wissenschaft
Bunte
Muster in Rekordgröße
Jürgen Richter-Gebert (Technische Universität
München)
Blicke
in die Unendlichkeit
M. & U. Karl
KARLEIDOSKOP
Marcel Liebing
Online
Kaleidoskop
Martin Gagern
Winkelspiegel
Spiegel online ( 20.11.2014)
Kaleidoskop-Technik: Das
Schöne im Biest
Wikipedia
Kaleidoskop,
Photo
Booth, Exploratorium,
Denkmal
für die Kinder in Yad Vashem
ZUM-Wiki
Kaleidoskop
Englisch
AngelGilding.com
Angled
Mirrors & Multiple Reflections
Brewster Kaleidoscope Society
The
Kaleidoscope On-Line Book
David Brewster (http://books.google.de)
The
Kaleidoscope
F. Permadi
Kaleidoscope
Painter
MathsIsFun.com
Symmetry
Artist
Wayne Schmidt
KALEIDOSCOPE
MIRROR DESIGNS
Wikipedia
Kaleidoscope,
Photo
Booth, Exploratorium
Youtube
The
Splendor of Color Kaleidoscope, TEDxSummit
intro: The power of x
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
http://www.mathematische-basteleien.de/
© 11/2014 Jürgen
Köller
top |



 ...
... ...
... ...
... ...
...





 ...
... ...
... ...
... ...
...



 ...
... ...
...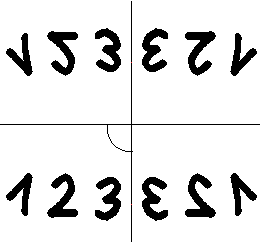 ...
...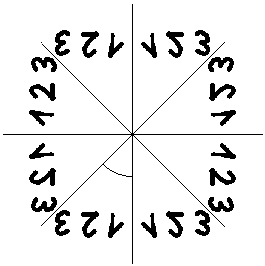






 ...
...