|
What is a Kaleidocycle?
... ...
K1 ...
K1
|
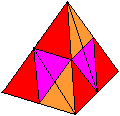
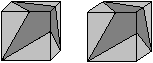
The simplest kaleidocycle is a ring of an even number
of tetrahedra. (Tetrahedra are pyramids with equal edges and equilateral
triangles as sides.)
The tetrahedra are connected on perpendicular edges.
What makes it special is that you can continually twist
it inwards or outwards while it shows different sides of each tetrahedron. |
There is an infinite number of kaleidocycles. The tetrahedra
becomes a pyramid then.
On this page I introduce and describe special kaleidocycles.
I number them with K1 to
K15.
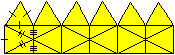
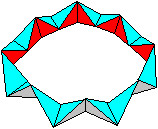
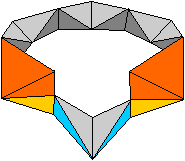
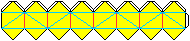
The Ring
of Eight Tetrahedra
top

K2
The
smallest amount is eight tetrahedra.
... ... ... |
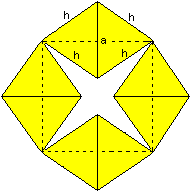
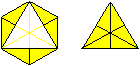
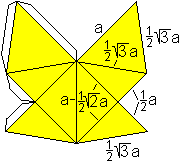
The drawing on the left shows a position, where the joint
edges are horizontal or vertical.
In the drawing on the right you see a cross-section of
this model. a is the edge of a tetrahedron, h=sqrt(3)/2*a is the altitude
of an equilateral triangle.
The square with the broken line is the foundation of
the ring. |
... ... ... |
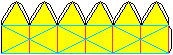
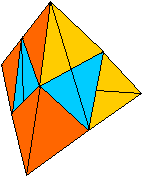
Making
of the Ring
You can produce the ring with paper.
You can make the eight tetrahedra
separately and connect them with adhesive tape. This is simple, but long
work.
It is more challenging to design
a net of the ring, but folding it is a bit more difficult.
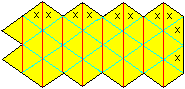
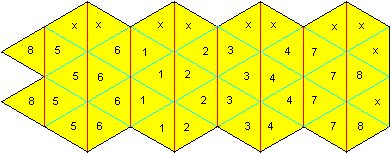 1) Draw the net with equilateral triangles with compasses
and a ruler. The numbers 1 to 8 are only for explaining. The x indicates
the surfaces to be glued together.
1) Draw the net with equilateral triangles with compasses
and a ruler. The numbers 1 to 8 are only for explaining. The x indicates
the surfaces to be glued together.
The length of a triangle is e.g. 2.5 cm; then the drawing
fits an A4 page.
(2) Cut out the net.
(3) Go over the lines with a ballpen or the blunt edge
of scissors, so that you can fold the paper at the lines more easily. Fold
the paper several times.
(4) First form the tetrahedra 1111 and 2222 at the same
time. Glue the triangles xx (top) on the triangles 12 (down).
(5) Repeat the process with the pairs 3333/4444, 5555/6666
and 7777/8x8x in this order.
(6) Close the ring by gluing the triangles 88 on xx last.
If you want to make rings with 10,12,14, ... tetrahedra,
put in more strips.
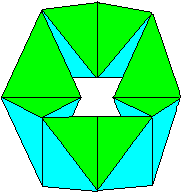
Closed
Ring of Six Pyramids top

K3
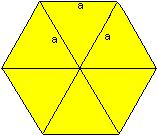
If you try to assemble six tetrahedra to a ring, you see
that they don't form a ring (picture on the left). You must stretch the
tetrahedra, so that you achieve a ring. In the borderline case you have
a hexagon as a cross-section (picture in the middle). On the right you
can see the ring.
There is a right angled triangle with the sides b, a
and a/2. The Pythagorean theorem gives b²=a²+(a/2)²
or b=sqrt(5)/2*a.
You have 4-sided pyramids
instead of tetrahedra.
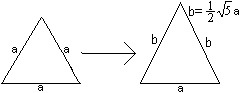 ... ...
|
The triangles of the tetrahedra are no longer equilateral
but isosceles.
The ratio of one side to the other one is b : a = 1.12
: 1.
|
Template:
M.C.Escher
Kaleidocycles
top
.. ... ... |
In the book (1) below, the ring with stretched tetrahedra
is called kaleidocycle. This name is generally accepted because of the
world-wide spread of this book.
The book has 14 models and instructions, among them several
rings.
The models are decorated with parts of the paintings
of the Dutchman M.C.Escher. So they become nice and unique.
A closed kaleidocycle is fascinating, because there is
a lot of movement during rotation. The middle is opened and closed
regularly. |
Closed
Ring of Eight Pyramids top

K4
.. .... .... |
If the ring of eight tetrahedra from above shouldn't
have a hole, you must change the shape.
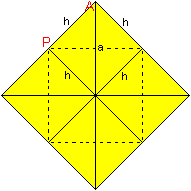
That leads to a square as a cross-section. You must imagine
that there are edges perpendicular to the drawing-board going through the
middles of the sides. P is one centre point. |
 ...... ...... |
...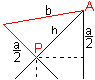 ...E ...E |
If you turn the vertical edge a in P in the drawing board,
you get a right angled triangle.
You can calculate the length of the edge b of the pyramid:
b²=(a/2)²+h².
You get b=[sqrt(3)/2]a with h=sqrt(2)/2*a. |
You have 4-sided pyramids
instead of tetrahedra. The triangles are no longer equilateral but isosceles.
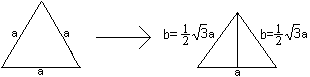
|
The ratio of one side to the other one is b : a = 0,87
: 1. |
Template:
Origin: Randolf Rehfeld
The Invertible Cube
top
...
K5
How to make it
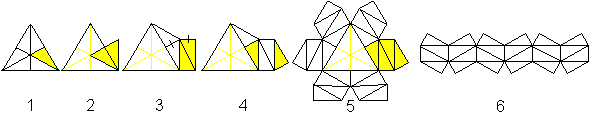 (1) Draw an equilateral triangle and its medians (a=5cm for
example).
(1) Draw an equilateral triangle and its medians (a=5cm for
example).
(2) Reflect a triangle on a side.
(3) Erect a rectangle on the hypotenuse of the reflected
triangle. The marked lines are equal.
(4) Put the triangle on the rectangle.
(5) Repeat this process five times. Fold a pyramid of
the four yellow right angled triangles.
(6) Form a row and add strips on the triangles to fix
the pyramids and to close the ring later.
Result: You get a kaleidocycle of six pyramids with a
triangular hole.
Template

Description
... ... ... |
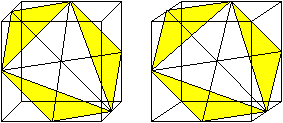
There are four positions remarkable while twisting inwards:
(1) Six triangles of the pyramids lie in the plain (picture
1). They form a hollow hexagon in the front.
(2) You twist further. There is the same hexagon on the
reverse side.
(3) Then the six triangles form an equilateral triangle
on the reverse side.
(4) This triangle turns to the front side (picture 2). |
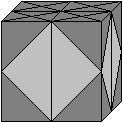
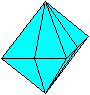
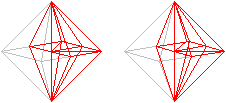
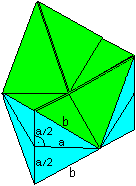
This kaleidocycle is known as the invertible cube or Schatz
cube.
To explain the name "invertible
cube", you may think to look at the well known hexagon inside a cube. You
can see the triangles inside and outside the hexagon, but I found no relation
to the whole pyramids.
If you can use the 3D-view, you recognize the six basic
sides of the pyramids.
This explains the name "invertible cube":
You can turn the ring so that the right angles of the
triangles are used to form corners of the cube:
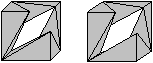
You recognize the six pyramids of the ring. The cube is
not solid. The pyramids only fill a third of the cube. You can prove it:
Calculation
...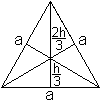 ... ... |
A pyramid is formed by four triangles inside an equilateral
triangle with the side a. A triangle has the sides a/2, h/3, and 2h/3.
The height is h=[sqrt(3)/2]a.
The length of the side of the cube is a/2 and thus the
volume is V'=a³/8.
The pyramids altogether have the volume 6*(1/3)*area
of the triangle*height. |
This is here V=6(1/3)[(1/2)(a/2)(h/3)][h/3]=(1/24)a³.
Therefore is V=V'/3.
If you want to complete the
cube as a solid cube, you need two equal "bolts" to put into the hollow
cube.
The Ring Half
Octahedrontop

K6
You can develop the invertible cube
to a ring with an open square instead of an equilateral triangle
using special positions.
How
to make it
 (1) Draw a square with diagonals and its medians ( a=5cm
for example).
(1) Draw a square with diagonals and its medians ( a=5cm
for example).
(2) Reflect a triangle on a side.
(3) Erect a rectangle on the hypotenuse of the reflected
triangle. The marked lines are equal.
(4) Put the triangle on the rectangle.
(5) Repeat this process seven times. Fold a pyramid of
the four right triangles.
(6) Form a row and add strips on the triangles to fix
the pyramids and to close the ring later.
Template
This ring is called half
octahedron here, because you can fold this ring to a (red) half octahedron.
Origin: Randolf Rehfeld (URL below) - There is a template.
You get more kaleidocycles,
if you start with higher regular polygons.
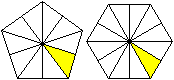
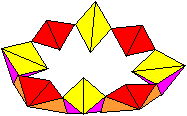
Double Crown top
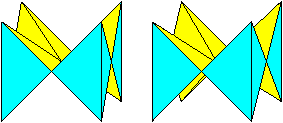
K15
... ... ... |
... ... ... |
The kaleidocycle, which can be folded to a half octahedron,
has a square window.
If you fold it further, you get a "crown" with four points.
The base of this crown is a square.
Reflect it on the square as mirror. |
...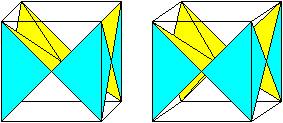 ... ... |
This leads to a new kaleidocycle, the "double crown".
I didn't find a better name. You can recognize in this position that there
is a relationship to a surrounding cube. Two triangular pyramids form an
edge of the cube.
A calculation shows that the kaleidocycle is filling
a third of the cube. |
In this partition the cube
is called Schneider-Würfel on Margarita Ehrlich's and Ellen Pawlowski's
German web sites (URL below).
transparent cube
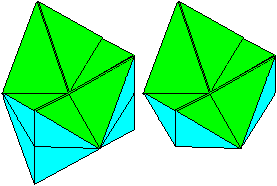
|
one triangular pyramid
|
4x
|
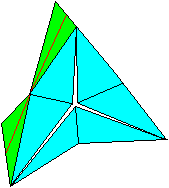
Four "butterflies" can be used as templates (a=5cm).
Each figure forms an edge of the corresponding cube.
The strips for glueing are missing on the right. |
... ... ... |
You can turn this kaleidocycle in that way that a crown
with square base arises again.
The four points are lower.
You can again reflect this crown on a square and - voilá
- you have a new kaleidocycle... |
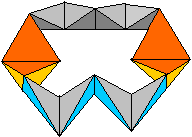
The
Half Closed Ring of Six Pyramids top

K7
How to make this ring
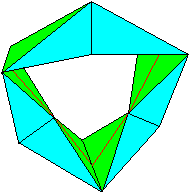
... ... ... |
The closed ring of six pyramids
from above has a symmetry plane. You can lay an intersection in it. A kaleidocycle
develops which is erected over a regular hexagon.
It is special that the common edges
are no longer the same. |
If you twist the ring, you get two remarkable positions of
the ring.
The opening is an equilateral triangle (red).
The shape is a non-regular hexagon with equal sides.
|
The shape is an equilateral triangle (red).
The ring is nearly closed.
|
There is a symmetry plane in both cases (marked red).
Six
squares and equilateral triangles on top form the net.
The marked lines are the same. Those
with one small stroke have the length a, with two strokes b=sqrt(5)/2*a
and with three strokes a/2.
There is a similarity with
the invertible cube described above.
In both cases there are positions with a triangle as
silhouette. But it isn't closed as Schatz cube is. The edge a/2 is slightly
shorter than
sqrt(3)/3*a=0,56a at the Schatz cube.
This ring ought to be a hint to
look for new kaleidocycles and to work on them.
You could already read above that there is an endless
number of kaleidocycles.
A "normal" kaleidocycle is always formed if there are
two opposite edges in pairs and a common perpendicular orthogonal.
The Shinsei Miracle
top
There is a golden/silver cube which was developped by
Naoki Yoshimoto in the 1970s. You can take it apart and - a surprise! -
you get two kaleidocycles of 12 pyramids.
You can read more on my German page The
Shinsei Miracle.
Cube One top
Cube One is a new cube puzzle invented by the graphic
designer and artist Dieter A.W. Junker from Kassel / Germany.
The challenge is to form a cube of 2x2 Kaleidocycles.
Each kaleidocycle is a puzzle
itsself.
One is leading to a tetrahedron, the other to an octahedron.
You can find more on my page Cube
One.
Tetra One top
Tetra One is another puzzle developped
by Dieter A.W. Junker.
The challenge is to form a tetrahedron with two Kaleidocycles.
Both kaleidocycles only differ in the order of the pyramids.
You can find more on my page Tetra
One.
Templates top
You find descriptions on this page how to draw nets in
order to build kaleidocycles.
But it is easier to use the templates which are available
on the internet. I add the names Ki
in my list of links and books, if you can find a template.
Have fun in building kaleidocycles
and in looking for new shapes.
Kaleidocycles
on the Internet top
German
Franz Zahaurek
Der umstülpbare Würfel
nach Paul Schatz
Randolf Rehfeld (Wundersames Sammelsurium)
Kaleidozyklen...K2,
K3, K4, K5, K6
English
Akira Nishihara
Ring
of tetrahedrons
Arvind Gupta
PAPER
FLEXAGON ENGLISH 20MB (Video at Youtube)
David Singmaster
Cubic
Circular (magazine Issue 5 & 6 - #11 - #13) (Autumn &
Winter 1982)
Enchanted Learning online
Make
A 3-D Hexaflexagon ... K2
FoldPlay
MAKE
YOUR VERY OWN PHOTO KALEIDOCYCLE
G. Korthals Altes
Paper Models
of Polyhedra
Kaleidocycles: Hexagonal Kaleidocycle K3,
Octagonal Kaleidocycle K2, Decagonal Kaleidocycle
K1
Herbert Kociemba
Kaleidocycles
with 6 Disphenoids
instructables craft
Kaleidocycle
Jaap Scherphuis
Pyrix
(Chain of 4 octahedrons + 11 tetrahedrons = 1 large tetrahedron)
Maurice STARCK
a
ride through the polyhedra world
Kristina
Burczyk's Kaleidocycles
Coloured Kaleidocycles with opened triangulars
Paul Jackson
Origami
Hexaflexagon (Video bei Youtube)
Youtube
How
to Make a Kaleidocycle
Wikipedia
Kaleidocycle
French
Peuplier (Le Forum en Papier)
Kaleïdocycle
didactique, le moteur 4 temps K4
Cube
magique, Shinsei Mystery (ou Miracle) K8
References top
(1) Doris Schattschneider und Wallace Walker, M.C.Escher
Kaleidozyklen, Köln 1992 K3 K4

|
The drilled kaleidocycle K9 |
(2) Gerald Jenkins and Anne Wild, Make Shapes 1, Diss
(Norfolk), Tarqin Publications, 1998 K1
Gail from Oregon Coast, thank you for supporting
me in translating this website.
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2005 Jürgen Köller
top |







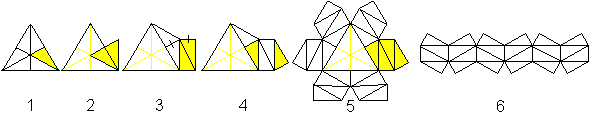




 ...
...
 ...
... ...
...
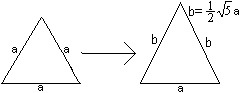 ...
... ...
... ......
...... ...E
...E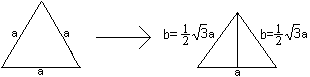
 ...
...

 ...
...

 ...
... ...
...


 ...
... ...
...