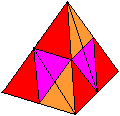
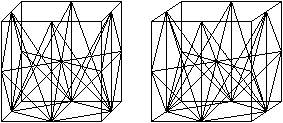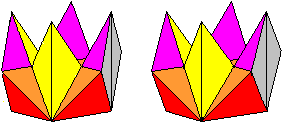|
What is Cube One ?
Cube One is a new cube puzzle invented by the
graphic designer and artist Dieter A.W. Junker from Kassel / Germany.
The object is to build a cube with four chains of pyramids
(kaleidocycles).
Drawings:
|
>
|
|
Every kaleidocycle is a puzzle itself. The first chain leads
to a tetrahedron, the second one to an octahedron.
|
>
|
|
|
>
|
|
I use the same colours
for my drawings as in the puzzle.
Investigation
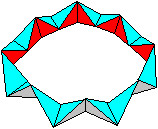
of the Octahedron Chain top
Description
|
......
|
16 congruent pyramids form the octahedron chain.
Two pyramids are symmetric to each other. |
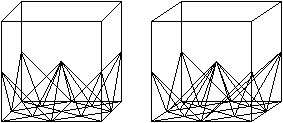
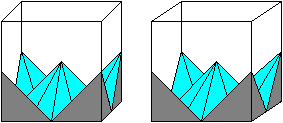
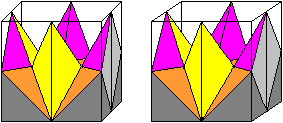
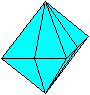
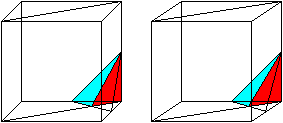
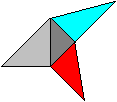
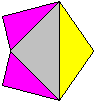
Formation
of the pyramid red/blue
There is a pyramid at the corner of the cube, if you
connect the centre points of three edges. If you lay a section through
the diagonals of the cube, the pyramid at the corner is halved. This solid
is the pyramid of the octahedron chain.
You can see the position in the following 3D-picture.
Measurements of the pyramid
|
Let "a" be the length of an edge of the cube.
The grey basic triangle has the sides a/2 and sqrt(2)/4*a
twice.
The light grey triangle has the sides sqrt(2)/2*a
and a/2 twice.
The blue triangle has the sides sqrt(2)/2*a, sqrt(2)/4*a,
and sqrt(2)/4*a.
The red triangle has the sides a/2, sqrt(2)/4*a, and
sqrt(2)/4*a. |
Volume
The pyramid has the grey triangle as basic triangle and
the height a/2.
The volume V1' is (1/3)*[(1/2)(a/2)*(a/2)/2]*(a/2)=a³/96.
The octahedron chain has the volume V1= 16V1'
=16a³/96=a³/6.
Investigation
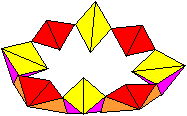
of the Tetrahedron Chain top
Description
| ...... |
16 congruent pyramids form the tetrahedron chain
There are two kinds of pyramids, the pyramid violet/yellow
and the pyramid red/orange.
Two pyramids are symmetrical to each other. |
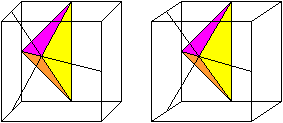
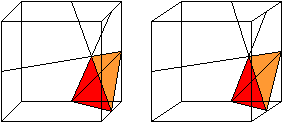
Formation
of the first pyramid (violet/yellow)
You get a pyramid if you connect certain centres of the
edges.
You can see this in a 3d-picture.
Measurements
of the pyramid
... ...
|
Let "a" be the length of an edge of the cube.
The grey triangle has the sides "a" and sqrt(2)/2*a twice.
The yellow triangle has the sides "a" and sqrt(6)/4*a
twice.
The violet triangles are congruent and have the sides
sqrt(2)/2*a, sqrt(2)/4*a, and sqrt(6)/4*a. |
Volume
The pyramid has the yellow triangle as basic triangle
and the height sqrt(6)/4*a.
The volume V21' is (1/3)*[(a/2)*(sqrt(2)/4*a]*(sqrt(2)/4)*a)=a³/48.
Formation
of the second pyramid (red/orange)
You get a pyramid if you connect certain centres of the
edges.
You can see this in a 3d-picture.
Measurements
of the pyramid
... ...
|
Let "a" be the length of an edge of the cube.
The triangle in the centre is equilateral and has the
sides sqrt(2)/2*a.
The red triangle below has the sides sqrt(2)/2*a and
sqrt(6)/4*a twice.
The violet triangles are congruent and have the sides
sqrt(2)/2*a, sqrt(2)/4*a, and sqrt(6)/4*a. |
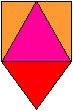
Volume
The pyramid has the red triangle as basic triangle and
the height sqrt(2)/4*a.
The volume V22' is (1/3)*[(a/2)*(sqrt(2)/4*a]*(sqrt(2)/4)*a)=a³/48.
Volume
of the tetrahedron chain
Eight pyramids violet/yellow and eight pyramids red/orange
form the tetrahedron chain.
With that the volume is V2=8*V21'
+
8V22' = 8a³/48+8a³/48=a³/3.
Division
of the cube
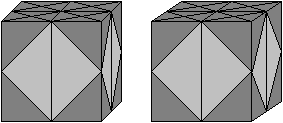
Solution of Cube
One top
First step
| ...... |
You put the octahedron chain on a plane as shown on the
left and push together the pair of pyramids so that the red faces touch
each other. |
You get an opened octahedron as shown in the next 3d picture.
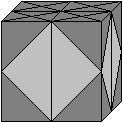
transparent
You put this body in the
transparent plastic cube, which belongs to this puzzle.
Second step
| ...... |
You put the tetrahedron chain on the desk as shown on
the left.
You must form the "crown". In the beginning it is slightly
difficult.
Look at the yellow triangles. The four triangles at the
top and below become the outer edges of the crown. The yellow triangles
on the right and left approach inside.
You must turn the chain. This is only possible with light
power. |
transparent
non-transparent and coloured
Put the crown into the cube on the octahedron
chain.
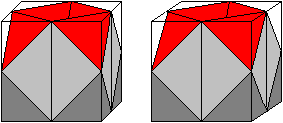
Third
step
Form a second crown from the tetrahedron chain and put
it on the first one upside down.
Fourth step
Close the cube with a second opened octahedron.
Second
solution
There is a second solution as the inventor tells. This
solved cube has this appearance.
You find more about kaleidocycles on my homepage: Kaleidocycles
(German/English)
The Shinsei Miracle (German
only)
Cube One on
the Internet top
Dieter A.W. Junker
Flyping
Games (German/English)
English / German
During the first ten years I translated my German-language
web pages as best I could.
Back then, English was the language of the Internet even
more so than it is today.
If anything is unclear, please visit my German-language
website and use a translation program.
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2006 Jürgen Köller
top |