Tetraederzahlen
Inhalt dieser Seite
Was ist eine Tetraederzahl?
Entstehung
Formel		 Besondere Tetraederzahlen
Lage im Pascalschen Dreieck
Tetraederzahlen im Internet.
Zur Hauptseite    "Mathematische Basteleien"

Was ist eine Tetraederzahl?
Eine Tetraederzahl ist eine Zahl aus der Folge 1, 4, 10, 20, ...
Das Bildungsgesetz ist tn=n(n+1)(n+2)/6.

Das sind die ersten 100 Tetraederzahlen:

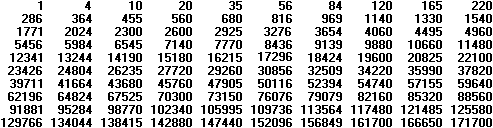
Die Tetraederzahlen sind überwiegend gerade Zahlen. Jede fünfte Zahl ist ungerade.
Die Tetraederzahlen enden mit den Ziffern 0, 1, 4, 5, 6 oder 9.


Die Tetraederzahl heißt auch tetraedische Zahl.

Entstehung   top
Die Tetraederzahlen entstehen, wenn man zu der Folge der Dreieckszahlen 1,3,6,10,15,21,28,... die Reihe bildet.

Die Folge der Dreieckzahlen ist, das sei noch einmal erwähnt, die Reihe der natürlichen Zahlen. 
1, 1+2=3, 1+2+3=6, 1+2+3+4=10, 1+2+3+4+5=15, 1+2+3+4+5+6=21, 1+2+3+4+5+6+7=28,...

Nach der gleichen Regel entstehen aus den Dreieckzahlen die Tetraederzahlen.
1, 1+3=4, 1+3+6=10, 1+3+6+10=20, 1+3+6+10+15=35, 1+3+6+10+15+21=56, ...

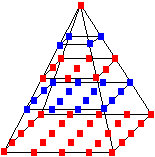
Die folgende Zeichnung erklärt den Namen Tetraederzahl. Die Zahl 56 ist exemplarisch.
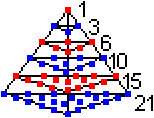Man stelle sich 56 Kugeln vor, 56 =1+3+6+10+15+21.

Dann lassen sich die Kugeln in 6 Schichten in Dreiecksform stapeln, so dass ein Tetraeder entsteht.

Formel    top
Die Tetraederzahl hat die Darstellung tn=n*(n+1)*(n+2)/6, wobei n eine natürliche Zahl ist. 
Erster Beweis

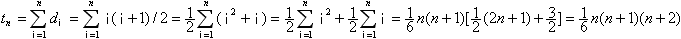
Dabei werden die Formeln 1+2+3+4+...n=n(n+1)/2 und 1²+2²+3²+4²...n²=n(n+1)(2n+1)/6 vorausgesetzt.

Zweiter Beweis
Die Formel soll nach der Methode der vollständigen Induktion bewiesen werden. 
Voraussetzung: Die allgemeine Darstellung einer Dreieckszahl ist dn= n(n + 1)/2.
Behauptung: Die Tetraederzahl hat die Darstellung tn=n*(n+1)*(n+2)/6.
Die Formel gilt für n=1, denn t1=1*2*3/6=1.
Angenommen, die Formel  gilt für n.: tn=n*(n+1)*(n+2)/6. Dann muss tn+1= (n+1)*(n+2)*(n+3)/6 daraus folgen.
Nachweis:  tn+1=  tn+(n+1)*(n+2)/2=n*(n+1)*(n+2)/6+(n+1)*(n+2)/2=(n+1)*(n+2)[n/6+1/2]=(n+1)*(n+2)*(n+3)/6 wzbw.

Besondere Tetraederzahlen top
In diesem Kapitel wird auf figurierte Zahlen eingegangen, also auf  Zahlen, die durch Figuren oder Körper veranschaulicht werden können. Dabei geht es um die Frage, welche figurierte Zahlen gleichzeitig Tetraederzahlen sind. 
Polygonzahlen oder Vieleckszahlen
Polygonzahlen sind Zahlen, die man durch Vielecke veranschaulichen kann. 

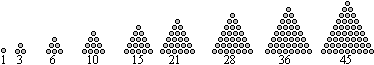
Dreieckszahlen

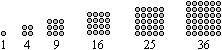
Quadratzahlen

Übersicht über die ersten Polygonzahlen
Name
Dreieckzahlen
Quadratzahlen
Fünfeckzahlen
Sechseckzahlen
Siebeneckzahlen
Achteckzahlen
...		 n-tes Glied
n*(n+1)/2
n²
n*(3n-1)/2
n*(4n-2)/2
n*(5n-3)/2
n*(6n-4)/2
...		 Die ersten Glieder
1 3 6 10 15 21 28... 
1 4 9 16 25 36 49... 
1 5 12 22 35 51 70... 
1 6 15 28 45 66 91... 
1 7 18 34 55 81 112... 
1 8 21 40 65 96 133...
...		 Die ersten Tetraederzahlen
t(1)=1 t(3)=10 t(8)=120 t(20)=1540 t(34)=7140
t(1)=1 t(2)=4 t(48)=19600
t(1)=1 t(5)=35
t(1)=1 t(8)=120 t(20)=1540 t(34)=7140
t(1)=1 t(11)=286
t(1)=1 t(14)=560
...
In der letzten Spalte stehen nur die Tetraederzahlen unter den ersten 100 Zahlen.
Pyramidenzahlen
Das Tetraeder ist eine dreiseitige Pyramide. 
Deshalb heißen die Tetraederzahlen auch Pyramidenzahlen, genauer (aber unschön) die dreiseitigen Pyramidenzahlen.
Als Pyramidenzahlen bezeichnet man allerdings die Zahlen, die aus Quadratzahlen hervorgehen. 
Genauer heißen sie quadratische Pyramidenzahlen. 
...... So wie die Reihe der Dreieckszahlen die Tetraederzahlen sind, so führen die Quadratzahlen zu den Pyramidenzahlen:
1, 1+4=5, 1+4+9=14, 1+4+9+16=30, 1+4+9+16+25=55, ...

Allgemein gilt pn=1²+2²+3²+4²+...+n²=n*(n+1)*(2n+1)/6.
Bis auf die Zahl 1 gibt es keine Tetraederzahl, die gleichzeitig Pyramidenzahl ist. 
Es gilt ein interessanter Satz:
Die Summer zweier aufeinanderfolgender Tetraederzahlen ist eine Pyramidenzahl. 
Beweis:
tn+ tn+1=n*(n+1)*(n+2)/6 + (n+1)*(n+2)*(n+3)/6 = [(n+1)(n+2)/6]*(n+n+3)=(n+1)(n+2)(2n+3)/6=pn , wzbw.
Kuriositäten
>Die folgenden Tetraederzahlen sind Palindrome. t17=969,  t21=1771, t336=6378736
>Sowohl 5456 als auch die rückwärts gelesene Zahl 6545 sind Tetraederzahlen ( t31 und t33 ).
>Es gilt 35=1+4+10+20 oder t5=t1+t2+t3+t4.
>Es gilt 680=560+120 oder t15=t14+t8. 
>Die folgenden Tetraederzahlen lassen sich als Produkt aufeinanderfolgender natürlicher Zahlen schreiben. 
   t4=20=4*5,   t6=56=7*8   und   t34=7140=84*85. 
>Die Tetraederzahl 120 lässt sich als Produkt dreier aufeinanderfolgender natürlicher Zahlen schreiben: t8=120=4*5*6 .

Lage im Pascalschen Dreieck top
......
 Wie so oft in der Zahlentheorie bietet auch hier das Pascaldreieck einen Beitrag.

Die rot gekennzeichneten Zahlen sind Tetraederzahlen. 
Damit lassen sich die Tetraederzahlen 1, 4, 10, 20, ... auch als Binomialkoeffizienten darstellen.

Tetraederzahlen im Internet    top

Deutsch

Wikipedia
Tetraederzahl, Pyramidenzahl

Englisch

Eric W. Weisstein (MathWorld)
Tetrahedral Number, Truncated Tetrahedral Number 

Patrick De Geest 
Palindromic Tetrahedrals

Wikipedia
Tetrahedral number,  Triangular number,  Pyramidal number, Pascal's Triangle

 Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
https://www.mathematische-basteleien.de/

©  2006 Jürgen Köller

top
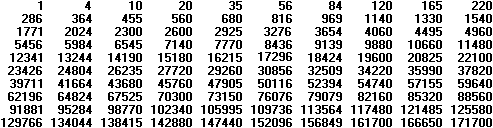
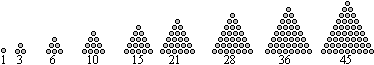
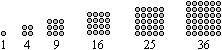