12
Kubikzahlen
Inhalt dieser Seite
Was ist eine Kubikzahl?
Kubikwurzel
Dritte Wurzeln aus negativen Zahlen?
Folgen und Reihen
WARINGsches Problem		 Besondere Kubikzahlen
Zahlenspielereien
Kubikzahlen im Internet
Referenzen
. 
Zur Hauptseite    "Mathematische Basteleien"

Was ist eine Kubikzahl?
Eine Kubikzahl (oder ein Kubus) ist eine Zahl, die sich als Produkt dreier gleicher Faktoren aus natürlichen Zahlen schreiben lässt. 
Formel: k=a*a*a=a³ (k und a stehen für natürliche Zahlen)

Umgekehrt entsteht eine Kubikzahl, wenn man eine natürliche Zahl dreimal mit sich selbst multipliziert. 
Der gleiche Faktor heißt Grundzahl.
Formel: a*a*a=a³=k  (a und k stehen für natürliche Zahlen)
Danach sind eine negative ganze Zahl wie (-2)³= -8 oder eine Bruchzahl wie (2/3)³=8/27 hier ausgeschlossen. 
Wenn es zweckmäßig ist, kann man auch die Zahl 0 als Kubikzahl zulassen.
Das sind die ersten 100 Kubikzahlen.

Der Name erklärt sich aus der Veranschaulichung der Kubikzahlen durch Würfel oder Kuben.
Ist die Kantenlänge eines Würfels a, so ist das Volumen a³.

...1...

8

27
Die Bildpaare ermöglichen eine 3-D-Ansicht.

Kubikwurzel   top
Es ist einfach, eine Kubikzahl zu bestimmen. Es ist schwieriger, zu einer Kubikzahl die Grundzahl zu finden. 
Diesen Vorgang nennt man Wurzel ziehen oder radizieren, die Grundzahl heißt Kubikwurzel. 
 
Die Kubikwurzel aus einer natürlichen Zahl a schreibt man formal als .

1 Bestimmung mit dem Taschenrechner
Kubikwurzeln ermittelte man früher mit Tabellen, heute gibt es dafür Taschenrechner. 
Mit dem TI30 z.B. geht man so vor:
Nach Eingabe der betreffenden Zahl drückt man die Tasten yx , (1/3) und schließt mit = ab.
Beispiel: [2299968] -- [yx] -- [(1/3)] --  [=] . Man erhält 22999681/3 =132. 
Noch einfacher ist es, bei Google im Suchfeld 2299968^(1/3) einzugeben. 
Nach Drücken der Eingabetaste erscheint die Kubikzahl.
2 Bestimmung über eine Intervallschachtelung
22999681/3
Die Zahl muss zwischen 100 und 200 liegen (100³=1000000, 200³=8000000).
Die Zahl liegt zwischen 130 und 140 (130³=2197000 und 140³=2744000).
Sie muss nahe an 130 liegen und zur Einerziffer 8 führen. Da kommt 132 in Frage.
Ergebnis:  22999681/3=132 
3 Bestimmung über eine Faktorenzerlegung
22999681/3
Man zerlegt die Zahl in Faktoren und entwickelt daraus die Kubikzahl.
2299968  =  8*287496  =  8*27*10648 =  8*27*8*1331=8*27*8*11*121=8*8*27*11³=(2*2*3*11)³=132. 
Ergebnis:  22999681/3 = 132.

Dritte Wurzeln aus negativen Zahlen?     top
Es gilt (-2)³=-8. Daraus könnte man folgern, dass dann (-8)1/3=-2 gilt. Diese Schreibweise war früher (auch in der Schule) durchaus üblich. Heute verlangt man, dass a1/3 nur für a>0 oder a=0 definiert ist, dass also (-8)1/3 gar nicht erst zugelassen  wird. Man vermeidet so Widersprüche, wie die folgende Rechnung zeigt.
Es gilt (-8)1/3=(-8)2/6=[(-8)2]1/6=(64)1/6=(26 )1/6=2.
Das hieße, dass (-8)1/3 nicht eindeutig definiert wäre. Je nach Rechenweg erhielte man unterschiedliche Ergebnisse.

Das allerdings ist möglich:
Die Gleichung (-2)³=-8 wird umgeschrieben zu -(81/3)=-2. Allgemein führt x³=a für a<0 zu x=-(-a)1/3.

Folgen und Reihen top
Reihe der Kubikzahlen
Zu jeder Folge gibt es eine Reihe, nämlich die Folge der Partialsummen.
Das ist für die Kubikzahlen die Folge mit sn= 1³+2³+3³+...+n³. 
Es gilt 1³+2³+3³+...+n³=[n(n+1)/2]²

Beweis der Formel über die vollständige Induktion
>Die Formel trifft zu für n=1:     s1=[1*(1+1)/2]²=1
>Die Formel gelte für n:  sn=[n(n+1)/2]².
>Dann ist zu zeigen, dass sie auch für n+1 gilt: sn+1 = [(n+1)(n+2)/2]².
>Rechnung
Der Term [(n+1)(n+2)]² wird vorweg in eine Summe verwandelt.
[(n+1)(n+2)]²=(n²+3n+2)²=n4+(3n+2)²+2n²(3n+2)=n4+(9n²+12n+4)+(6n³+4n²)=n4+6n³+13n²+12n+4
Es gilt 
sn+1 = sn+(n+1)³ = [n(n+1)/2]²+(n+1)³ = [n²(n+1)²+4(n+1)³]/4 = [n²(n²+2n+1)+(4n³+12n²+12n+4)]/4 
= (n4+6n³+13n²+12n+4)/4 = [(n+1)(n+2)]²/4 = [(n+1)(n+2)/2]², wzbw..
In der Formel sn=[n(n+1)/2]² steckt die Reihe der natürlichen Zahlen. Für sie gilt nämlich 1+2+3+ ...+n=n(n+1)/2.
Es gilt damit die Beziehung 1³+2³+3³+...+n³ = (1+2+3+...+n)²,
die rechts veranschaulicht wird.
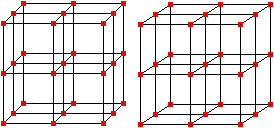
Deutung als arithmetische Folge 3. Ordnung
Die Folge der Kubikzahlen bezeichnet man auch als arithmetische Folge 3. Ordnung. 
Zur Erklärung folgt eine Figur.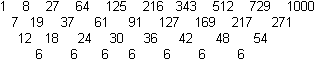
In jeder neuen Zeile steht die Differenz der beiden darüber liegenden Zahlen. Das Kennzeichnende ist, dass man in drei Schritten zur konstanten Differenz 6 gelangt. 
Es gibt für diese Folgen Formeln, mit deren Hilfe man 1³+2³+3³+...+n³=[n(n+1)/2]² auch herleiten kann. Das kann man in der Facharbeit von Steffen Weber (URL unten) nachlesen.
Reihe aus ungeraden Zahlen
Es gilt 1³=1, 2³=3+5, 3³=7+9+11, 4³=13+15+17+19, ...
Dann ist 1³+2³+3³+4³+... = 1+3+5+7+9+11+13+15+17+19+...
Reihe der reziproken Kubikzahlen
Es gibt eine weitere Reihe aus Kubikzahlen, die der Kehrwerte: 1/1³+1/2³+1/3³+...+1/n³.
Sie ist konvergent. Auf der de.wikipedia-Seite findet man den Grenzwert, die riemannschen Zeta-Funktion an der Stelle 3.
Reihe der zentrierten Sechseckszahlen
Die Folge der zentrierten Sechseckszahlen ist 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, ...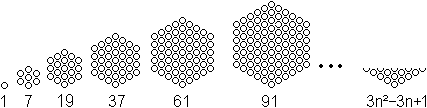
Das Bildungsgesetz ist an=3n²-3n+1.
Es gilt 1, 1+7=8, 1+7+19=27, 1+7+19+37=64, ...
Die Reihe zur Folge der zentrierten Sechseckszahlen ist die Folge der Kubikzahlen.
Rechnung dazu: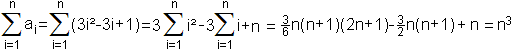

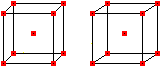
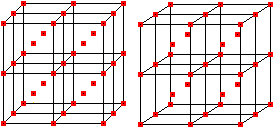
Dabei werden die Formeln 1²+2²+3³+...+n²=(1/6)n(n+1)(2n+1) und 1+2+3+...+n=(1/2)n(n+1) verwendet.
Folge der zentrierten Kubikzahlen
Die Folge der zentrierten Kubikzahlen ist 1, 9, 35, 91, 189, 341, 559, 855, 1241,...

...1...

 

9
.

35
Die Bildpaare ermöglichen eine 3-D-Ansicht.

Das Bildungsgesetz ist an=2n³-3n²+3n-1. 
Addiert man zwei aufeinander folgende Kubikzahlen, entstehen die zentrierten Kubikzahlen.
Es gilt 2n³-3n²+3n-1=n³+(n -1)³ 

Das Atomium in Brüssel, ein raumzentrierter Würfel
...... Das Bauwerk ist 102 Meter hoch und besteht aus neun Kugeln von jeweils 18 Meter Durchmesser. 

Die Kugeln verbinden 23 Meter lange Röhren mit einem Durchmesser von 3,3 Metern. 

Aufnahme von Juli 2011
Folge der vollkommenen Zahlen
T.L. Heath (1861-1940) bewies, dass jede gerade vollkommene Zahl - ausgenommen 6 - als Summe von 2(n-1)/2 Kubikzahlen dargestellt werden kann, zum Beispiel 
28=1³+3³,
496=1³+3³+5³+7³,
8128=1³+3³+5³+7³+9³+11³+13³+15³.
Quelle (3) Seite 14f.

WARINGsches Problem       top
Der englische Mathematiker Eduard Waring (1734-1798) stellte u.a. die folgende Behauptung auf.
"Jede ganze Zahl ist entweder eine Kubikzahl oder die Summe von 2,3,4,5,6,7,8 oder 9 Kubikzahlen." 
(2), Seite 37ff.

Das bedeutet, dass 9 eine Mindestanzahl ist. 
Es können natürlich auch mehr als neun sein, wie die folgende Zerlegung von 180³ in 64 Summanden zeigt. 
180³ = 6³+7³+8³+...+67³+68³+69³ (1). Man kommt mit 4 Summanden aus, 180=1³+3³+3³+5³.
Die ersten Zahlen
1=1³
2=1³+1³
3=1³+1³+1³
4=1³+1³+1³+1³
5=1³+1³+1³+1³+1³ 
6=1³+1³+1³+1³+1³+1³
7=1³+1³+1³+1³+1³+1³+1³ 
15=2³+1³+1³+1³+1³+1³+1³+1³ 
23=2³+2³+1³+1³+1³+1³+1³+1³+1³ 
Zerlegungen der Zahlen bis 100, ermittelt mit einem einfachen Computerprogramm.
Die Mindestanzahl der Summanden ist bestimmend. 
>Summe aus mindestens 2 Kuben benötigen die Zahlen 2, 9, 16, 28, 35, 54, 65, 72, 91 
>Summe aus 3 Kuben: 3, 10, 17, 24, 29, 36, 43, 55, 62, 66, 73, 80, 81, 92, 99 
>Summe aus 4 Kuben:4, 11, 18, 25, 30, 32, 37, 44, 51, 56, 63, 67, 70, 74, 82, 88, 89, 93, 100 
>Summe aus 5 Kuben: 5, 12, 19, 26, 31, 33, 38, 40, 45, 52, 57, 59, 68, 71, 75, 78, 83, 90, 94, 96, 97 
>Summe aus 6 Kuben: 6, 13, 20, 27, 34, 39, 41, 46, 48, 53, 58, 60, 69, 76, 79, 84, 86, 95, 98 
>Summe aus 7 Kuben: 7, 14, 21, 42, 47, 49, 61, 77, 85, 87 
>Summe aus 8 Kuben für 15, 22, 50 
(Alle Zahlen sind 15, 22, 50, 114, 167, 175, 186, 212, 231, 238, 303, 364, 420, 428, 454.)
>Summe aus 9 Kuben für 23, (und nur noch 239)
>Kubikzahlen unter 100 sind 8, 27, 64
Eine Anekdote gibt es zu den Zerlegungen 1729=1³ + 12³ und 1729= 9³ + 10³, nachzulesen auf der Wikipedia-Seite Tausendsiebenhundertneunundzwanzig. (URL unten)
Summe von Kuben
Für Quadratzahlen führt die Gleichung x²+y²=z² zu den pythagoräischen Zahlen (mehr auf meiner Seite 3-4-5-Dreieck).
Die verallgemeinerte Gleichung xn+yn=zn hat für n>2 keine Lösung. Das ist das berühmte große Fermatproblem.  Die Unlösbarkeit wurde erst 1993/95 von Andrew Wiles und Richard Taylor bewiesen. Wie es dazu kam, ist nachzulesen im faszinierenden und empfehlenswerten Buch von Simon Singh (4).
Wenn sich also eine Kubikzahl nicht als Summe zweier Kubikzahlen darstellen lässt, so kann man Zerlegungen mit drei und mehr Kuben suchen.
Ein schönes Beispiel ist 3³+4³+5³=6³, zumal die Grundzahlen auch noch aufeinander folgen.
Weitere Beispiele finden sich im Kapitel Zahlenspielereien unten.

Besondere Kubikzahlen top
Quadratzahlen unter den Kubikzahlen 
Es gibt Kubikzahlen, die auch Quadratzahlen sind. 
Man kann sie der Reihe nach konstruieren, indem man die Kubikzahlen quadriert.
23 führt zu 26=64, 33 zu 36=729, 4³ zu 46=4 096, ...
Weitere Kubikzahlen und gleichzeitig Quadratzahlen unter 1 000 000 sind 1, 15 625, 46 656, 117 649, 262 144 und 531 441.

Palindrome unter den Kubikzahlen 
343=7³
131=11³, 1030301=101³, 1003003001=1001³, ...
1367631=111³, 1030607060301=10101³, 1003006007006003001=1001001³, ...
1334996994331=11011³, 1331399339931331=110011³, ... 
1033394994933301=1011010³, ...
Es fällt auf, dass die Grundzahlen auch Palindrome sind. 
Nach Martin Gardner ist 10662526601 = 2201³ das einzige Palindrom mit einer nichtpalindromischen Grundzahl.
Quelle: Patrick De Geest  (World!of numbers)

Zahlenspielereien top
In diesem Kapitel werden u.a. Ergebnisse aus Lietzmanns Buch (1) von 1948 zusammengestellt und mit Computerhilfe überprüft und ergänzt. 
Eine Kubikzahl ist gleich der dritten Potenz ihrer Quersumme.
512=8³=(5+1+2)³ 
4913=17³=(4+9+1+3)³ 
5832=18³=(5+8+3+2)³ 
17576=26³=(1+7+5+7+6)³ 
19683=17³=(1+9+6+8+3)³ 

Eine Zahl ist die Summe der dritten Potenzen ihrer Ziffern.
153=1³+5³+3³
370=3³+7³+0³
371=3³+7³+1³
407=4³+0³+7³

Das fand das nebenstehende, einfache Programm.

 for x=0 to 9
for y=0 to 9
for z=0 to 9
if x*x*x+y*y*y+z*z*z=100*x+10*y+z then print x,y,z
next z
next y
next x
Variationen
22+2=2³+2³+2³

12*3=1³+2³+3³
32*5=3³+2³+5³
50*5=5³+0³+5³
51*3=5³+1³+3³

 151+3=1³+5³+1³+3³ und 153+1
370+1=3³+7³+0³+1³
371+1=3³+7³+1³+1³
400+7=4³+0³+0³+7³
401+7=4³+0³+1³+7³ und 407+1=4³+0³+1³+7³ 
464+5=4³+6³+4³+5³ und 465+4=4³+6³+4³+5³ 
624+7=6³+2³+4³+7³ und 627+4=6³+2³+4³+7³
643+7=6³+4³+3³+7³ und 647+3=6³+4³+3³+7³
733+7=7³+3³+3³+7³ und 737+3=7³+3³+3³+7³ 
773+4=7³+7³+3³+4³ und 774+3=7³+7³+3³+4³ 
914+5=9³+1³+4³+5³ und 915+4=9³+1³+4³+5³ 		 12+32=1³+2³+3³+2³ 
20+23=2³+0³+2³+3³ 
21+23=2³+1³+2³+3³ 
30+32=3³+0³+3³+2³ 
31+32=3³+1³+3³+2³ 

107*8=1³+0³+7³+8³
180*3=1³+8³+0³+3³
989*2=9³+8³+9³+2³
18*30=1³+8³+3³+0³
Terme mit gleichen Ziffern 
3³+7³=37*(3+7)
4³+8³=48*(4+8)
14³+7³=147*(14+7)
14³+8³=148*(14+8) 
Kubikzahlen werden mit den Ziffern 1 bis 9 dargestellt. Jede Ziffer kommt genau einmal vor.
125*438976=380³
8*24137569=578³
8*32461759=628³
Zwei Zahlen mit gemeinsamen Eigenschaften
Beispiele
24³=13824 und 76³=438976 
25³=15625 und 75³=421875
49³=117649 und 51³=132651
125³=1953 125 und 875³=669921875
251³=15813251 und 749³=420189749

0624³ = 242970624 und 9376³ = 824238309376
0625³ = 244140625 und 9375³ = 823974609 375

21952 = (6+8+5+9)³ und 6859 = (2+1+9+5+2)³ 

 Erklärungen
24+76=100, 13824 und 438976
25+75=100, 15625 und 421875
49+51=100, 117649 und 132651
125+875=1000, 1953125 und 669921875
251+749=1000, 15813251 und 420189749

0624+9376=10000, 242970624 und 824238309 376
0625+9375=10000, 244140625 und 823974609 375

21952 und 2+1+9+5+2, sowie 6+8+5+9 und 6859
Die Grundzahlen bilden arithmetische Folgen
180³ = 6³+7³+8³+...+67³+68³+69³
540³ = 34³+35³+ ... +158³
2856³ = 213³+214³+ ... +555³
5544³ = 406³+407³+ ... +917³ 
16830³ = 1134³+1135³+ ... +2133³
3990³ = 290³+293³+ ... +935³
29880³ = 2108³+2111³+ ... +4292³
408³ = 149³+256³+363³
440³ = 230³+243³+265³+269³+282³
1155³ = 435³+506³+577³+648³+719³+790³
2128³ = 553³+710³+867³+1024³+1181³+1338³+1475³
168³ = 28³+41³+54³+67³+80³+93³+106³+119³
64085³ = 935³+5868³+10801³+15734³+20667³+25600³+30533³+35466³+40399³+45332³
495³ = 15³+52³+89³+B6³+163³+200³+237³+274³+311³+248³

Kubikzahlen im Internet  top

Deutsch

Steffen Weber (Facharbeit im Leistungskurs Mathematik)
Partialsummen und Zahlenfolgen

Wikipedia
Kubikzahl, Zentrierte Kubikzahl,  Zentrierte Sechseckszahl,  Tausendsiebenhundertneunundzwanzig


Englisch

Eric W. Weisstein (MathWorld)
Cubic Number, Centered Cube Number, Cuban Prime,  Cubic Triangular Number

N. J. A. Sloane  (On-Line Encyclopedia of Integer Sequences) 
Integer Sequences
The cubes A000578,
Waring's problem A018888, 
Centered cube numbers  A005898
Hex (or centered hexagonal) numbers  A003215
The only integers equal to the sum of the digits of their cubes A046459
Numbers that are the sum of 2 positive cubes A003325
Numbers that are the sum of 3 positive cubes  A003072
Numbers that are the sum of 4 but no fewer positive cubes A003072
Numbers that are the sum of 5 but no fewer positive cubes A003328
Numbers that are the sum of 6 positive cubes  A003329
Smallest expression as sum of positive cubes requires exactly 7 cubes A018890
Shortest representation as sum of positive cubes requires exactly 8 cubes  A018889

Patrick De Geest (World!of Numbers)
Palindromic Cubes

Wikipedia
Cube (algebra), Centered cube number,  Centered hexagonal number,  1729 (number)

Referenzen   top
(1) Walter Lietzmann: Sonderlinge im Reich der Zahlen, Bonn 1948
(2) Rademacher-Toeplitz: Von Zahlen und Figuren, Springer, Berlin, Heidelberg, New York1968 (Nachdruck von 1930) 
(3) Maximilian Miller: Gelöste und ungelöste mathematische Probleme, Leipzig 1973 
(4) Simon Singh: Fermats letzter Satz, dtv 33052, München 2000 [ISBN 3-423-33052-X]
(5) Singh, Simon: Fermat's Last Theorem. Fourth Estate, 1997  [ISBN 1-85702-669-1]

 Feedback: Emailadresse auf meiner Hauptseite

Diese Seite ist auch in Englisch vorhanden

URL meiner Homepage:
https://www.mathematische-basteleien.de/

©  2009 Jürgen Köller

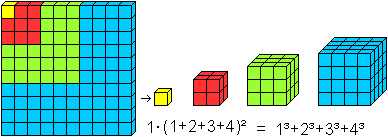
top