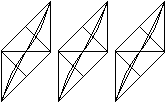|
Was ist eine dreiseitige Pyramide?
... ... ...
|
... ... ... |
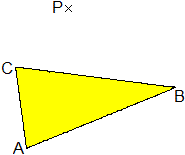
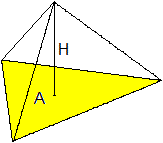
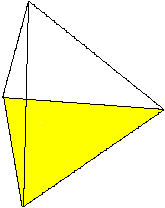
Gegeben sei ein beliebiges Dreieck ABC und ein Punkt
P, der nicht in der Ebene des Dreiecks liegt. Verbindet man diesen Punkt
mit den Eckpunkten des Dreiecks, so entsteht eine dreiseitige
Pyramide oder eine Dreieckspyramide. |
Der Einfachheit halber heißt
die dreiseitige Pyramide auf dieser Webseite einfach Pyramide.
... ...J ...J
|
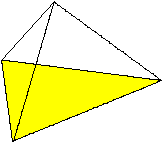
Wie jede Pyramide hat die dreiseitige Pyramide eine Grundfläche,
eine Spitze, Seitenflächen und eine Höhe.
Diese Pyramide hat vier Seitenflächen, sechs Kanten
und vier Ecken. In jedem Eckpunkt treffen drei Kanten aufeinander.
Jede Seitenfläche kann auch Grundfläche sein.
Man bevorzugt die Lage, bei der die Höhe innerhalb der Pyramide liegt. |
...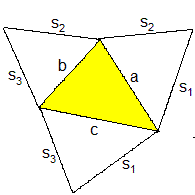 ... ... |
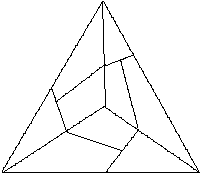
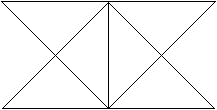
Klappt man die Seitenflächen in die Ebene des Grunddreiecks,
so erhält man ein Netz der Pyramide.
Da die Seitenflächen jeweils eine Seite gemeinsam
haben, wird das Netz durch je eine Seite eines Seitendreiecks und durch
die drei Seiten des Grunddreiecks bestimmt.
Sechs Strecken bestimmen die Pyramide. |
Auf dieser Webseite werden der Reihe nach besondere Pyramiden
besprochen.
Oberfläche
und Volumen top
... ... ...
|
Angenommen, man kennt die Grundfläche A und die
Höhe h der Pyramide.
Das Volumen ist dann wie bei jeder Pyramide V=(1/3)AH. |
... ... ... |
Eine Pyramide wird bestimmt durch sechs Größen.
Das können die Seiten der Dreiecke sein, die oben
eingeführt wurden.
Dann ist die Oberfläche die Summe der Flächeninhalte
der vier Dreiecke.
Für das Grunddreieck gilt die heronsche Formel A=sqrt[s(s-a)(s-b)(s-c)]
mit s=(1/2)(a+b+c).
Entsprechende Formeln gelten für die Seitenflächen.
Eine Formel für das Volumen müsste es theoretisch
auch geben. Sie ist mir nicht bekannt. |
...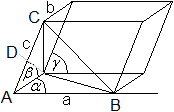 ... ... |
Man kann die Pyramide auch durch drei Kanten a, b und
c sowie die Winkel alpha, beta und gamma zwischen den Kanten eindeutig
beschreiben. Das sind wieder sechs Größen. Dann gilt für
die Pyramide ABCD
V=(1/6)abc*sqrt[1 + 2cos(alpha)cos(beta)cos(gamma)-cos²(alpha)-cos²(beta)-cos²(gamma)].
Die Formel wird im Wesentlichen auf meiner Webseite Parallelepiped
hergeleitet.
Auf eine Formel für die Oberfläche verzichte
ich. |
Tetraeder
top
... ... ...
|
... ... ...
|
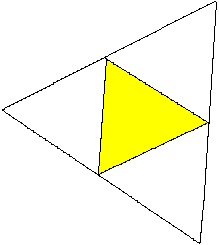
Hat die Pyramide sechs gleich lange Kanten oder wird
die Pyramide aus vier gleichseitigen Dreiecken gebildet, so handelt es
sich um ein Tetraeder.
Mehr auf meiner Seite Tetraeder |
Man bezeichnet die allgemeine
Dreieckspyramide auch als Tetraeder. Das ist berechtigt, denn Tetraeder
heißt Vierflächner.
Dann muss man für das Tetraeder
regelmäßig
hinzufügen.
Aber meist verwendet man wie ich auf dieser Webseite
die Bezeichnungen
dreiseitige Pyramide für die allgemeine,
Tetraeder
für die regelmäßige, dreiseitige Pyramide.
Im englischen Sprachbereich gibt es die gleichen Unklarheiten
mit triangular pyramid und tetrahedron bzw. tetrahedron
und regular tetrahedron.
Pyramiden im Quader
top
Die folgenden Bildpaare ermöglichen
eine räumliche Sicht.
...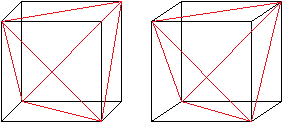 ... ... |
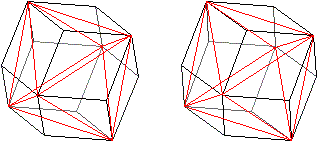
Verbindet man vier passende Eckpunkte eines
Würfels
in bestimmter Weise, entsteht ein Tetraeder. |
...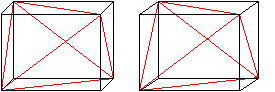 ... ... |
Verbindet man vier passende Eckpunkte eines Quaders,
so entsteht eine Pyramide.
Sie wird von Flächendiagonalen des Würfels
gebildet. Hat der Quader verschieden lange Kanten, so sind auch die Flächendiagonalen
verschieden lang. Dennoch ist es keine allgemeine Pyramide, die Gegenkanten
sind gleich lang und orthogonal. |
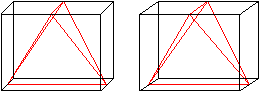 |
Verbindet man vier passende Kantenmitten eines Quaders
in bestimmter Weise, entsteht ein Pyramide.
Je zwei Dreiecke sind kongruent und gleichschenklig,
ein Paar Gegenkanten ist orthogonal. |
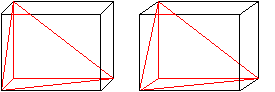 |
Verbindet man vier bestimmte Eckpunkte eines Quaders,
so entsteht eine dreiseitige Pyramide mit drei rechten Winkeln in einem
Eckpunkt.
Diese "rechtwinklige" Pyramide wird unten untersucht. |
Gerade
Dreieckspyramide top
... ... ...
|
... ... ... |
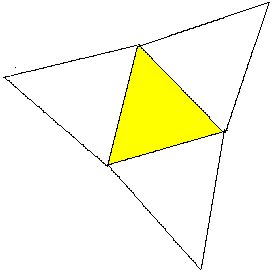
Ist die Grundfläche ein beliebiges Dreieck und sind
die Seitenflächen gleichschenklige Dreiecke, so handelt es sich um
eine gerade dreiseitige Pyramide. - Die Spitze liegt über dem Schwerpunkt
des Dreiecks.
Ist darüberhinaus das Grunddreieck gleichseitig und
sind die Seitenflächen gleichschenklig wie hier, so spricht man von
der regelmäßigen dreiseitigen Pyramide. |
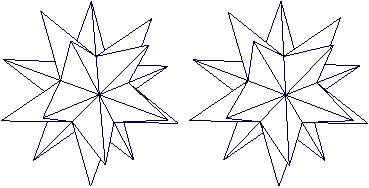
Es gibt zahlreiche dreidimensionale
Sterne, die dadurch entstehen, dass man auf passende Polyeder gerade Dreieckspyramiden
setzt. Sie heißen Zacken. Auf meiner Webseite zum Basteln des
Bascetta-Sterns gibt es ein Kapitel Bekrönte
Polyeder.
Ich habe vier Stereobilder und zwei Fotos herausgezogen.
Disphenoid
top
... ... ...
|
... ... ...
|
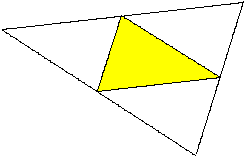
Zeichnet man in ein beliebiges Dreieck das Mittendreieck,
so entsteht das Netz des Disphenoids. (nach altgriechisch sphenoid, „Keil“).
Die Grundfläche und die drei Seitenflächen
sind kongruente Dreiecke.
In Anlehnung an die englische Bezeichnung Isosceles
Tetrahedron heißt es auch gleichschenkliges Tetraeder. |
...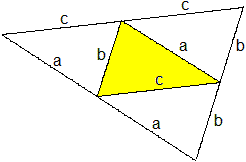 |
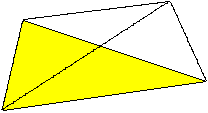
In der Zeichnung erhalten alle Strecken einen Namen.
So kann man einsehen, dass die gegenüberliegenden
Kanten gleich lang sind. |
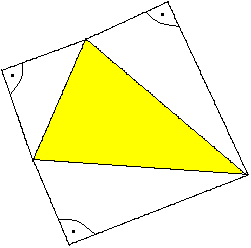
Rechtwinklige
Pyramide top
Darunter verstehe ich in Anlehnung
an die englische Bezeichnung Trirectangular tetrahedron eine
Pyramide mit drei rechten Winkeln an der Spitze.
Netz
und Schrägbild der Pyramide mit beliebigem Dreieck
... ... ...
|
 ... ... |
Die Grundfläche sei ein beliebiges Dreieck und die
Seitenflächen rechtwinklige Dreiecke. |
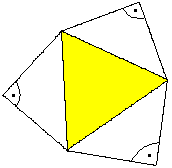
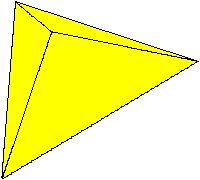
Netz
und Schrägbild der Pyramide mit gleichseitigem Dreieck
... ... ...
|
... ... ...
|
Die Seitenflächen sind gleichschenklig-rechtwinklig. |
Pyramiden
im Quader und Würfel
Eine Zugang zu diesen Pyramiden erhält man, wenn
man in einem Quader bzw. Würfel vier passende Eckpunkte miteinander
verbindet.
... ... ...
|
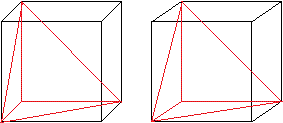
|
Rechtwinklige
Pyramide mit gleichseitigem Dreieck top
Modell
... ... ... |
Man erhält ein einfaches Modell dieser Pyramide,
wenn man ein Quadrat ausschneidet, längs einer halben Diagonalen einschneidet
und die beiden grünen Dreiecke aufeinanderlegt. |
Rechnungen
...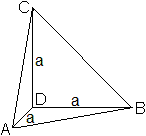 ... ... |
Die Pyramide ABCD im Würfel wird durch eine Größe
bestimmt, z.B. durch die Kantenlänge a des Würfels bzw. die Seitenkante
a der Pyramide.
Das Dreieck ABC ist gleichseitig und hat die Seitenlänge
sqrt(2)a. |
Oberfläche
Die Oberfläche der Pyramide ist O = 3As+Ag,
As = (1/2)a² ist der Flächeninhalt
einer Seitenfläche,
Ag = (1/4)(sqrt3)[(sqrt(2)a)]² = (1/4)(sqrt3)2a²
= (1/2)sqrt(3)a² der der Grundfläche.
Dann ist O = 3*(1/2)a²+(1/2)sqrt(3)a² oder
O
= (1/2)[3+sqrt(3)]a².
... |
Weiter gilt Ag²
=
(3/4)a4 = 3*(1/4)a4 = 3As².
........................................ |
Die
Verallgemeinerung für beliebige rechtwinklige dreiseitige Pyramiden
ist Ag² =As1² + As2²
* As3² (Satz von de Gua).
Dabei sind s1, s2 und s3
die Seitenkanten der Pyramide.
Quelle: Trirectangular tetrahedron (MathWorld,
URL unten)
Volumen
1.Herleitung
...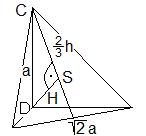 ... ... |
Das Volumen ist V = (1/3)AgH.
Die Raumhöhe H findet man im rechtwinkligen Dreieck
CDS mit den Seiten H, (2/3)h und a
mit h=(1/2)sqrt(3)*sqrt(2)a = (1/2)sqrt(6)a.
|
Nach dem Satz des Pythagoras gilt H² = a²-
[(2/3)h²] = a²-(2/3)a² = (1/3)a².
Dann ist H = (1/3)sqrt(3)a.
Dann ist V = (1/3)*(1/2)sqrt(3)a²*(1/3)sqrt(3)a
oder V= (1/6)a³.
2.Herleitung
Man betrachtet ein gleichschenklig-rechtwinkliges Dreieck
als Grundfläche. Dann V=(1/3)A'H = (1/3)*(1/2)a²*a oder V
= (1/6)a³.
Die
Verallgemeinerung für beliebige rechtwinklige dreiseitige Pyramiden
lautet V = (1/6)abc.
Dabei sind a, b und c die Seitenlängen
der rechtwinkligen Pyramide.
Das aber ist die Formel
V=(1/6)abc*sqrt[1 + 2cos(alpha)cos(beta)cos(gamma)-cos²(alpha)-cos²(beta)-cos²(gamma)]
für alpha = beta = gamma = 90°.
Beaded Origami
Ornament (Mit Perlen versehenes Origami-Ornament) top
... ... ...
|
... ... ...
|
Spiegelt man die rechtwinklige Pyramide an der Grundfläche,
entsteht eine Bipyramide aus sechs gleichschenklig-rechtwinkligen Dreiecken. |
Diese Bipyramide erwähne
ich, um auf eine hübsche Bastelei hinzuweisen.
Man kann sie aus drei Sonobe-Modulen flechten.
Auf meiner Webseite Körper flechten erkläre
ich, wie man aus sechs Modulen einen Würfel flechtet. Die Bipyramide
ist ähnlich herzustellen. Man bildet zuerst eine Spitze (beim Würfel
eine Ecke) aus drei rechtwinkligen Dreiecken. Dabei beachtet man, dass
die glatte Seite innen liegt. Aus den frei hängenden Spitzen formt
man die Gegenpyramide.
Mehr im Kapitel Sonobe-Würfel
auf meiner Webseite Körper flechten und auf meiner Webseite
Sonobe-Stern.
Dreiseitige
Pyramide im Internet top
Deutsch
Michael Buhlmann
Dreiseitige
Pyramide (Applet)
Rudolf Fritsch
Winkelverteilung
am Tetraeder (.pdf-Datei)
Wikipedia
Tetraeder,
Disphenoid,
Pyramide
(Geometrie)
Englisch
Eric W. Weisstein (MathWorld)
Tetrahedron,
Regular
Tetrahedron, Isosceles
Tetrahedron, Trirectangular
tetrahedron, Triangular
bipyramid
TechnologyUK
The
Tetrahedron
Wikipedia
Tetrahedron,
Disphenoid,
Trirectangular
tetrahedron, Pyramid,
Triangular
bipyramid,
Sonobe,
Euler
brick
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© 2015 Jürgen Köller
top |
 ...
... ...
... ...J
...J ...
... ...
... ...
... ...
... ...
... ...
...

 ...
... ...
...
 ...
...



 ...
... ...
...
 ...
... ...
... ...
...
 ...
... ...
...
 ...
... ...
... ...
...