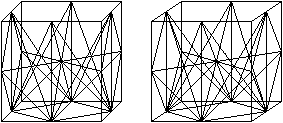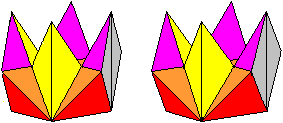Was ist Cube One ?
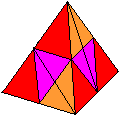
Das Ziel ist es, aus vier 16-gliedrigen Ketten von Dreieckspyramiden
(Kaleidozyklen) einen Würfel zu bauen.
Zeichnerisch dargestellt:
Die Farben, die ich in den Zeichnungen verwende, entstammen dem Puzzle. Untersuchung
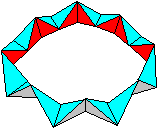
der Oktaeder-Kette top
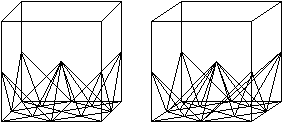
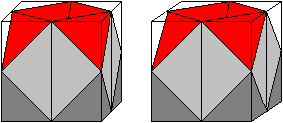
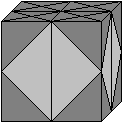
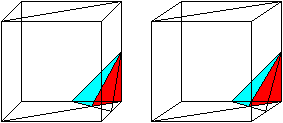
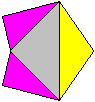
Entstehung der Pyramide Rot/Blau Die Ecke eines Würfels bildet eine Pyramide, wenn man drei Kantenmitten miteinander verbindet. Legt man durch den Würfel noch eine Schnittebene in Diagonalenrichtung, so wird der Eckenkörper halbiert. Der Halbkörper ist eine Pyramide der Oktaeder-Kette. Die Lage kann mit in einer Stereo-Zeichnung erkennen:
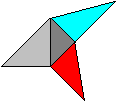
Volumen Die Pyramide hat das kleine graue Dreieck als Grunddreieck und die Höhe a/2. Das Volumen V1' ist (1/3)*[(1/2)(a/2)*(a/2)/2]*(a/2)=a³/96. Die Oktaeder-Kette hat Volumen V1= 16V1' =16a³/96=a³/6. Untersuchung
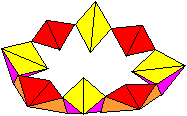
der Tetraeder-Kette
top
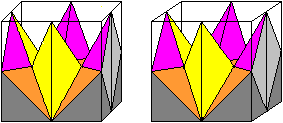
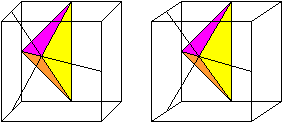
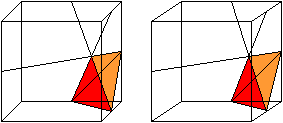
Entstehung der 1.Pyramide (Violett/Gelb) Die Pyramiden entstehen, wenn man in einem Würfel gewisse Kantenmitten miteinader verbindet. Die Lage kann man in einer Stereo-Zeichnung erkennen.
Maße der Pyramide
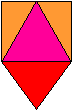
Volumen Die Pyramide hat das gelbe Dreieck als Grunddreieck und die Höhe sqrt(6)/4*a. Das Volumen V21' ist (1/3)*[(a/2)*(sqrt(2)/4*a]*(sqrt(2)/4*a)=a³/48. Entstehung der 2.Pyramide (Rot/Orange) Die Pyramiden entstehen, wenn man in einem Würfel gewisse Kantenmitten miteinader verbindet. Die Lage kann man wieder in einer Stereo-Zeichnung erkennen.
Maße der Pyramide
Volumen Die Pyramide hat das rote Dreieck unten als Grunddreieck und die Höhe sqrt(2)/4*a. Das Volumen V22' ist (1/3)*[(a/2)*(sqrt(2)/4*a]*(sqrt(2)/4*a)=a³/48. Volumen der Tetraeder-Kette Die Tetraederkette besteht aus acht Pyramiden Violett/Gelb und acht Pyramiden Rot/Orange. Damit gilt für das Volumen: V2=8*V21' + 8V22' = 8a³/48+8a³/48=a³/3. Aufteilung des Würfels Das Volumen V des Würfels verteilt sich auf die einzelnen Ketten wie folgt.
Lösung von Cube
One
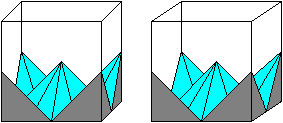
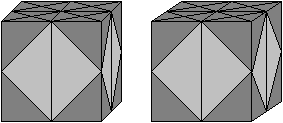
Diese Figur legt man in den durchsichtigen, oben offenen Plastikwürfel, der zum Lieferumfang des Puzzles gehört.
Die Krone legt man auf die Oktaederkette in den Würfel.
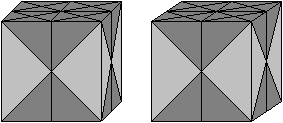
Dritter Schritt Aus der Tetraederkette bildet man eine zweite Krone und stülpt sie auf die erste.
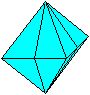
Man schließt den Würfel mit einem zweiten aufgeklappten Oktaeder.
Zweite Lösung Nach Angabe des Erfinders gibt es noch eine weitere Lösung. Der fertige Würfel hat dann folgendes Aussehen.
Mehr über Kaleidozyklen findet man an anderen Stellen meiner Homepage: Kaleidozyklen, The Shinsei Miracle Cube One im Internet top Dieter A.W. Junker
Feedback: Emailadresse auf meiner Hauptseite Diese Seite ist auch in Englisch vorhanden. URL meiner
Homepage:
© 2006 Jürgen Köller |

 ...
...
 ...
...