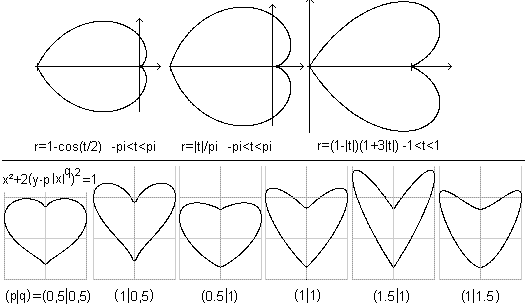|
Was ist die Betragsfunktion?
Jeder reellen Zahl ist ein (absoluter) Betrag |x| zugeordnet.
Diese Zuordnung f mit f(x)=|x| heißt Betragsfunktion.
... ... ... |
Jede reelle Zahl hat einen Platz auf der Zahlengeraden.
Der Betrag |x| einer Zahl ist die Entfernung der Zahl vom Nullpunkt. Zahl
und Gegenzahl haben den gleichen Betrag. |
Der Funktionsterm wird abschnittsweise
definiert.
...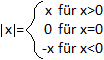 ... ... |
Es verwirrt vielleicht, dass in der dritten Zeile vor
x ein Minuszeichen steht.
Es gilt trotzdem -x>0, denn dahinter steckt "-(-a)=a". |
In Programmiersprachen wird der Funktionsterm
|x| mit abs(x) bezeichnet.
Eigenschaften top
Graph
...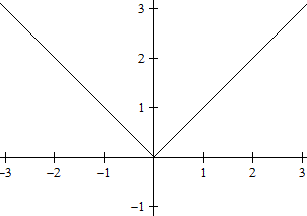 .... ....
|
Der Graph besteht aus zwei Halbgeraden im 1. und 2. Quadranten.
Das sind die 1. und 2. Winkelhalbierende im Koordinatensystem.
Im Nullpunkt liegt eine Knickstelle, in der keine eindeutige
Steigung definiert werden kann.
Der Graph ist achsensymmetrisch bezüglich der y-Achse,
denn es gilt f(x) = f(-x).
Ich bezeichne ihn auf dieser Webseite als V-Linie. |
Ableitung
...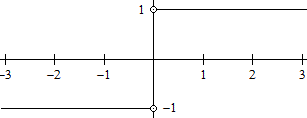 ... ... |
Die Ableitung gibt die Steigung des Graphen der Betragsfunktion
an. Die beiden Halbgeraden haben die Steigung +1 und -1. Das führt
zum nebenstehenden Graphen.
Der Funktionsterm könnte sein: f '(x)=|x|/x.
Die problematische Stelle x= 0 muss man herausnehmen.
Das beschreibt man durch die beiden hohlen Kreise bei y=1 und y=-1.
|
Signumfunktion
Die Signum- oder Vorzeichenfunktion
hält das Vorzeichen einer reellen Zahl fest.
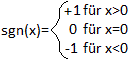
|
Graph
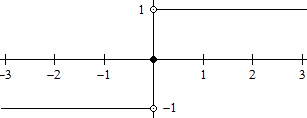
|
Die Signumfunktion ist im Grunde die Ableitungsfunktion,
nur dass hier auch die Stelle x=0 definiert ist.
Das markiert man durch ein Kreuz oder (wie hier) durch
einen ausgefüllten Kreis.
Mit
der Signumfunktion erhält man eine Schreibweise der Betragsfunktion,
in der Zahl und Vorzeichen getrennt sind: |x| = sign(x)*x.
Wurzel
Es gibt auch die Darstellung |x| = sqrt(x²). Darin
ist die Aussage enthalten, dass die Wurzel aus einer Zahl immer nichtnegativ
ist. Man schreibt also besser sqrt(x²) = |x|.
Allgemeine
Betragsfunktion top
V-Linie und Parabel
Die V-Linie erinnert an die Normalparabel. Auch sie hat
im Nullpunkt ein Minimum und ist symmetrisch zur y-Achse.
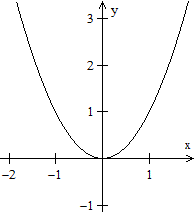
p(x)=x²
|
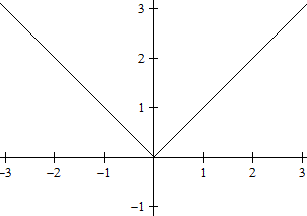
f(x)=|x|
|
Eine
Verallgemeinerung der Betragsfunktion erfolgt in zwei Schritten.
Schar von V-Linien
...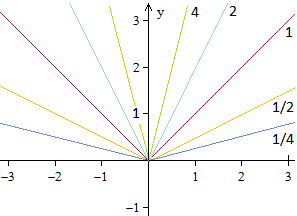 ... ... |
Wie bei der quadratischen Funktion mit
q(x)=ax² erhält man eine Schar von V-Linien, wenn man
f(x)=|x| auf f(x)=a|x| verallgemeinert. Die Variable a steht für eine
reelle Zahl außer 0. |
"Scheitelform"
...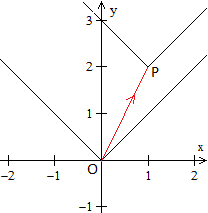 ... ... |
In einem nächsten Schritt verschiebt man die V-Linie
im Koordinatensystem.
Die Spitze in O(0|0) bewegt sich zu einem beliebigen
Punkt P(b|c).
Das führt zur allgemeinen Betragsfunktion f(x)=a|x-b|+c.
Für die Zeichnung gilt f(x)=|x-1|+2. |
Zwei
weitere Beispiele
| 2.Beispiel: f(x)=(1/2)|x-1|+2
Für x>1 gilt f(x)=(1/2)x+3/2
Für x=1 gilt f(x)=2
Für x<1 gilt f(x)=-(1/2)x+5/2 |
3. Beipiel f(x)=-|x+1|+2
Für x>-1 gilt f(x)=-x+1
Für x=-1 gilt f(x)=1
Für x<-1 gilt f(x)=x+3 |
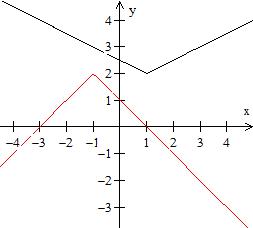
|
Darstellung
ohne Beträge
...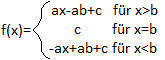 ... ... |
Dazu gibt man - ausgehend von der
allgemeinen Betragsfunktion f(x)=a|x-b|+c - eine abschnittsweise
definierte Darstellung an. So beseitigt man die Betragsstriche
durch
Fallunterscheidungen. |
Funktionen mit
Beträgen top
|f(x)| und f(|x|)
Man versieht gerne die Terme ganzrationaler Funktionen
f(x) mit Betragsstrichen. Dann erhält man einfache Beispiele stetiger,
aber nicht differenzierbarer Funktionen.
Die beiden Funktionen links stehen für die beiden
Haupttypen |f(x)| und f(|x|). Die rechte Funktion hat beide Eigenschaften.
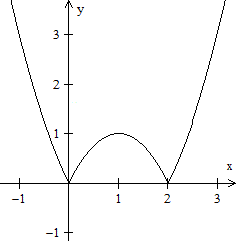
f(x) = |(x-1)²-1|
|

f(x)=(|x|-1)²+1/2
|
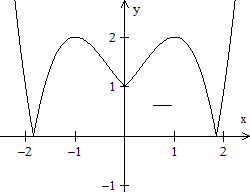
f(x) = |x²|x|-x²-|x|-1|
|
Die Bereiche des Graphen
von |f(x)|, die unterhalb der x-Achse liegen, werden nach oben geklappt.
Die Graphen von y=f(|x|) sind achsensymmetrisch bezüglich
der y-Achse.
Funktionsterme
mit ineinander geschachtelten Beträgen
Diskussion der Funktionsgleichung y=||x|-2|
Wegen einer besseren Darstellung lasse ich die Knickstellen
x=-2, x=0 und x=2 weg.
Ich verwende in den folgenden Überlegungen das Symbol
/\ für das logische "und".
Die Aussageformen rechts und links des Symbols /\ müssen
richtig sein.
Auflösen der inneren Betragsstriche
Fall I
x>0 /\ y=|x-2|
Fall II
x<0 /\ y=|-x-2|
Auflösen der äußeren
Betragsstriche
Fall Ia
x>0 /\ x>2 /\ y=x-2, zusammengefasst x>2
/\
y=x-2
Fall Ib
x>0 /\ x<2 /\ y=-x+2, zusammengefasst 0<x<2
/\
y=-x+2
Fall IIa
x<0 /\ -x-2>0 /\ y=-x-2, vereinfacht x<0 /\ x<-2
/\ y=-x-2, zusammengefasst x<-2 /\
y=-x-2
Fall IIb
x<0 und -x-2<0 /\ y=x+2, vereinfacht x<0 /\
x>-2 /\ y=x+2, zusammengefasst 0<x<-2 /\
y=x+2
Ergebnis
...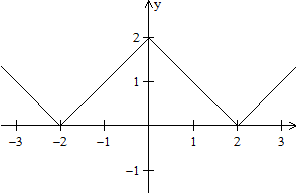 ... ... |
Es ergeben sich die vier Geradengleichungen mit
y=x-2, y=-x+2, y=-x-2 und y=x+2.
Sie gelten jeweils nur für die oben bestimmten Bereiche.
Dieses Beispiel entspricht der teilweise hochgeklappten
Parabel mit p(x) = |x²-1|.
|
Diskussion der Funktionsgleichung
y=|x+|x+1||
Auflösen der inneren Betragsstriche
Fall I
x+1>0 /\ y=|x+x+1|, vereinfacht x>-1 /\ y=|2x+1|
Fall II
x+1<0 /\ y=|x-x-1|, vereinfacht x<-1
/\ y=1
Auflösen der äußeren
Betragsstriche
Fall Ia
x>-1 /\ 2x+1>0 /\ y=2x+1, vereinfacht x>-1
/\ x>-1/2 /\ y=2x+1,
zusammengefasst x>-1/2 /\
y=2x+1
Fall Ib
x>-1 /\ 2x+1<0 /\ y=-2x-1, vereinfacht x>-1
/\ x<-1/2 /\ y=-2x-1,
zusammengefasst -1<x<-1/2
/\ y=-2x-1 |
Zusammenfassung im Graphen
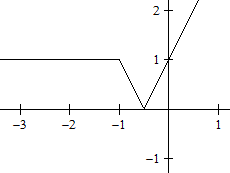
|
Relationen mit
Beträgen top
Verfremdung der Kreisgleichung
...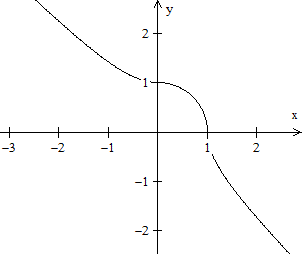 ... ... |
Der Einheitskreis ist der Graph der Relation x²+y²=1.
Man könnte Beträge in folgender Weise einführen:
|x|x+|y|y=1.
Der Graph links ist eher langweilig.
Der Kreis bleibt nur im 1. Quadranten erhalten.
Das ist verständlich, denn nur für x>0 und y>0
ist nach wie vor x²+y²=1. |
...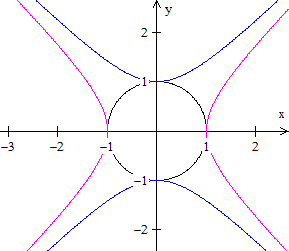 ... ... |
Betrachtet man die anderen Fälle, so liegt im 2.
Quadranten die (blaue) Hyperbel mit -x²+y²=1.
Im 4. Quadranten liegt die (rote) Hyperbel mit x²-y²=1.
Im 3. Quadranten gilt -x²-y²=1.
Die Gleichung wird von keiner Zahl erfüllt. Deshalb
bleibt das Feld leer. |
Quadrat
und Achteck
... ... ... |
... ... ... |
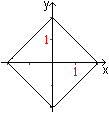
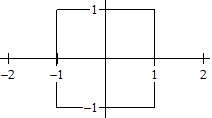
Es ist möglich, ein Quadrat
in einem Koordinatensystem nur durch eine Gleichung zu beschreiben,
|x|+|y|=2 oder abs(x)+abs(y)=2.
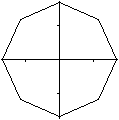
Es ist möglich, auch ein Achteck
in einem Koordinatensystem durch nur eine Gleichung zu beschreiben,
2(|x|+|y|)+sqrt(2)(|x-y|+|x+y|)=8. |
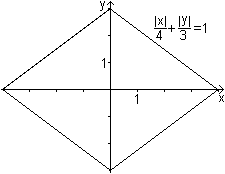
Aus dem Quadrat wird eine
Raute, wenn man die Gleichung von |x|+|y|=2 auf |x|/|a|+|y|/|b|=1 erweitert.
Oktaeder
...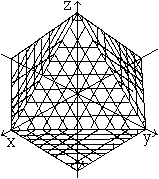 ... ... |
Es ist möglich, ein Oktaeder
in einem dreidimensionalen kartesischen Koordinatensystem durch eine Formel
darzustellen.
Die Formel lautet |x|+|y|+|z|=1 oder abs(x)+abs(y)+abs(z)=1. |
Vier
Quadrate
...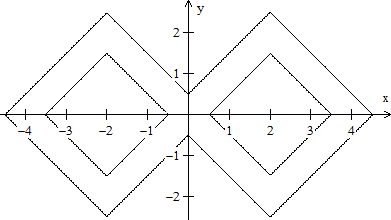 ... ... |
Auf der japanischen Webseite
http://www004.upp.so-net.ne.jp/s_honma/graph/absolutevalue.htm
fand ich die Gleichung |||x|-2|+|y|-2|=1/2 oder abs(abs(abs(x)-2)+abs(y)-2)=1/2
mit dem nebenstehenden Graphen. |
Noch
ein Quadrat
Für zwei beliebige reelle
Zahlen a und b ist der Term (1/2)(a+b+|a-b|) definiert.
Für a>b gilt (1/2)(a+b+|a-b|) = (1/2)(a+b+a-b)=a
Für a=b gilt (1/2)(a+b+|a-b|)=a
Für a<b gilt (1/2)(a+b+|a-b|) = (1/2)(a+b-a+b)=b
Der Term gibt also immer die größere Zahl an.
Man schreibt deshalb max(a,b)= (1/2)(a+b+|a-b|)
Der Term wurden früher
gerne in Computerprogrammen eingesetzt.
... ... ... |
Inzwischen kennen viele Programme in ihren Bibliotheken
den Ausdruck max(a,b), so auch das Programm WINPLOT, von dem ich
die Graphen auf dieser Seite habe zeichnen lassen.
Die Gleichung zum nebenstehenden Quadrat heißt
max(abs(x), abs(y))=1 oder max(|x|,|y|)=1. |
Für die kleinere Zahl
zweier Zahlen gilt die Gleichung min(a,b)=(1/2)(a+b-|a-b|).
Jetzt ist eine weitere Darstellung der Betragsfunktion
f(x) = |x| mit f(x) = max(x,-x) möglich.
Auch an anderen Stellen meiner
Homepage verwende ich Beträge.
Eilinien

y² = abs[sin(x)+0,1sin(2x)]
Betragsfunktionen
im Internet top
Deutsch
Hans-Joachim Vollrath [Mathematisch naturwissenschaftlicher
Unterricht 24(1971), 360-364]
Eine
Analyse der Betragsfunktion (.pdf-Datei)
Roland Fischer
Beispiele
für Betragsfunktionen
Wikipedia
Betragsfunktion,
Vorzeichenfunktion,
Norm
(Mathematik)
Englisch
Alexander Bogomolny (cut-the-knot)
Absolute
Value
Eric W. Weisstein (MathWorld)
Absolute
Value, Sign
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Absolute
value, Sign function,
Norm
(mathematics)
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2014 Jürgen Köller
top |

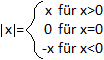 ...
...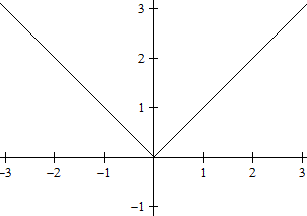 ....
.... ...
...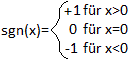

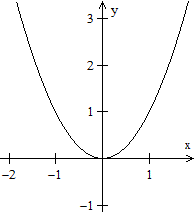
 ...
...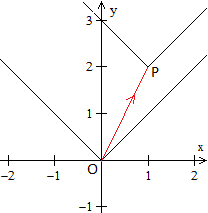 ...
...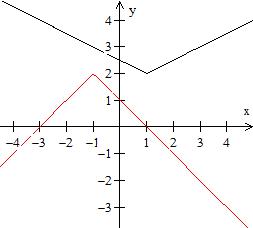
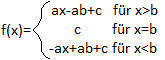 ...
...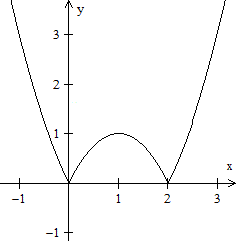

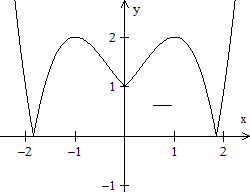
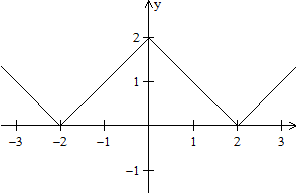 ...
...
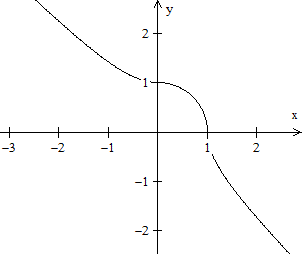 ...
... ...
... ...
... ...
... ...
... ...
... ...
...