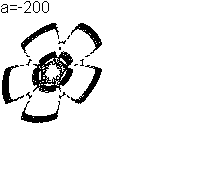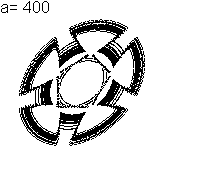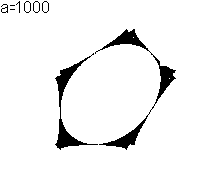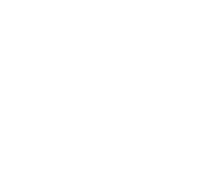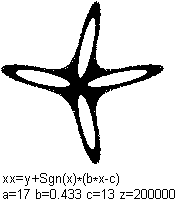|
Was ist Hüpfer?
Hüpfer ist eine Computergraphik, genauer ein Fraktal.
Bei Vorgabe eines Anfangspunktes werden mit Hilfe zweier
Formeln nacheinander die Koordinaten immer weiterer Punkte berechnet und
sofort gezeichnet. Die Punkte schließen sich zu Figuren zusammen.
Das Besondere ist und so kommt der Name Hüpfer zustande, dass die
Punkte um den Anfangspunkt herum in immer meist größeren Abständen
springen. Das konnte man in den achtziger Jahren, als diese Grafiken aufkamen,
bei den damals langsameren Computern gut erkennen. Heute sind die Bereiche,
in denen gerade gezeichnet wird, vergleichbar mit pulsierenden Ringen,
in die sich Kaskaden von Punkten ergießen.
Hüpfer ist die deutsche Bezeichnung von Hopalong
(hop-along, weiterhüpfen).
Der Erfinder von Hopalong ist Barry Martin von der Aston
University in Birmingham/England. A. K. Dewdney beschrieb diese Fraktale
im Magazin
Scientific American im September 1986 und machte sie
so bekannt. Die deutsche Ausgabe
Spektrum der Wissenschaft verbreitete
Hopalong in Deutschland in der Novemberausgabe 1986 mit einer Übersetzung
dieses Artikels in der Rubrik Computer-Kurzweil .
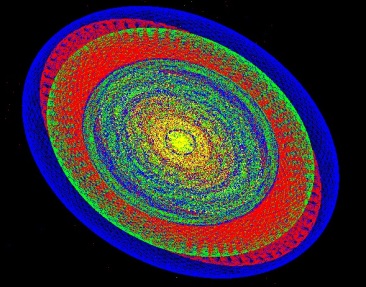
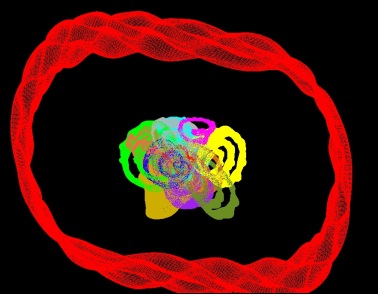
Es folgen drei typische Hüpfer-Bilder.
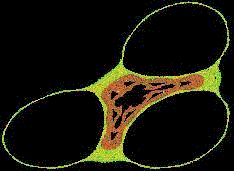
a=0.7, b=1, c=0
|

a=0.4, b=1, c=0
|

a=0.01, b= -0.3, c=0.003
|
Vor Jahren erstellt mit dem Programm "Winfract".
Algorithmus
top
In Dewdneys Aufsatz findet man das folgende Programm.
...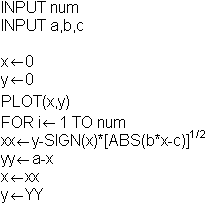 ... ... |
Erklärung:
Der Ausgangspunkt der Grafik ist der Punkt (x,y)=(0,0).
Nach zwei getrennten Formeln werden xx und yy berechnet.
Dabei tauschen sich x und y aus. Dann wird zum Plotten "umgeladen". Das
wiederholt sich bis num erreicht wird.
Die Variable i steht für einen Punkt, num ist die
Anzahl der Punkte.
Die Vorzeichenfunktion SIGN(x) ist gleich 1, wenn x>0,
-1 wenn x<0 ist; SIGN(0)=0.
ABS(x) ist die Betragsfunktion und ermöglicht ein
Wurzelziehen. |
Es gibt im Programm vier Variable, die eine Figur bestimmen.
Das sind die Parameter (a, b, c) und die Anzahl der Punkte num.
Wer sich mit Hüpfer beschäftigen will, sollte
- in welcher Programmiersprache auch immer - dieses einfache Programm ausprobieren.
Eigenes Programm
top
Wie viele Leser von Spektrum der Wissenschaft habe
ich damals dieses kleine Programm sofort ausprobiert. In den 90iger Jahren
benutzte ich dann ein Programm in Visual Basic 3, das ich hier nicht mehr
anbiete, da Programme in VB 3 unter Windows 7 nicht mehr funktionieren.
Hauptroutine des Programms:
Sub graph (u, v, a, b, c, z)
text9.Text = ""
x = 0: y = 0
For i = 0 To z
PSet (u + x, v + y)
xx = y + Sgn(x) * Abs(b
* x - c)
yy = a - x
x = xx
y = yy
If i / 10000 = Int(i /
10000) Then text9.Text = Str$(i)
Next i
text9.Text = "Ende"
End Sub................................................................................ |
Man erkennt das Programm von oben wieder.
>Der Einfachheit halber werden Bildschirmkoordinaten verwendet.
Dadurch ist die Einheit gleich einem Pixel.
>Die Variablen u und v legen fest, wo die Mitte einer
Figur liegt. Das kann in Visual Basic etwa (7000,5000) sein.
>Der erste Funktionsterm ist Sgn(x) * Abs(b * x - c).
Im Unterschied zum klassischen Hüpfer fehlt die Sqrt-Funktion.
So habe ich etwas Eigenes :-).
<text9.Text> ist sehr hilfreich. Man kann die Fortschritte
und das Ende des Zeichnens erkennen. |
Es folgen einige Bilder,
die ich mit meinem Programm huepfer.exe erstellte. Darunter stehen
jeweils die Parameter (a, b, c, num).

(500, 0.21, 100,150000)
|

(150, 0.22761, 100, 300000)
|

(300, 0.21, 50, 750000)
|

(366, 0.07, 50,1000000)
|

(500, 0.833, 120, 40000)
|

(150, 0.033, -80, 2000000)
|
Der Einfluss der Parameter auf ein
Bild ist voller Überraschungsmomente.
Eine Aussage kann man wagen: Je größer die
Parameter sind, desto größer wird die Figur. ;-)
Nur der Parameter oben links ändert sich.
Einige Tipps für das eigene Programmieren:
>Probiere alle möglichen Zahlen (auch negative Zahlen)
für a,b,c,num aus.
>Lasse die Funktion INT(x) weg. Es zeigt sich, wie wichtig
diese "Sprungfunktion" für einen Musterreichtum ist.
>Lasse die Funktionen SQR(x) und dann auch ABS(x) weg.
>Ersetze x durch 0.9999*x. Es ist erstaunlich,
dass trotz der Nähe zu 1 wegen der vielen Iterationen
die Grafiken klein bleiben.
>Ändere die Vorzeichen. Es wird deutlich, wie bestimmend
sie sind.
>Bringe Farbe in den Hüpfer.
>Verwende statt des Standardterms Sgn(x) * Sqrt((Abs(b
* x - c)) andere Terme so wie rechts. |
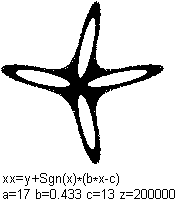 |
Wer kein eigenes Programm
schreiben will, findet zum Spielen in meiner Linksammlung unten ein Programm
von Ulrich Schwebinghaus/Henning Kopp (empfehlenswert!) und zwei Applets
von James Henstridge und Martin Junglas.
Dreidimensionale
Strukturen durch Selbstorganisation top
Wolfhard Hövel von der Georg-Simon-Ohm-Hochschule
Nürnberg fand diese Webseite und bot mir ein Applet an, mit dem man
Fraktale nach einem selbstentwickelten Algorithmus erzeugen kann. Er vermutete,
dass vielleicht einige Besucher Gefallen daran fänden. Vielleicht
stiegen einige Leser auf dieses Thema ein und stellten gar eigene Überlegungen
zur Diskussion.
Gerne stelle ich sein Programm, das Applet Attractor.jar,
hier vor.
Die Beschreibung findet man unter Selbstorganisation
von Vektoren in Form einer .pdf-Datei.
Kurzbeschreibung
Das Programm Attractor.jar erzeugt vielfältige Strukturen
im n-dimensionalen euklidischen Raum. Diese Attraktoren sind zum Teil instabil
und springen nach einer gewissen Lebensdauer in andere stabilere Formen
um. Für eine willkürlich vorgegebene Punktmenge im Raum wird
die Bewegung der Punkte derart geregelt, dass Schwerpunkt und Drehmoment
gleich bleiben. Die Vernetzung der Punkte erfolgt durch beliebig wählbare
Graphen. Zunächst betrachte man zwei Punkte (Ortsvektoren) im Raum.
Der eine Punkt wird iterativ um einen Einheitsvektor verschoben und der
andere ebenfalls um diesen Einheitsvektor, jedoch mit negativem Vorzeichen.
Damit bleibt der „Schwerpunkt“ dieses Punktpaars exakt erhalten. Diese
antiparallelen Verschiebungsvektoren liegen auf Parallelen, deren Abstand
ebenfalls konstant gehalten wird. Damit ist auch das „Drehmoment“ der beiden
Punkte konstant. Nun kann man weitere Punkte hinzufügen. Die Punkte
lassen sich frei wählbar zu Punktpaaren zusammenfassen. Es entsteht
also ein Graph, die Knoten des Graphen entsprechen den Punkten, die Kanten
den gewählten Punktpaaren. Laufen an einem Knoten mehrere Kanten zusammen,
werden die entsprechenden Verschiebungsvektoren für diesen Punkt vorzeichengerecht
addiert.
Für die verschiedensten Graphen und Dimensionen
können Attraktoren gefunden werden.
Beschreibung
der Benutzeroberfläche
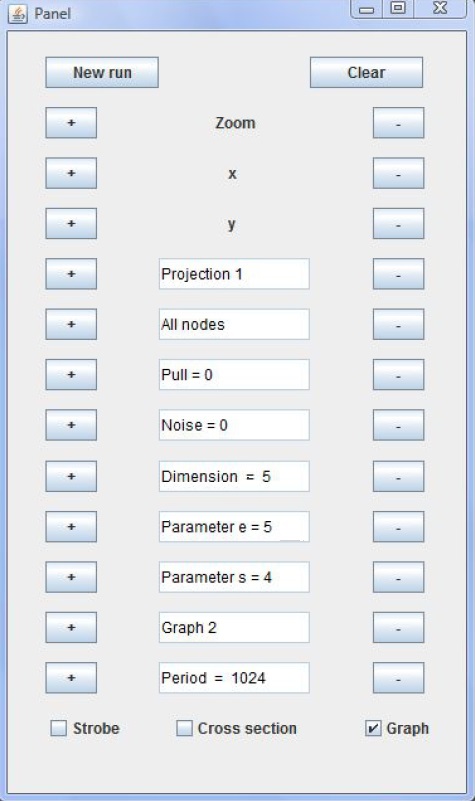
|
New run
Die Anfangsbedingungen werden zufällig neu gesetzt.
Clear
Der Bildschirminhalt wird gelöscht.
Zoom
Der Bildschirminhalt wird gelöscht und um den Faktor
1,2 vergrößert neu gezeichnet oder
entsprechend verkleinert.
x
Verschiebung des Bildes in x – Richtung.
y
Verschiebung des Bildes in y – Richtung.
Projection
Der Attraktor wird aus verschiedenen Richtungen auf den
Bildschirm projiziert. Die Anzahl der
Projektionen hängt von der gewählten Dimension
ab.
All nodes
Alle Knoten ( Ortsvektoren ) oder nur einzelne werden
gezeichnet. In diesem Beispielprogramm
sind maximal 12 Knoten möglich.
Pull
Die einzelnen Knotenpaare werden mit wachsender Intensität
auseinandergezogen. Dies erfolgt
durch einen Vektor, der in die 45° - Richtung wirkt.
Dabei können andersartige Attraktoren
entstehen.
Noise
Die Knoten werden mit wachsender Intensität zufällig
im Raum verschoben. Mit diesem
überlagerten Rauschen kann die Stabilität des
Attraktors geprüft werden.
Dimension
Die Dimension n des Raums kann ab n = 2 beliebig eingestellt
werden.
Parameter e
Der Parameter e beschränkt den maximalen Abstand
der Knoten eines Knotenpaars.
Parameter s
Der Parameter s bestimmt den Abstand der Parallelen,
auf denen die antiparallelen
Verschiebungsvektoren eines Punktpaars liegen.
Graph i
Hier kann man vorgegebene Graphen, für die Attraktoren
gefunden wurden, auswählen. Für
Graph i = 1 werden neue Graphen fortlaufend zufällig
erzeugt. Wird ein neuer Attraktor gefunden,
stoppt die Suche automatisch.
Period = i
Es werden i Iterationen durchgeführt und dann die
berechneten Pixel gezeichnet.
Strobe
Der Bildschirm wird vor jeder Periode gelöscht.
Mit Period und Strobe kann das dynamische
Verhalten der Attraktoren untersucht werden.
Cross section
Aus der Struktur wird eine dünne Scheibe herausgeschnitten
und gezeichnet. Die Anzahl der
möglichen Darstellungen hängt von der gewählten
Dimension ab.
Graph
Der verwendete Graph, der die Kopplung der Knoten ( Ortsvektoren
) bestimmt, wird angezeigt. |
Zwei Graphen
Hinzugefügt werden noch
zwei Links, die mir Wolfhard Hövel für weitere Studien mitgeteilt
hat.
Dreidimensionale
Strukturen durch Selbstorganisation und Strukturen
im n-dimensionalen Raum.
Verwandte
Webseiten meiner Homepage top
Hüpfer im Internet
top
Deutsch
Ulrich Schwebinghaus
(fraktalwelt)
Iterationen
II - Hopalong (mit Programm zum Herunterladen)
Englisch
flickriver
Photos
tagged with hopalongattractor
James Henstridge
Hopalong
Orbit Fractal (Applet)
Martin Junglas (fluxury)
Hopalong
Fractals (Applet)
Paul Bourke
Fractals
and Computer Graphics
Wolfram Demonstrations Project
Orbits
of the Hopalong Map
Referenzen top
A.K.Dewdney: Computer-Kurzweil, Spektrum der Wissenschaft,
November 1986
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2003, überarbeitet 2014, Jürgen Köller
top |



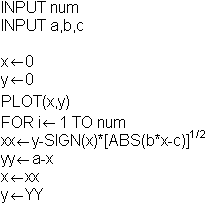 ...
...