Tetraflexagon
Inhalt dieser Seite
Was ist ein Tetraflexagon?
Zwei Tri-Tetraflexagone
Drei Tetra-Tetraflexagone
Zyklisches Hexa-Tetraflexagon		 Weitere Tetraflexagone
Tetraflexagon mit der Röhrentechnik
Tetraflexagone im Internet
Referenzen.
Zur Hauptseite    "Mathematische Basteleien"

Was ist ein Tetraflexagon?
...... Ein Tetraflexagon ist ein 2x2-Quadrat, das man aus einem Streifen Papier faltet. 

Das Besondere ist, dass man das Flexagon auf der Rückseite wie ein Buch öffnen kann. Dann erscheint ein weiteres 2x2-Quadrat, das vorher verborgen war. 

Im einfachsten Fall hat das Flexagon drei Oberflächen. Das ist dann ein Tri-Tetraflexagon, also 3-4-Flexagon.
Weiterhin gibt es das Tetra-, Penta-, Hexa-Tetraflexagon usw. mit 4, 5, 6, ....Oberflächen.

Zwei Tri-Tetraflexagone top
Bau
1
...... Zeichne die nebenstehende Figur aus sieben Quadraten auf normales, kariertes Schreibpapier und schneide sie aus. Wähle als Seitenlänge eines Quadrats zum Beispiel a=2 cm. 
Zur Verdeutlichung wird auf dieser Seite die Vorderseite grün, die Rückseite blau gefärbt. 

2
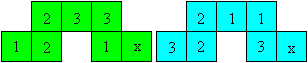...... Beschrifte die Vorder- und Rückseite der Quadrate mit 1, 2 und 3. 
Zwei Quadrate erhalten ein x. Sie werden später aufeinandergeklebt. 
3
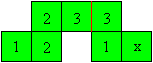
Falte den Streifen an der roten Linie, so dass die Quadrate mit den Dreien aufeinander liegen. 
4
......
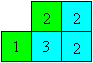
 Schiebe das Quadrat mit der 3 unter das grüne Quadrat 2, so dass auf der Rückseite zwei Dreien aufeinanderliegen.
5
......
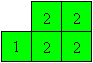 Klebe auf der Rückseite die x-Felder aufeinander. 
6
Das Tri-Tetraflexagon ist fertig. Die Vorderseite trägt eine 2, die Rückseite 1, verborgen ist 3.
Öffnen der dritten Oberfläche
1 Drehe das Flexagon so, dass die Oberfläche 2 oben liegt. 
2 Falte das Flexagon nach unten. Hinter B liegt ein Berg.
3 Lege die Kanten hinter A und A aufeinander. 
4 Öffne das Flexagon oben bei B wie ein Buch.
5 Breite das Flexagon flach aus. Die Oberfläche 3 ist oben. 
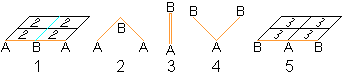
Diesen Vorgang kann man durch ein Diagramm festhalten: 
Vor dem Strich stehen die beiden Ausgangsflächen 12. Die Oberfläche 2 kann geöffnet werden, denn die Zahl 2 steht auch rechts des Striches. Die Oberfläche mit der anderen Zahl (3) ist nach dem Öffnen sichtbar. 
Es ist möglich den Vorgang des Öffnens rückgängig zu machen und so wieder zu den Oberflächen 1 und 2 zu gelangen. 
Wieder kann man 2 öffnen und dann erscheint die Oberfläche 1. 
Beschreibung
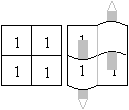
Das Flexagon zeigt vier Quadrate, wird aber aus sechs quadratischen Blättchen hergestellt. Das Quadrat mit x zählt nicht. 
Es liegen entweder zwei Blätter übereinander oder zwei Blätter einzeln. Ganz gleich, welche Zahl oben steht, die Einzelschichten liegen immer in Richtung der Nebendiagonalen(\), zwei Schichten in Richtung der Hauptdiagonalen (/). 
...... Die Oberfläche 1 (und 3) haben zwei Ösen, in die hier zur Verdeutlichung ein Bleistift hineingesteckt wird. 

Das sind auch die Oberflächen, die man nicht weiter öffnen kann und die dann "Sackgassen" sind. 

...... Die Oberfläche 2 hat zwei Zipfel, die in Richtung der Nebendiagonale liegen. 
Das sind Quadrate, die zur Mitte nach zwei Seiten hin frei sind. 
Das ist die Oberfläche, die man öffnen kann.

Es wird sich zeigen, dass die "höheren" Flexagone eine ähnliche Struktur haben. Es gibt jeweils zwei Arten der Oberfläche.
Spiegelbild
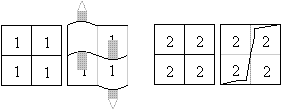...... Das Flexagon ist punktsymmetrisch.

Spiegelt man das obige Tri-Tetraflexagon an der vertikal liegenden Mittellinie, so entsteht ein neues, spiegelbildliches Flexagon.
Man kann es leicht bauen. 
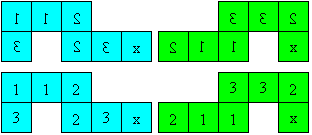...... Spiegelt man die Vorlage von oben, so erhält man eine Vorlage für das spiegelbildliche Flexagon. 
Das Spiegelbild hat die gleiche Struktur und bietet nichts Neues. Deshalb unterscheidet man nicht zwischen den beiden Formen. 

Drei Tetra-Tetraflexagone top
Bau des linearen Tetra-Tetraflexagons 
1
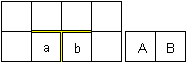
Zeichne zwei Rechtecke 4x2 und 2x1 und schneide sie aus.
Schneide das große Rechteck längs der gelben Linien ein. 
Klebe das Quadrat B auf b. Dann liegt Quadrat A frei über a.

2
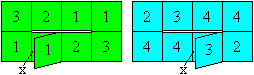
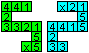
Beschrifte das Flexagon vorne und hinten wie angegeben. 
3
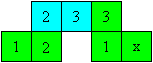
Falte den Streifen so, dass die Quadrate mit den Vieren aufeinander liegen. 

Es entsteht die Grundfigur des Tri-Tetraflexagons. Lege dann wieder 3 auf 3 und klebe x auf x.

Öffnen
...... Man öffnet das Flexagon genau so wie das Tri-Tetraflexagon. 
Dieser Vorgang wird durch das nebenstehende Diagramm dargestellt.
Bau des Tetra-Tetraflexagons mit 2 Sackgassen
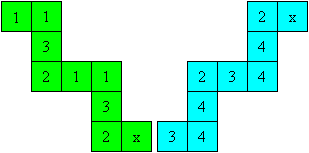
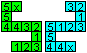
Stelle eine Vorlage wie links angegeben her.

Lege 2x die Quadrate 4 auf 4 aufeinander.
Lege 2x 3 auf 3.
Schiebe das Quadrat x unter ein Quadrat.
Dann liegt x auf x und eine weitere 1 oben. 
Klebe die Quadrate mit x aufeinander. 

 
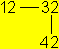...... Das Besondere an diesem Flexagon ist, dass man nur zu Quadrat 4 gelangt, wenn man von 32 aus das Quadrat 2 horizontal öffnet. Das wird im Diagramm veranschaulicht, indem man 42 unter 32 schreibt.
Bau des zyklischen Tetra-Tetraflexagons
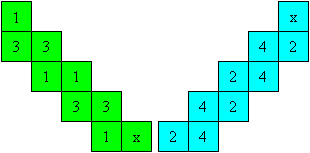
Stelle eine Vorlage wie links angegeben her.

Lege 2x die Quadrate 4 auf 4.
Lege 2x die Quadrate 3 auf 3.
Schiebe das Quadrat x unter ein Quadrat.
Dann liegt x auf x und eine weitere 2 liegt oben. 
Klebe die Quadrate mit x aufeinander. 
......
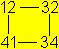 Das Besondere an diesem Flexagon ist, dass man es zyklisch öffnen kann.

Zyklisches Hexa-Tetraflexagon top
Bau
1
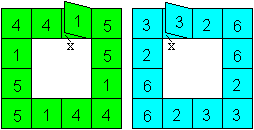
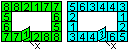
Stelle eine Vorlage wie links angegeben her.

Lege 2x die Quadrate 6 auf 6.
Lege 2x die Quadrate 5 auf 5.

2
Lege 2x 4 auf 4 und einmal 3 auf 3. 
3
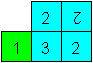...... Schiebe das Quadrat mit der 3 unter das grüne Quadrat, so dass auf der Rückseite zwei Dreien aufeinanderliegen. 
Falte die 1 nach hinten und klebe die x-Quadrate aufeinander. Das Flexagon ist fertig. 
Beschreibung
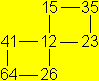...... Öffnet man das Flexagon systematisch, so erhält man das nebenstehende Diagramm. 
Es hat die Form zweier Quadrate, die einen Eckpunkt gemeinsam haben. 

Es werden zwei Zyklen mit der Nahtstelle 12 durchlaufen.

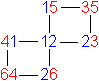...... Im Diagramm kommen die Quadrate 1 und 2 3x vor und bilden zusammen ein Kreuz.
Die Quadrate 3, 4, 5 und 6 kommen 2x vor und bilden die freien Seiten des Doppelquadrats.
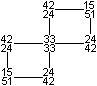...... Das Flexagon besteht aus 12 Blättern, die sich auf vier Quadrate verteilen. Es gibt für jedes Quadrat 1, 2, 3 oder 4 Schichten, zwei nebeneinanderliegende Quadrate haben die Verteilung 15, 24 und 33. 
Bestimmt man für jeden Zustand des Flexagons die Anzahl der Blätter, so ergibt sich die nebenstehende Verteilung.
Man kann das zyklische Tetra-Tetraflexagon auch ohne zu kleben herstellen. Anleitungenen findet man bei Arvind Gupta (URL unten).

Weitere Tetraflexagone top
Man faltet die folgenden Flexagone, indem man Quadrate gleicher Nummerierung aufeinanderlegt. Man beginnt immer mit der größten Zahl und legt dann in absteigender Reihenfolge die Quadrate aufeinander. 
Penta-Tetraflexagon mit 2 Sackgassen
Zyklisches Penta-Tetraflexagon mit 1 Sackgasse

Hexa-Tetraflexagon mit 2 Sackgassen 
Septa-Tetraflexagon mit 2 Sackgassen
Okta-Tetraflexagon mit 2 Sackgassen
Man findet weitere Tetraflexagone, wenn man zwei Paare von Quadraten mit gleicher Nummerierung aufeinander klebt. 

Tetraflexagon mit der Röhrentechnik      top
Bau
1
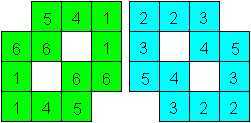
Stelle eine Vorlage wie links angegeben her.
Schneide auch die beiden Quadrate innen aus. 

2
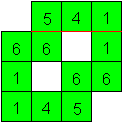
Falte an der roten Linie. Dort entsteht ein Tal.
3
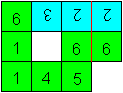
Falte an der roten Linie.

4
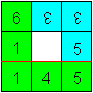
Falte an der roten Linie.

5
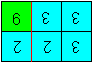
Falte an der roten Linie.
Stecke das Quadrat oben links unter die daneben liegende 3.
6
Das Tetraflexagon ist fertig. 
Öffnen
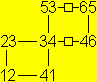...... Die Quadrate 1 bis Fünf findet man durch normales Öffnen des Flexagons. Die Wege zwischen 53 und 65  sowie zwischen 34 und 46 erfordern eine neue Technik, die bei David Mitchel "Tube Flex" ("Röhrenfaltung") heißt. 
Tube Flex


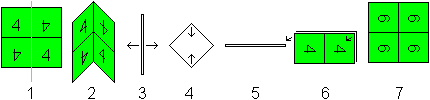
1 Betrachte Oberfläche 4. Auf der Rückseite liegt 3.
2 Falte das Flexagon an der blauen Linien, einem Berg. 
3 Öffne das Flexagon zu einer Röhre.
4 Lege die untere und obere Ecke aufeinander.		 5 Breite das Papier flach aus. 
6 Drehe das Flexagon in die Vertikale.
7 Öffne es so, dass die Oberfläche 6 oben liegt. 
.

Vorlagen für diese Flexagons findet man im Heftchen von David Mitchell (s.u.) oder auf der Seite von Harold V. McIntosh (URL unten).
Auf meiner Homepage gibt es weitere Seiten über Flexagone: Flexagon, Hexahexaflexagon, Flexatube.
Kaleidozyklen könnte man als dreidimensionale Flexagone ansehen. 

Tetraflexagon im Internet    top

Deutsch

Claus Michael Ringel 
Flexagone

Englisch

Dave Root (Cool Science Tricks)
Flexagons

Eric W. Weisstein
Tetraflexagon
 
Flexagon Funhouse
HOW TO MAKE A FLEXAGON
How to make a  2x3 Tetraflexagon

Harold V. McIntosh 
Tetragonal Flexagons

Jill Britton
TETRA-TETRA-FLEXAGON

Wikipedia
Flexagon
 

Videos

YouTube
http://de.youtube.com/watch?v=Ti0vOfucHnU

Referenzen     top
(1) Martin Gardner: The Second Scientific American Book of Mathematical Puzzles & Diversions, New York 1961
(2) Martin Gardner: Mathematische Denkspiele, München 1987 (ISBN 3 88034 323 3) 
(3) David Mitchell: The Magic of Flexagons, Norfolk England 1998 (ISBN 1 899618287) 
(4) Jill Russell: A Family of Tetraflexagons (http://www.sherston.freeserve.co.uk/HTML/Mathematics/JillsFlexagons.htm)

 Feedback: Emailadresse auf meiner Hauptseite

Diese Seite ist auch in Englisch vorhanden.

URL meiner Homepage:
http://www.mathematische-basteleien.de/

© 2006 Jürgen Köller

top
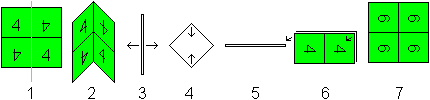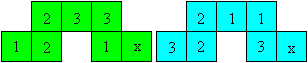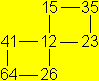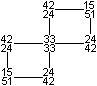
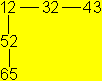
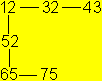
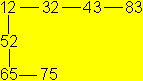
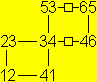