|
Was ist ein Flexatube?
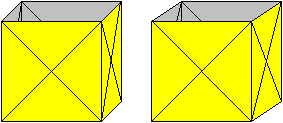
3D-Bild
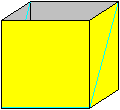
Ein Flexatube ist eine Puzzle aus Papier.
Es besteht im einfachsten Falle aus vier Quadraten, die zu einem oben und
unten offenen Würfel zusammengefügt sind. Die vier Kanten und
die Flächendiagonalen sind Faltlinien.
Es stellt sich folgende Aufgabe:
>Krempele das Flexatube allein durch Falten um.
>Anders ausgedrückt, kehre das Innere nach außen und das
Äußere nach innen.
Das also ist das Ziel:
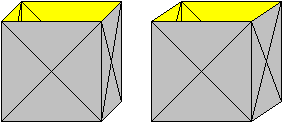
Dagegen ist einen Strumpf umzukrempeln eine leichte Übung ;-).
Die Farben Gelb und Grau in den Zeichnungen auf dieser Seite sollen
die Beschreibungen unterstützen.
Flexatube heißt wörtlich übersetzt
Faltrohr. Ich belasse es beim englischen Namen.
In Mitchells Heft (1) heißt es Flexitube. Man findet auch Flexotube.
Das Flexatube ist ein Klassiker unter den Faltpuzzles und zählt
zu den Flexagons oder ist verwandt mit ihnen. Sie wurden in der einfachen
Form von Arthur H. Stone in den 1930iger Jahren entdeckt. Populär
wurden sie durch die Veröffentlichungen von Martin Gardner.
Flexagons findet man in Gardners erstem Buch ("Mathematical Puzzles
& Diversions"), Flexatubes im zweiten ("The Second Scientific American
Book of Mathematical Puzzles and Diversions"). Die beiden Bücher wurden
zur Übersetzung ins Deutsche zu einem Buch ("Mathematische Rätsel
und Probleme") zusammengefasst. Offenbar war der damals verantwortliche
Redakteur kein großer Freund von Faltarbeiten. Neben dem Kapitel
über Flexagons ließ er auch das Kapitel über Tetraflexagons
weg.
Es gibt zahlreiche Variationen und Weiterentwicklungen des Flexatubes.
Einige findet man bei (1).
Bau des Flexatubes top
Der Bau ist einfach.
>Gib ein weißes DINA4-Blatt vor.
... ... |
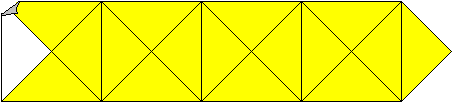>Zeichne ein Streifen aus vier Quadraten mit der Seitenlänge 5cm
mit ihren Diagonalen wie links.
>Füge rechts ein Viertelquadrat hinzu.
>Schneide den Streifen aus.
>Ziehe die Linien mit einem leeren Kugelschreiber nach und falte die
Linien vor. |
>Klebe das überstehende Viertelquadrat rechts auf das weiße
Feld links und bilde so einen außen gelben Ring.
>Forme den Würfel.
Lösung top
Erste Phase
1
2
|
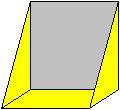
Das sieht dann so aus.
 |
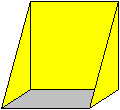
3
|
Drehe das Papier so, dass das graue Quadrat horizontal liegt.
|
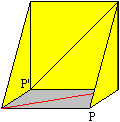
4
|
Falte an den beiden roten Linien. Sie sind Täler.
Dabei legt man Punkt P auf Punkt P'.
|
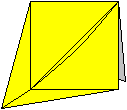
5
|
Das sieht dann so aus.
|
6
... ... |
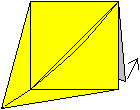Es entsteht hinten ein halbes Quadrat. Drehe es nach hinten bis es
etwa senkrecht auf dem gelben Quadrat steht.
|
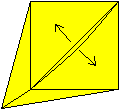
7
|
In der Mitte ist ein Schlitz entstanden. Erweitere ihn in Pfeilrichtung.
|
8
... ... |
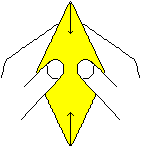Die ist eine Zeichnung meiner Seite Papierschiffchen.
Wie dort muss man den Schlitz erweitern und schließlich die beiden
Spitzen oben und unten aufeinanderlegen.
|
9
|
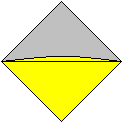
Das sieht dann so aus. Oben hat sich eine Tasche gebildet.
|
Zweite Phase:
10
|
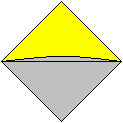
Drehe das Papier um.
Auf der Rückseite ist wieder die Tasche, doch sind die Farben ausgetauscht.
|
Von jetzt an kehrt man alle Schritte und
ihren Ablauf um.
11
... ... |
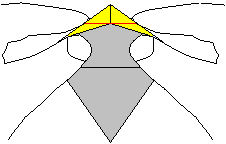Greife mit beiden Daumen in die Tasche und drücke mit den Zeigefingern
die seitlichen Quadrate an den roten Linien ein. |
12
 |
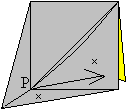Das sieht dann so aus.
Ziehe die beiden angekreuzten Stücke hoch und damit auch die Ecke
P hoch.
|
13
 |
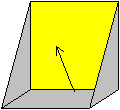Das sieht dann so aus.
Ziehe die horizontal liegende graue Fläche hoch.
|
14
 |
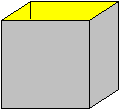Am Ende steht das gelöste Flexatube.
|
Eine zweite Lösung top
......
Schritt 9
|
Es gibt eine einfache Lösung in Heft (1).
Die zweite Phase
(oben Schritt 10 bis 14) ist hier leicht zu
verstehen:
Man steckt den gelben Zipfel unten in die graue Tasche oben und entfaltet
das Papier wieder.
Erste Phase:
Die Schritte 1 bis 9 ergeben sich, wenn man dieses Hineinstecken und
Entfalten umkehrt.
Das ist knifflig. |
Flexatubes im Internet top
Englisch
Serhiy Grabarchuk (Age of Puzzles)
Arthur
Stone's Flexatube
Eric W. Weisstein
Flexatube
Harold V. McIntosh
General
Tetraflexagon, Flexatube, or Bregdoid
Kommentar top
Das Flexatube hat Eigenschaften eines guten Puzzles.
>Es ist einfach aufgebaut und leicht herzustellen.
>Es ist jedem möglich nach etlichen Minuten eine Lösung zu
finden. Man weiß nicht, wie man zu der Lösung gekommen ist.
>Will man den Lösungsweg wiederholen, ist man gezwungen nach einem
Plan vorzugehen.
>Es gibt mehrere voneinander unabhängige Lösungen.
>Die Lösungen verwenden die Umkehrbarkeit von Faltungen. Das führt
dazu, dass eine Lösung zwei Teile hat.
Referenzen top
(1) David Mitchell: The Magic of Flexagons, Norfolk England 1998 (ISBN
1 899618287)
(2) Martin Gardner: The Second Scientific American Book of Mathematical
Puzzles and Diversions, Simon & Schuster (1961)
(3) Martin Gardner: Wheels, Life, and other Mathematical Amusements,
Freeman (1983) New York
(3') Martin Gardner: Mathematische Denkspiele, Hugendubel München
1987 (ISBN 3 88034 323 3)
(Die Kombinatorik des Papierfaltens,
Seite 32ff.)
Feedback: Emailadresse auf
meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2005 Jürgen Köller
top |
