|
Was ist Taxi-Geometrie?
... ... |
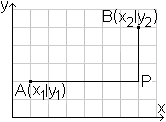Die Taxi-Geometrie ist eine Form der Geometrie, in der der Abstand
zweier Punkte A und B nicht als Länge der Strecke AB definiert wird,
sondern als Summe der Beträge der Differenzen ihrer Koordinaten.
Formel: AP+PB= |x2-x1| + |y2-y1|
Dabei haben die Punkte in der einfachen Version nur ganzzahlige Koordinaten,
und ihre Verbindungen sind Gitterlinien. |
... ... |
Hinter dem Namen steht folgender Sachverhalt.
Man kann das Gitter als ein Netz von Straßen auffassen, das ein
Taxifahrer durchfährt.
Die Kreuzungen bilden die Orte, die er anfahren kann.
Es ist bemerkenswert, dass der Taxifahrer unterschiedliche Wege - von
A ausgehend - nehmen kann, die die gleiche Weglänge haben, vorausgesetzt,
er nähert sich stetig dem Ziel B. |
Fährt der Taxifahrer nur geradeaus, so gibt es keinen Unterschied
zwischen Taxi- und euklidischer Geometrie.
Neben der Bezeichnung Taxi-Geometrie findet man
auch die Namen City-Block-, Manhattan- oder Minkowski-Geometrie.
Auf Hermann Minkowski (1864 bis 1909) geht die Idee zurück.
Grundlage dieser Webseite ist ein Kapitel
in Gardners Buch (1).
T-Strecke top
In der euklidischen Geometrie gibt es zu zwei Punkten genau eine Strecke
mit wohldefiniertem Abstand, in der Taxi-Geometrie zu einem Abstand mehrere
Strecken.
... ... |
Das deutet noch einmal die Zeichnung an. Beide Strecken haben die Länge
9.
Zur Kennzeichnung dieser neuen Art von Strecke nennt man sie auch Taxi-Strecke
oder T-Strecke. |
... ... |
... ... |
Es stellt sich die Frage, wie viele T-Strecken es zwischen zwei Punkten
gibt.
In diesem einfachen Fall kann man die Wege abzählen und kommt auf
die Anzahl 6. |
... ... |
Bei einer systematischen Untersuchung entdeckt man eine Gesetzmäßigkeit.
Die Anzahl der Wege an einer Kreuzung ist immer die Summe der Wege an
den vorhergehenden Kreuzungen.
Das führt zum pascalschen Dreieck, dessen Zeilen hier als Diagonalen
auftreten. |
.. .... |
... ... |
Der Punkt B liegt von A aus gesehen auf der neunten Diagonale und somit
auch in der neunten Zeile des pascalschen Dreiecks, und zwar an der vierten
Stelle.
Da liegt die Zahl 28+56=84 oder "9 über 3".
Es gibt also 84 Wege, um für den Fall "6 nach rechts, 3
hoch" von A zu B zu gelangen.
Allgemein ist für "n nach rechts, m hoch" die Anzahl "n+m über
m". |
T-Linie
... ... |
Der Vollständigkeit halber sei auch eine beliebige T-Verbindungslinie
zwischen A und B gezeichnet, die keine T-Strecke ist.
Sie besteht aus den T-Strecken AC, CD, DE und EB. |
T-Vieleck top
Vielecke müssen auch neu gesehen werden.
... ... |
In der nebenstehenden Figur werden die Punkte A und B durch zwei T-Strecken
der Länge 8 verbunden.
Es entsteht ein Zweieck AB, das es in der euklidischen Geometrie nicht
gibt. |
Gibt man einen dritten Punkt C vor, so ist es eine Sache der Definition,
ob die Punkte A, B und C ein T-Dreieck bilden.
>Dafür spricht, dass sie in der euklidischen Geometrie ein Dreieck
bilden.
>Dagegen spricht, dass A, B und C auf einer T-Strecke liegen.
Ich folge auf dieser Seite Martin Gardner (1), der T-Dreiecke dieser
Art zulässt, und das ist auch üblich.
In diesem Sinne steckt in der Figur auch
das Viereck ADBC der Seitenlänge 4.
Konsequenterweise ist die Figur auch ein
T-16-Eck der Seitenlänge 1, auch wenn sich das merkwürdig anhört.
T-Quadrat?
| ...... |
Man könnte einen Schritt weitergehen und das Viereck ADBC
als T-Raute bezeichnen, da vier Seiten gleich lang sind. Es ist kein T-Quadrat,
da der Winkel bei D ein gestreckter ist.
Problematisch an dieser Definition ist, dass viele Eigenschaften der
Raute verloren gehen, z.B. die Symmetrie. |
In der euklidischen Geometrie ist ein Viereck ein
Quadrat, wenn die Seiten gleich lang sind und die Winkel rechte Winkel.
... ... |
In diesem Sinne sind die nebenstehenden Vierecke T-Quadrate.
Verbindet man die Punkte durch gerade Linien, ergibt sich eine Raute.
Ist es also eine Raute und kein Quadrat? |
... ... |
Will man alle Eigenschaften des Quadrats fordern, sollte man nur das
Quadrat der euklidischen Geometrie als T-Quadrat zulassen. |
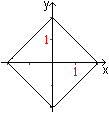
Einen anderen Zugang zum Quadrat liefert
die Relation mit |x|+|y|=2 und D=|R.
Sie lässt sich leicht auf die Taxi-Geometrie übertragen.
Es wird sich herausstellen, dass dieses
Quadrat auch als Kreis angesehen werden kann, merkwürdig.
T-Gerade top
... ... |
Man erhält aus der T-Strecke eine T-Gerade, indem man die T-Strecke
über beide Endpunkte hinaus verlängert.
Dabei ist hier darauf zu achten, dass es immer "aufwärts" geht. |
... ... |
Untersucht man zwei Geraden auf Schnittpunkte, so kann man jede Anzahl
an Schnittpunkten erreichen.
Hier schneiden sich die Geraden in zwei Punkten. Ändert man die
steigende (schwarze) Gerade so ab, dass sie ab S1 auch horizontal
verläuft, so ist die Anzahl der Schnittpunkte beliebig groß. |
Wegen der Vielfalt möglicher Geraden lohnt es sich nicht, sie noch
weiter zu untersuchen.
Interessanter sind der T-Kreis und die T-Ellipse in den nächsten
Abschnitten.
T-Kreis top
Ein Kreis
... ... |
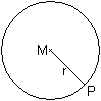Gibt man einen festen Punkt M vor und markiert alle Punkte, die den
Abstand r vom Mittelpunkt M haben, erhält man einen Kreis. |
Diese Aussage überträgt man auf
die Taxi-Geometrie.
... ... |
Gibt man einen festen Punkt vor und markiert alle Punkte, die den T-Abstand
3 haben, erhält man 12 Punkte. Sie bilden ein auf der Spitze stehendes
Quadrat der T-Seitenlänge 6.
Verallgemeinerung:
Gibt man einen festen Punkt vor und markiert alle Punkte, die den T-Abstand
r haben, erhält man 4r Punkte. Sie bilden ein auf der Spitze stehendes
Quadrat der T-Seitenlänge 2r. |
Dieser Sachverhalt erinnert an die Quadratur
des Kreises, bei der der Kreis in ein flächengleiches Quadrat übergehen
soll.
Die Mittelpunktsgleichung eines Kreises
ist im kartesischen Koordinatensystem x²+y²=r². Hier gilt
|x|+|y|=r.
Zwei Kreise
... ... |
Wie bei den gewöhnlichen Kreisen schneiden sich zwei T-Kreise
in keinem, in einem oder in zwei Punkten. |
Bei T-Kreisen gibt es noch weitere Fälle.
... ... |
Zwei T-Kreise mit den T-Radien R und r schneiden sich in mehr als zwei
Punkten, z.B. in drei.
Die Anzahl n der gemeinsamen Punkte wird in dieser Ecklage durch den
kleineren T-Radius bestimmt.
Es gilt n=2r+1 für r<R. |
... |
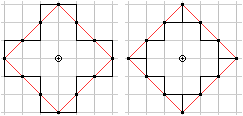Vielleicht sollte man die Punkte des T-Kreises nicht miteinander verbinden.
Der Eindruck vom Quadrat geht verloren. |
T-Ellipse top
Horizontal-Lage
... ... |
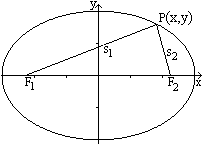Ein Ellipse besteht aus allen Punkten, deren
Summe der Abstände von zwei festen Punkten F1 und F2
gleich ist.
Die Summe ist in der Zeichnung s=s1+s2.
Die beiden festen Punkte F1 und F2 heißen
Brennpunkte. |
Wie bei der Ellipse wird eine T-Ellipse
durch den Abstand der Brennpunkte b und die konstante Summe s bestimmt.
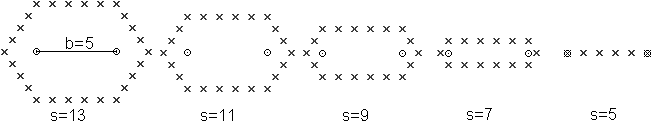
Ein einfaches Computerprogramm findet heraus, dass Figuren aus zwei
Trapezen mit einer gemeinsamen Grundlinie entstehen. Die freien Grundlinien
sind genau so lang wie die Strecke b=F1F2
.
Im Falle s=b=6 entsteht eine Zeile, in deren Eckpunkte die Brennpunkte
liegen.
|
hier:
b=2, s=6 |
Der Computer zeichnet nur T-Ellipsen, wenn entweder
> b und s gerade sind wie in der nebenstehenden Zeichnung oder
> b und s ungerade sind wie in den Computerbildern oben. |
Erklärung: Für den linken Scheitelpunkt
der T-Ellipse z.B. gilt s=2x+b oder s-b=2x oder "s-b ist eine gerade Zahl".
Daraus folgt, dass s und b gleichzeitig gerade oder gleichzeitig ungerade
sind.
Schräg-Lage
Andere Figuren entstehen, wenn die Brennpunkte diagonal liegen.
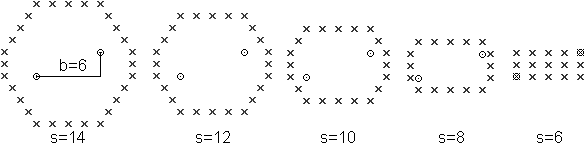
Ein einfaches Computerprogramm findet heraus, dass es bei einem konstanten
T-Abstand Figuren gibt, denen ein Rechteck 3x5 zugrunde liegt. Im Falle
s=b entsteht ein ausgefülltes Rechteck, dessen Eckpunkte auch Brennpunkte
sind.
Zustandekommen einer T-Ellipse mit b=6
und s=10
1 Der Punkt oben rechts liegt auf einer T-Strecke durch die Brennpunkte.
Es gilt (2+6)+2=10.
2 Über andere T-Strecken findet man fünf weitere Punkte.
Für einen Punkt ist die T-Strecke eingezeichnet.
3 Aus Symmetriegründen ergeben sich sechs weitere Punkte auf den
schrägen Linien.
4 Zum Punkt oben rechts gibt es links daneben vier weitere Punkte.
Der Abstand zum rechten Brennpunkt wird schrittweise um 1 größer,
zum linken um 1 kleiner, bis man zu einem Punkt über dem linken Brennpunkt
gelangt. So bleibt es bei der Summe 10. - Die gleichen Überlegungen
gelten für die fünf Punkte unten.
5 Die Überlegungen zu 4 kann man auf die vertikal liegenden Punkte
übertragen. Das sind zwei weitere Punkte, rechts und links.
Diese Überlegungen kann man auf beliebige T-Ellipsen verallgemeinern.
... ...
|
Es stellt sich also heraus, dass die Anzahl der waagerecht und
senkrecht liegenden Punkte durch die Anzahl der Punkte im Steigungsdreieck
bestimmt sind. Das sind die Zahlen 5 und 3.
Oben liegen die Brennpunkte nebeneinander. Die Zahlen heißen da
1 und 5 bzw. 1 und 3. |
Ergänzung
... ... |
Oben erkannte ein Computerprogramm, dass ein gefülltes Rechteck
3x5 auch eine T-Ellipse ist. Es gilt b=s=6.
Legt man die Brennpunkte diagonal außerhalb des Rechtecks in
die Mitte eines Gitterquadrats wie links, so ergibt sich das gleiche Rechteck.
Es gilt b=s=8. |
Ausblick top
>In Gardners Buch (1) findet man noch Untersuchungen der T-Hyperbel
und der T-Parabel, die auch über Abstandsbedingungen erfasst werden.
>Statt des quadratischen Musters könnte man auch ein Dreiecksmuster
vorgeben.
>Eine Verallgemeinerung der Taxi-Geometrie besteht darin, den T-Abstand
nicht nur über ganze, sondern auch über reelle Zahlen zu definieren.
Das wird auf der Seite Taxicab geometry von en.wikipedia erwähnt.
(Unter dieser Sicht verschwinden einige Widersprüche auf dieser
Seite, z.B. bei der Raute und beim Quadrat.)
>Auch in anderer Hinsicht kann verallgemeinert werden. Statt des ebenen
Gitters gibt man ein Raumgitter oder gar ein Gitter in einem höherdimensionalen
Raum vor und betreibt dort Taxi-Geometrie.
Taxi-Geometrie
im Internet top
Deutsch
Wikipedia
Manhattan-Metrik,
Französische
Eisenbahnmetrik, Metrischer
Raum, Euklidischer
Abstand
Englisch
Barile, Margherita (MathWorld)
Taxicab Metric
Jim Wilson
Overview
of Taxi Cab Geometry
Kardi Teknomo
City
Block Distance, Minkowski
Distance
Pascal Tesson
TAXICAB
GEOMETRY???
Robert M. Dickau
Shortest-path
diagrams, 3D
shortest-path diagrams, Paths
through a 4-D Lattice
The Wolfram Demonstrations Project
Taxicab
Geometry
Wikipedia
Taxicab geometry,
Metric
(mathematics),Euclidean
distance
Referenzen top
(1) Martin Gardner: Geometrie mit Taxis, die Köpfe der Hydra und
andere mathematische Spielereien, Basel 1997
[ISBN 3-7643-5702-9]
Der Originalaufsatz
Taxicab Geometry ist nachzulesen unter
The
Last Recreations: Hydras, Eggs, and Other Mathematical Mystifications
Von Martin Gardner
Zufällig ist das Kapitel 10 im Google-Buch zugänglich.
Feedback: Emailadresse auf meiner Hauptseite
Diese Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2009 Jürgen Köller
top |
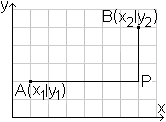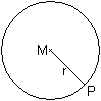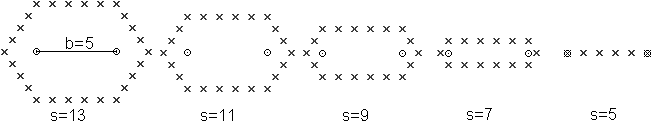
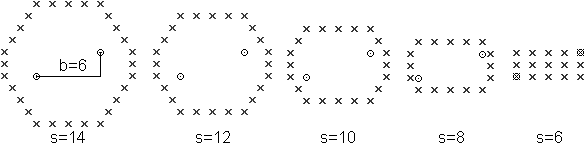
