|
What is Taxicab Geometry?
... ... ... |
Taxicab geometry is a form of geometry, where the distance
between two points A and B is not the length of the line segment AB as
in the Euclidean geometry, but the sum of the absolute differences of their
coordinates.
Formula: AP+PB= |x2-x1| +
|y2-y1|
The points have only integer coordinates in the simple
version and their connections are grid lines. |
... ... ... |
These are the following facts behind the name.
You can consider the grid as a net of streets, which
a taxi driver negotiates.
The crossings are the places, where he can stop.
It is remarkable that the taxi driver - starting in A
- can take different ways, which have the same length, if he is continuously
approaching the destination B. |
If the taxi driver stays on one line of the grid, there is
no difference to the usual geometry.
There are also the names City-Block-,
Manhattan-
oder
Minkowski-Geometrie
beside
Taxicab
Geometry.
Hermann Minkowski (1864 to 1909) had the idea to this
kind of geometry.
The example of this web page
is a chapter in Martin Gardner's book (1).
T-Line Segment
top
There is one line segment to one length in Euclidean
geometry, but several line segments to one length in taxicab geometry.
... ... ... |
This is again shown by the example on the left. Both
lines have the length 9.
You call this new kind of line taxicab-line or
t-line. |
... ... ... |
... ... ... |
There is the question, how many t-line segments are between
two points.
You can count them in this simple case. There are 6 of
them. |
... ... ... |
Looking at the number of t-lines systematically, you
discover a law.
The number of t-line segments on a crossing is always
the sum of the segments at the foregoing crossings.
This leads to Pascal's triangle, whose rows are diagonal
here. |
.. .... .... |
... ... ... |
Point B is on the ninth diagonal and thus on the ninth
row of Pascal's triangle, related to A, and on the fourth place.
There is the number 28+56=84 or "9 choose 3".
There are 84 t-lines for the case "6 to the right, 3 to
the top" to go from A to B.
Generally the number is "n+m choose m" for the case "m
to the right, n to the top". |
T-Line
... ... ... |
For the sake of completeness here is any line between
A and B, which is not a t-line segment.
It consists of the four t-line segments AC, CD, DE and
EB. |
T-Polygon
top
You must also look at polygons in a new way.
... ... ... |
Here are two t-line segments of the length 8 between
the points A and B.
You get a 2-gon, which doesn't exist in the Euclidean
geometry. |
If you give a third point C, it is a question of definition,
whether the points A, B, and C form a triangle.
>Pro: They form a triangle in the Euclidean geometry.
>Against: A, B, and C lie on a t-line.
I follow Martin Gardner (1) on this page, who admits
triangles like this. This is also common knowledge.
In this sense there is also the t-quadrilateral
ADBC in this figure with the side length 4.
Consequently the figure is also a t-16-gon of the side
length 1, though strange enough.
T-Squares?
... ... ... |
You can go a step forward and call the t-quadrilateral
ADBC a t-rhombus, because four sides are equal. It is not a t-square, because
the angle at point D is 180°.
There is a problem in this definition. Many features of
the rhombus get lost, for example the symmetry. |
A quadrilateral is a square, when
all sides are equal und all angles 90° in Euclidean geometry.
... ... ... |
In this sense the quadrilaterals on the left are t-squares.
If you connect the points by straight lines, you get a
rhombus.
Thus is it a t-rhombus and no t-square? |
... ... ... |
If you demand all features of the square, you must only
take the square of the Euclidean geometry as t-square. |
Another access to the square
gives the equation |x|+|y|=2 with D=|R. You can transfer it to taxicab
geometry easily.
You will experience on this
page that this t-square is also a t-circle. This is strange.
T-Line top
... ... ... |
You get a t-line from a t-line segment, if you elongate
the t-line segment over both ends.
You must mind that it goes always upwards (here) or downwards. |
... ... ... |
If you look for points of intersections between two t-lines,
you can have each number of points.
Here the two t-lines intersect in two points. If you change
the ascending (black) t-line in the way that it also goes horizontally
starting at S1, then there are points of intersection without
limits. |
It is not worth to work on t-lines, because there are so
many.
The t-circle and the t-ellipse in the next chapters are
more interesting.
T-Circle top
One circle
... ... ... |
If you give one fixed point M and draw all points, which
have the same distance r from the centre M, you get a circle. |
This statement is transferred
to taxicab geometry.
... ... ... |
If you give one fixed point M and draw all points, which
have the same t-distance 3 from the centre, you get 12 points.
They form a square of the t-side length 6 standing on
one vertex.
More generally:
If you give one fixed point M and draw all points, which
have the same t-distance r from the centre M, you get 4r points.
They form a square of the t-side length 2r standing on
one vertex. |
This reminds one to squaring
the circle, where you must look for a square with the same area as
has a circle.
If the circle is centered
at the origin (0, 0), then the equation is x²+y²=r²
in the Cartesian coordinate system.
In taxicab geometry there is |x|+|y|=r.
...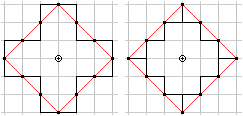 |
Maybe you shouldn't connect the points of the t-circle.
The impression of being a square is lost. |
Two
circles
... ... ... |
Two equal t-circles intersect in all, no one, in one,
or in two points like the usual circles. |
There are more cases with
t-circles.
... ... ... |
Two t-circles with the radii R and r can intersect in
more than two points, for instance in three points here.
In this corner position the number of the points is determined
by the smaller t-radius.
It is n=2r+1 for r<R. |
T-Ellipse top
Horizontal position
... ... ... |
If you give two fixed point F1 und F2
and draw all points, which have the same sum of the distances from
them, you get an ellipse.
The sum is s=s1+s2 in the drawing.
The two points F1 und F2 are called
foci
(singular form is focus). |
The distance b of the foci
and the constant sum s determine the shape of the t-ellipse like the usual
ellipse.
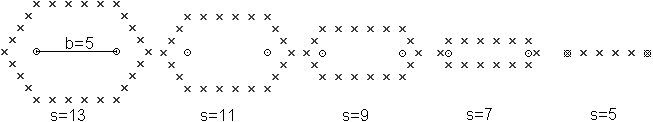
A simple computer program finds out that figures of two
trapezia arise. One pair of parallel sides is as long as the line segment
b=F1F2
. There is only one row in the case s=b=6
with the foci at the ends.

|
here:
b=2, s=6 |
The computer only found t-ellipses, when either
> b and s are even like in the drawing on the left, or
>b and s are odd like in the computer drawings above. |
Explanation: For the left
angular point there is the equation s=2x+b or s-b=2x or "s-b is an
even number".
Thus both, s and b, must be even or odd at the same time.
Diagonal
position
You receive other figures, if the foci lie diagonally.
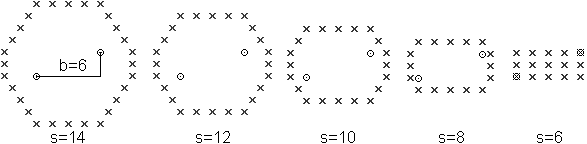
A simple computer program finds out that figures arise,
which have a rectangle 3x5 as a base. There is the complete rectangle 3x5
in the case s=b with the foci at the vertices.
How to get a t-ellipse with
b=6 and s=10

1 The point top right lies on a t-line segment through the
foci. There is (2+6)+2=10.
2 You find five more points with other t-line segments
in the same way.
3 There are six more points for symmetry reasons.
4 There are four more points at the top. The distance
to the right focus is 1 greater step by step, and 1 smaller to the left
focus. - The same thoughts explain the five points at the bottom.
5 You must transfer the same explanation to the points
lying vertically. Here you get two more points, on the left and on the
right.
You can generalize these steps to all t-ellipses.
... ... ...
|
So it results in the fact that the numbers of the horizontal
and vertical points are determined by the points of the slope triangle.
These are the numbers 5 and 3.
Above, the foci lie horizontally. There the two numbers
are 1 and 5, alternatively 1 and 3. |
Addition
... ...are ...are |
The computer program found out that a complete rectangle
3x5 is also a t-ellipse. It is b=s=6.
If the foci are diagonal in the centres of grid squares
as on the left, the result is the same rectangle 3x5, but with b=s=8. |
Outlook top
>There are also investigations about the t-hyperbola
und der t-parabola in Gardner's book. Both curves can also be identified
by distances.
>You can also take triangle patterns instead of square
patterns.
>You can also give a three-dimensional or a higher-dimensional
grid to do taxicab geometry.
Taxicab
Geometry on the Internet top
German
Wikipedia
Manhattan-Metrik,
Französische
Eisenbahnmetrik, Metrischer
Raum, Euklidischer
Abstand
English
Barile, Margherita (MathWorld)
Taxicab
Metric
Jim Wilson
Overview
of Taxi Cab Geometry
Robert M. Dickau
Shortest-path
diagrams, 3D
shortest-path diagrams, Paths
through a 4-D Lattice
The Wolfram Demonstrations Project
Taxicab
Geometry
Wikipedia
Taxicab
geometry,
Metric
(mathematics),
Euclidean
distance
References top
(1) Martin Gardner: Geometrie mit Taxis, die Köpfe
der Hydra und andere mathematische Spielereien, Basel 1997
[ISBN 3-7643-5702-9]
Martin
Gardner: The Last Recreations: Hydras, Eggs, and Other Mathematical Mystifications
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de
©
2009 Jürgen Köller
top |
 ...
... ...
... ...
... ...
... ...
... ...
... ....
.... ...
... ...
... ...
... ...
... ...
...

 ...
... ...
... ...
... ...
...
 ...
... ...
... ...
...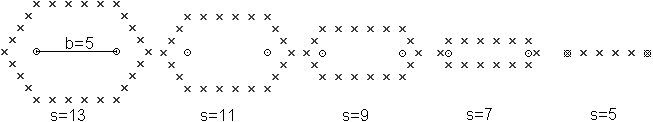

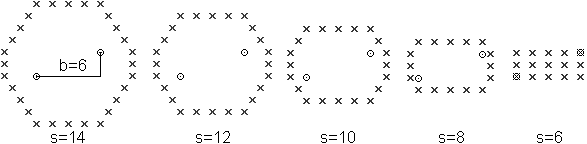

 ...
... ...are
...are