Sinus hyperbolicus

Inhalt dieser Seite

Was ist Sinus hyperbolicus?
Kurvendiskussion
Einordnung
Kosinus hyperbolicus
Hinweis auf die Namen

Umkehrfunktion von sinh
Reziproke Funktion von sinh
Reihenentwicklung von sinh
Sinus hyperbolicus im Internet
Referenzen.

Zur Hauptseite "Mathematische Basteleien"

Was ist Sinus hyperbolicus?
Sinus hyperbolicus (sinh) ist eine Funktion, die mit Hilfe der Exponentialfunktion definiert wird.

f(x) = sinh(x) = (1/2)(e^x-e^-x)

Kurvendiskussion top
Die Funktion ist stetig und differenzierbar im Definitionsbereich D = |R.

Vorweg die Ableitungen
f(x) = (1/2)(e^x-e^-x)
f '(x) = (1/2)(e^x+e^-x)
f ''(x) = (1/2)(e^x-e^-x) = f(x)
f '''(x) = (1/2)(e^x+e^-x)

...

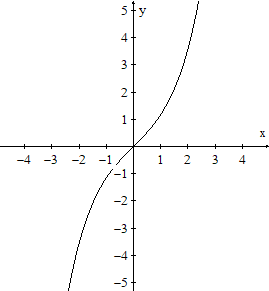- Der Wertebereich für D=|R ist auch die Menge der reellen Zahlen.
- Es gibt keine Extremstelle, denn es gilt f '(x)>0.
- Der Nullpunkt ist Kurvenpunkt und gleichzeitig Wendepunkt.
- Es gilt nämlich f(0) = 0 und f ''(0) = 0, f '''(x) = 1.
- Die Steigung im Nullpunkt ist 1.
- Geht x gegen Unendlich, so geht f(x) = (1/2)(e^x-1/e^x) gegen (1/2)e^x.
- Geht x gegen minus Unendlich, so geht f(-x) = (1/2)(1/e^x-e^x) gegen -(1/2)e^x.
- Der Graph ist punktsymmetrisch, denn es gilt -f(-x) = -(1/2)(e^-x-e^x) = f(x).
- Der Graph ist monoton steigend.

Einordnung top
Die Funktion sinh gehört zu den sechs Hyperbelfunktionen oder hyperbolischen Funktionen.

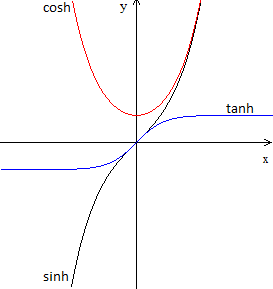... Sinus hyperbolicus sinh(x) = (1/2)(e^x-e^-x)
Kosinus hyperbolicus cosh(x) = (1/2)(e^x+e^-x)
Tangens hyperbolicus tanh(x) = (e^x-e^-x)/(e^x+e^-x)

...
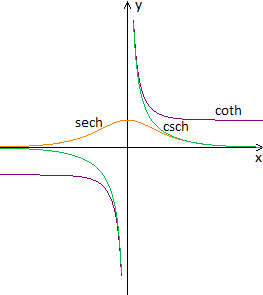Kotangens hyperbolicus coth(x) = (e^x+e^-x)/(e^x-e^-x)
Sekans hyperbolicus sech(x) = 2/(e^x+e^-x)
Kosekans hyperbolicus csch(x) = 2/(e^x-e^-x)

Kosinus hyperbolicus top

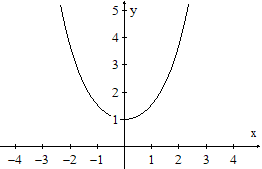... Zum Graphen der Funktion Kosinus hyperbolicus (cosh(x) =(1/2)(e^x+e^-x) gibt es bei mir die Webseite Kettenlinie. Eine beidseitig aufgehängte Kette wird nämlich im Prinzip durch die Funktion mit f(x) = (1/2)(e^x+e^-x) beschrieben.

Im nächsten Kapitel benötigt man die Umkehrfunktion des Kosinus hyperbolicus.
Der Ansatz ist y = (1/2)(e^x+e^-x).
Daraus folgt 2y = e^x+e^-x oder 2ye^x = (e^x)²+1 oder (e^x)²-2ye^x+1 = 0.
Das ist eine quadratische Gleichung mit der Lösung e^x = y+sqrt(y²-1). Das Minuszeichen fällt weg, da e^x>0 ist.
Die Variablen x und y werden vertauscht: e^y = x+sqrt(x²-1) oder y = ln[x+sqrt(x²-1)].
Ergebnis: Die Umkehrfunktion der Funktion cosh ist g(x) = ln[x+sqrt(x²-1)] für D=|R⁺.

Hinweis auf die Namen top
Es stellt sich die Frage, weshalb für die Funktionen die Namen der Kreisfunktionen Sinus, Kosinus, Tangens usw. gewählt wurden und wie es zum Eigenschaftswort "hyperbolicus" kam. Bekannt und überzeugend ist da die folgende Gegenüberstellung.

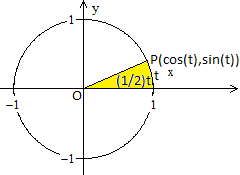
Der Einheitskreis mit x²+y² = 1 und die Einheitshyperbel mit x²-y² = 1 werden verglichen. Ein beliebiger Punkt P bewege sich in beiden Fällen auf der x-Achse beginnend auf den Kurven nach oben. Seine Lage wird durch die Parameterdarstellung x=cos(t), y=sinh(t) bzw. x=cosh(t), y=sin(t) beschrieben. Dabei überstreicht der Strahl OP jeweils die Fläche (1/2)t.

Begründungen zum Kreis
Es sei t das Bogenmaß eines beliebigen Winkels im Einheitskreis.
Dann ist x=cos(t), y=sin(t) die Parameterdarstellung des Kreises, denn es gilt x²+y² = cos²(t)+sin²(t) =1.
Für den Flächeninhalt A des gelben Flächenstücks gilt A:t = pi : 2pi oder A = (1/2)t.

Begründungen zur Hyperbel
Die Hyperbel hat die Parameterdarstellung x=cosh(t), y=sinh(t), denn es gilt x²-y² = (1/4)(e^t+e^-t)²-(1/4)(e^t-e^-t)² = ... = 1.

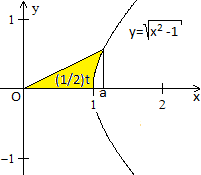...	Für den Flächeninhalt A des gelben Flächenstücks gilt

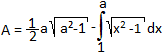In einer Sammlung von Integralen findet man

.
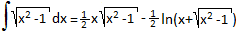Dann ist
A = (1/2)a*sqrt(a²-1)-[(1/2)x*sqrt(x²-1)-(1/2)ln(x+sqrt(x²-1))]_a¹
A = (1/2)a*sqrt(a²-1)-(1/2)a*sqrt(a²-1)+(1/2)ln(a+sqrt(a²-1))-0
A = (1/2)ln[a+sqrt(a²-1)]
A = (1/2)arcosh(a).
Das bedeutet a=2A oder A=(1/2)a.

Damit sind die Zeichnungen erklärt.

Es gibt viele weitere Belege. So lassen sich zahlreiche Formeln der Trigonometrie auf die hyperbolischer Funktionen übertragen (2).
Ich verzichte darauf, auf sie einzugehen.

Umkehrfunktion von sinh top

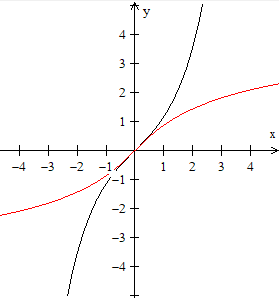...... Die Funktion sinh ist monoton steigend. Dann erhält man den Graphen der Umkehrfunktion, indem man den Graphen der Ausgangsfunktion an der ersten Winkelhalbierenden spiegelt.
Die Funktionsgleichung der Umkehrfunktion erhält man auf dem gleichen Wege wie die von cosh.
- Man geht aus von der Gleichung y=(1/2)(e^x-e^-x).
- Man gelangt zu der quadratischen Gleichung (e^x)²-2ye^x-1 = 0.
- Die Lösung ist e^x = y+sqrt(y²+1).
- Die Variablen x und y werden vertauscht, e^y = x+sqrt(x²+1).
- Die Funktionsgleichung ist y = ln[x+sqrt(x²+1)].

Die Umkehrfunktionen von sinh und cosh gehören zu den Areafunktionen.
Deshalb heißen sie arsinh(x) = ln[x+sqrt(x²+1)] und arcosh(x) = ln[x+sqrt(x²-1)].

Reziproke Funktion von sinh top

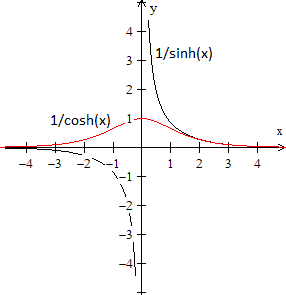... Die reziproke Funktion von sinh hat den Funktionsterm 1/sinh(x).
Es gilt r₁(x) = 2/(e^x-e^-x) = csc(x).
Die Umkehrfunktion von cosh(x)=(1/2)(e^x+e^-x) hat die Gleichung r₂(x) = 2/(e^x+e^-x) = sech(x).
Der Graph ist eine Glockenkurve.

Der Grenzwert des Flächeninhalts der Fläche zwischen der x-Achse und der roten Kurve ist pi. (2)

Reihenentwicklung von sinh top

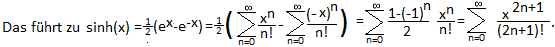
Dabei ist der Term (1/2)[1-(-1)ⁿ] gleich 0, wenn n eine gerade Zahl ist und gleich 1, wenn n ungerade ist.

Die ersten Summanden sind sinh(x) = x+x³/6+x⁵/120+x⁷/5040+... .

In diesem Zusammenhang sind die folgenden Reihen bemerkenswert.
artan(x) = x+x³/3+x⁵/5+x⁷/7+ ...
arctan(x) = x-x³/3+x⁵/5-x⁷/7+ ...

Sinus hyperbolicus im Internet top

Deutsch

Wikipedia
Sinus hyperbolicus und Kosinus hyperbolicus, Hyperbelfunktion

Englisch

Eric W. Weisstein (MathWorld)
Hyperbolic Sine, Hyperbolic Cosine, Hyperbolic Functions

Wikipedia
Hyperbolic function, Inverse hyperbolic functions, List of integrals of hyperbolic functions, Sigmoid function, Hyperbolic triangle

Referenzen top
(1) Wilhelm Leupold (u.a.): Analysis für Ingenieur- und Fachschulen, Frankfurt/M Zürich 1966 , Seite 205 ff.
(2) https://de.wikipedia.org/wiki/Sinus_hyperbolicus_und_Kosinus_hyperbolicus

Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
https://www.mathematische-basteleien.de/

top
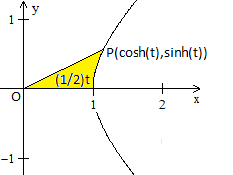
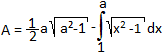