|
Was ist eine Glockenkurve?
...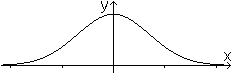 ... ... |
Die Glockenkurve ist der Graph der Funktion mit f(x)=e-x².
Dafür schreibt man auch f(x)=exp(-x²).
Der Definitionsbereich ist D=|R, der zugehörige
Wertebereich W={y|0<y<=1}. |
Die Glockenkurve ist der Graph der Gauß-Funktion, die
in der Wahrscheinlichkeitsrechnung eine Rolle spielt.
Der Term exp(-x²) ist wohl ihr einfachster Term.
Für diese Webseite habe
ich Kurven mit gleichem Aussehen gesucht und etliche Klassiker gefunden.
Gaußsche
Glockenkurve top
Kurvendiskussion
f(x) = exp(-x²)
f '(x) = (-2x)exp(-x²)
f ''(x) = -2exp(-x²)+(-2x)(-2x)exp(-x²) = (4x²-2)exp(-x²)
In x=0 ist eine Hochstelle, denn es gilt
f '(0)=0 und f ''(0) = -2e0<0.
Für eine Wendestelle
muss gelten: f ''(x)=0 und f '''(x) ungleich 0.
f''(x)=0 führt zu 4x²-2=0 oder x1=(1/2)sqrt(2)
und x2=-(1/2)sqrt(2).
Das sind die Wendestellen. Auf die Einbeziehung der 3.Ableitung
verzichte ich.
Die Wendepunkte sind W1[(1/2)sqrt(2)|1/sqrt(e)]
und W2[-(1/2)sqrt(2)|1/sqrt(e)].
Es gilt exp(-x²)=1/exp(x²).
Dadurch erklärt sich das Verhalten im Unendlichen.
Es gilt f(-x)=f(x). Dadurch
erklärt sich die Achsensymmetrie des Graphen.
Drei Graphen
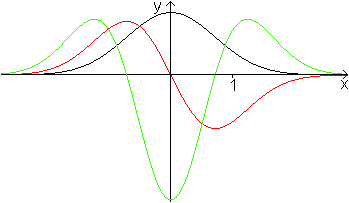
|
f(x)=exp(-x²)
f '(x)=(-2x)exp(-x²)
f ''(x)=(4x²-2)exp(-x²) |
Fläche
unter der Kurve
Die Funktion mit f(x)=exp(-x²) hat keine elementare
Stammfunktion.
Will man das Integral näherungsweise bestimmen,
so führt die Reihenentwicklung zum Ziel.
Es gilt exp(x) = 1+x+x²/2!+x³/3!+... und folglich
exp(-x²)=1-x2+x4/2!-x6/3!+-... .
Daraus ergibt sich für das Integral
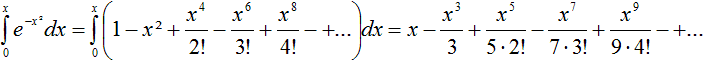
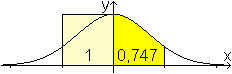
Beispiel: Die Fläche
unter der Kurve von x=0 bis x=1
Zum Vergleich ist ein Einheitsquadrat eingezeichnet.
Die Bestimmung der Gesamtfläche
unter der Glockenkurve führt zu einem uneigentlichen Integral mit
einem Grenzwert.
Die Bestimmung ist umfangreich
und nicht mehr auf (bei mir üblichem) Schulmathematik-Niveau.
Man findet die Herleitung der nebenstehenden Formel bei
Lite
Tube (URL unten) in einem Videoclip.
Parametergleichungen
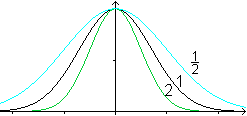
fa(x)=2*exp(-ax²)
|
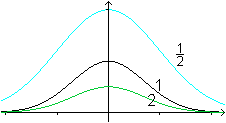
fb(x)=b*exp(-x²)
|
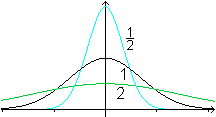
fc(x)=(1/c)*exp(-c²x²)
|
Gauß-Funktion
Die Glockenkurve ist der Graph der Gauß-Funktion,
der Dichtefunktion der Normalverteilung.
...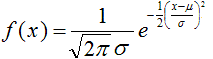 ... ... |
Das ist die Gleichung der Gauß-Funktion in der
allgemeinen Form.
Der Parameter sigma² ist die Varianz; x=mü
gibt die Lage des Maximums an. |
Weitere Glockenkurven
top
Reziproke Funktionen
Ersetzt man den Funktionsterm einer Funktion durch ihren
Kehrwert, entsteht eine neue Funktion,
die reziproke Funktion.
...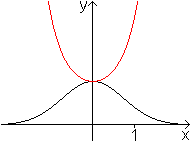 ... ... |
Der Kehrwert von exp(-x²) ist exp(x²).
Die reziproke Funktion hat
mit der Ausgangsfunktion den Punkt P(0|1) gemeinsam. Aus dem Hochpunkt
wird ein Tiefpunkt, Wendepunkte gibt es nicht und die Funktionswerte gehen
mit x über alle Grenzen. |
Hier ist ein Ansatz, weitere
"Pseudo-Glockenkurven" zu finden.
...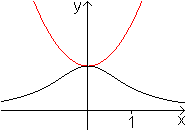 ... ... |
Zur Parabel mit y=x²+1 gehört eine Glockenkurve.
Sie ist der Graph der reziproken Funktion mit r(x)=1/(x²+1).
Sie ist ein Sonderfall der Versiera
der Maria Agnesi. |
Versiera
der Maria Agnesi
..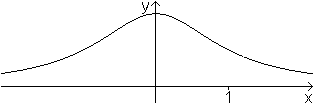 .... .... |
Der Graph hat die Darstellung y=a³/(x²+a²),
wobei der Parameter a eine reelle Zahl ist. In der Zeichnung ist a=1, und
somit heißt die Gleichung y=1/(x²+1).
Das ist eine algebraische Kurve dritter Ordnung. |
Eine
Folge von Glockenkurven.
Die Funktion y=1/(x2+1) kann man verallgemeinern
zu y=1/(x2n+1). Dabei ist n eine natürliche Zahl.
...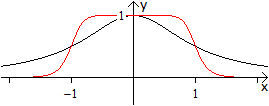 ... ... |
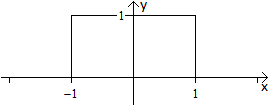 ... ... |
In der Zeichnung sind n=1 und n=5.
Je größer die Zahl n wird, desto mehr nähert
sich der Graph der abgebildeten Rechteckkurve, erreicht sie aber
nie. |
Ein
gebrochenrationale Funktion
...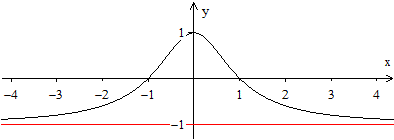 ... ... |
Die gebrochenrationale Funktion ist y=(1-x²)/(1+x²).
Sie hat die Asymptote y=-1. |
Sekans
Hyperbolicus
...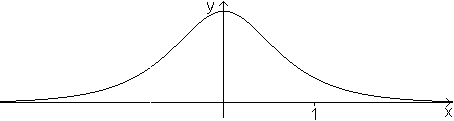 ... ... |
Die Funktionsgleichung ist y=4/[exp(x)+exp(-x)].
Die reziproke Funktion ist bis auf einen Faktor der bekanntere
Kosinus Hyperbolicus.
cosh(x)=(1/2)[exp(x)+exp(-x)].
|
Chonchoide
von de Sluze (Muschelkurve von de Sluze)
...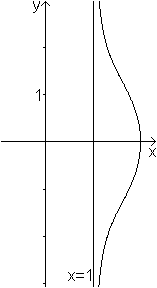 ... ... |
Der Graph hat die Darstellung (x-1)(x²+y²)=ax²,
wobei der Parameter a eine reelle Zahl ist. In der Zeichnung ist a=1 und
somit heißt die Gleichung (x-1)(x²+y²)=x².
Das ist eine algebraische Kurve dritter Ordnung. |
Külpsche
Quartik
...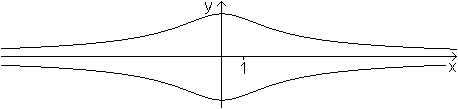 ... ... |
Der Graph hat die Darstellung x²y²=a²(a²-y²),
wobei der Parameter a eine reelle Zahl ist. In der Zeichnung ist a=2 und
somit heißt die Gleichung x²y²=16-4y².
Das ist eine algebraische Kurve vierter Ordnung. |
Die Kurve hat auch die einfache Parameterdarstellung x=2tan(t)
/\ y=2cos(t).
"Fermat
cubic"
...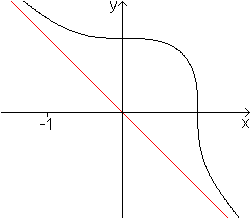 ... ... |
Der Graph hat die Darstellung x³+y³=1.
Das ist eine algebraische Kurve dritter Ordnung. |
Krümmung
der Normalparabel
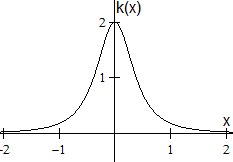 |
k(x) = y''/(1+y'²)3/2
= 2/(1+4x²)3/2
Mehr auf meiner Webseite Evolute |
Glockenkurven
im Intervall top
Eine biquadratische Funktion
...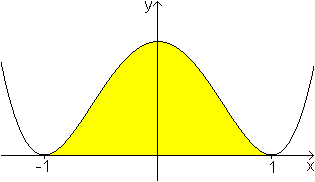 ... ... |
Der Graph der Funktion mit g(x)=x4-2x2+1
oder g(x)=(x-1)2(x+1)2 hat im Definitionsbereich
D={x|-1<=x<=+1} fast die gleichen Eigenschaften wie die Glockenkurven
oben.
Er hat auch einen Hochpunkt und zwei Wendepunkte. Ein
Unterschied besteht darin, dass dieser Graph nicht die x-Achse als Asymptote
hat, sondern sie berührt. |
Man kann Kurven dieser Art
auch als Glockenkurven im weiteren Sinn bezeichnen.
Sinus-Quadrat-Kurve
Der Graph der Funktion mit g(x)=sin²(x) ist zwischen
zwei Berührpunkten eine Glockenkurve.

Sinuskurve
... ... ... |
Ein Teilstück einer Sinuskurve ist eine Glockenkurve.
Es gilt y=sin(x) mit D={x|-(1/2)pi<=x<=(3/2)pi}. |
Dumbbell-Kurve
...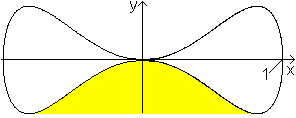 ... ... |
Der Graph hat die Darstellung (a²)²y²=(x²)²(a²-x²),
wobei der Parameter a eine reelle Zahl ist. In der Zeichnung ist a=1 und
somit heißt die Gleichung y2-x4(1-x2)=0.
Das ist eine algebraische Kurve vierter Ordnung. |
Plückersche
Quartik
... ... ... |
Der Graph hat die Darstellung (x²-a²)+(y²-a²)=(b²)²,
wobei die Parameter a und b reelle Zahlen sind. In der Zeichnung ist a=1
und (b²)²=2,5. Somit heißt die Gleichung (x²-1)+(y²+1)=2,5.
Das ist eine algebraische Kurve zweiter Ordnung. |
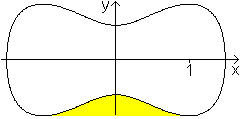
Glockenkurve
aus Kreisteilen
...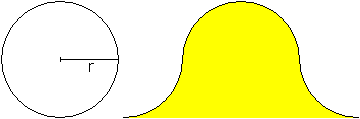 ... ... |
Ein Halbkreis und zwei Viertelkreise bilden eine Glockenkurve. |
...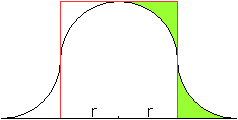 ... ... |
Das Besondere ist, dass die Fläche unter der Glockenkurve
denselben Flächeninhalt hat wie das Quadrat mit der Seitenlänge
2r.
Es ist bemerkenswert, dass die Kreiszahl pi in der Flächenformel
A=4r² nicht auftaucht. |
... ... ... |
Nach der gleichen Methode kann auch aus Teilen
der Normalparabel eine Glockenkurve gebildet werden. |
Glockenkurve
- dreidimensional top
.
.
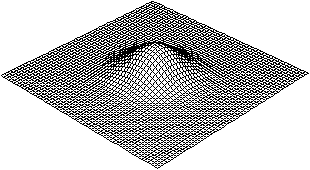
.z=exp(-x²-y²)
|
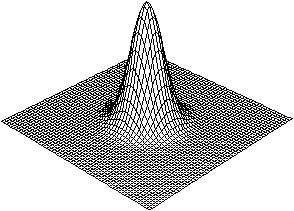
z=4exp(-2x²-2y²)
|
Glockenform top
...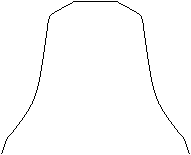 ... ... |
Die Querschnittlinie einer Glocke lässt sich nicht
durch eine einfache Formel beschreiben.
Die Form ist aus der Praxis heraus in den Zeitläufen
entstanden.
Das Ziel war, einen lauten, schönen und wohl definierten
Klang zu erzeugen.
Die Skizze habe ich nach einer Glocke in Bad Salzuflen-Schötmar
erstellt. |
... ... ... |
Die Glocke aus Eisen steht im Schatten der Kilianskirche
in Schötmar.
Sie stammt aus der Zeit nach dem 1.Weltkrieg und war zu
schwer für den Turm. Deshalb wurde sie (und eine zweite) 1989 durch
je eine Bronzeglocke ersetzt.
Quelle: http://www.schoetmar.net/?id=17
|
Glockenkurven
im Internet top
Deutsch
Jörn Loviscach (Lite Tube)
Fläche
unter Gauß-Glocke (Video bei Youtube)
Wikipedia
Normalverteilung,
Glocke,
Konchoide
von de Sluze, Versiera
der Agnesi,
Sinus
Hyperbolicus und Kosinus Hyperbolicus
Englisch
Eric W. Weisstein (MathWorld)
Conchoid
of de Sluze, Witch
of Agnesi, Dumbbell
Curve
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Normal
distribution,
Bell
(instrument), Conchoid
of de Sluze, Witch
of Agnesi
Französisch
Robert FERRÉOL (MathCurve)
COURBE
DE GAUSS, SÉCANTOÏDE
HYPERBOLIQUE, CUBIQUE
CIRCULAIRE FOCALE,
QUARTIQUE
DE KÜLP, LINTÉAIRE
DROITE
Referenzen top
(1) W. Leupold (Hrsg.): Analysis für Ingenieur-
und Fachschulen,
Verlag Harry Deutsch,
Frankfurt/M und Zürich, 1966
(2) Robert FERRÉOL: http://www.mathcurve.com/courbes2d/courbes2d.shtml
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2013 Jürgen Köller
top |
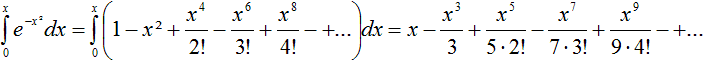

 ...
...
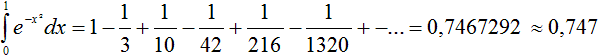
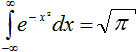



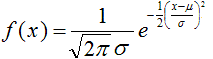 ...
... ...
... ...
... ....
.... ...
... ...
... ...
... ...
... ...
... ...
... ...
...
 ...
... ...
... ...
... ...
... ...
... ...
... ...
...

 ...
... ...
...