|
Was ist das pascalsche Dreieck?
...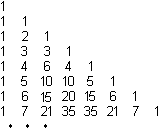 ... ...
|
...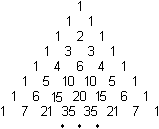 ... ...
|
Das pascalsche Dreieck ist eine Anordnung von Zahlen
in Dreiecksform,
konstruiert nach einem einfachen Bildungsgesetz. |
Konstruktion
top
1
1 1
|
....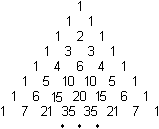 .. .. |
Das Bildungsgesetz lautet wie folgt.
Man geht von einem Dreieck aus drei Einsen aus.
Die folgenden Zeilen beginnen und enden auch mit einer
Eins.
Dazwischen liegen Zahlen, die sich als Summe der beiden
darüber liegenden Zahlen ergeben.
So kann das Dreieck nach unten hin beliebig weit fortgesetzt
werden. |
Binomialkoeffizient
top
Die Zahlen des pascalschen Dreiecks
gehen also sukzessive auseinander hervor.
.. .... .... |
Es gibt aber auch die Möglichkeit,
sie unabhängig voneinander als sogenannte Binomialkoeffizienten zu
berechnen.
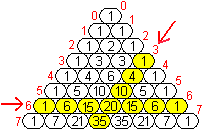
So erhält man die Zahl 20
in der horizontal liegenden 6. Zeile und in einer schräg liegenden
3. Spalte wie folgt.
.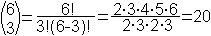 .. .. |
Man liest das Klammersymbol als "6 über 3".
Auf dieser Seite heißt der Term auch C(6,3). |
|
| Allgemein wird die Zahl in der n-ten Zeile und der k-ten
Spalte nach der Formel |
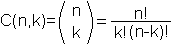 |
berechnet. |
Die Formel geht auf Euler zurück. Sie wurde in einem
ganz anderen Zusammenhang gefunden.
Sie gibt an, auf wie viele verschiedene Arten man k Objekte
aus einer Menge von n verschiedenen Objekten ohne Beachtung der Reihenfolge
und ohne Zurücklegen auswählen kann.
Diese Anzahl ist z.B. beim Lottospiel von Interesse,
wo es darum geht, aus den ersten 49 Zahlen "6 Richtige" zu finden.
Mehr auf meiner Seite 13
983 816.
Der Term C(n,k) ermöglicht
es, das Konstruktionsprinzip C(n,k-1)+C(n,k)=C(n+1,k) des pascalschen Dreiecks
nachzuvollziehen.
Jede Zahl ist die Summe der beiden darüber liegenden
Zahlen.
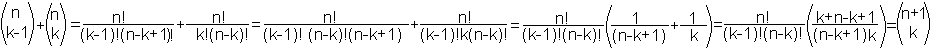 Der Vollständigkeit halber sind noch die Ränder
des Dreiecks mit C(0,0)=C(n,0)=C(n,n)=1 festzulegen.
Der Vollständigkeit halber sind noch die Ränder
des Dreiecks mit C(0,0)=C(n,0)=C(n,n)=1 festzulegen.
Die Symmetrie des pascalschen
Dreiecks ergibt sich aus der Identität C(n.k)=C(n,n-k), wie man leicht
nachrechen kann.
Binomischer Lehrsatz
top
Es geht beim binomischen Lehrsatz darum, die Potenz einer
zweigliedrigen Summe in eine Summe zu verwandeln.
Der einfachste Fall ist die binomische
Formel (a+b)²=a²+2ab+b².
Für die Potenzen (a+b)n ergibt sich für
n=2, ... , 7.
|
(a+b)2 =
(a+b)3 =
(a+b)4 =
(a+b)5 =
(a+b)6 =
(a+b)7 =
|
a2+2ab+b2
a3+3a2b+3ab2+b3
a4+4a3b+6a2b2+4ab3+b4
a5+5a4b+10a3b2+10a2b3+5ab4+b5
a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6
a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7
|
Siehe da, die Vorzahlen bilden bei geschickter Anordnung
der Summanden das pascalsche Dreieck.
Allgemein gilt: (a+b)n=C(n,0)anb0+C(n,1)an-1b1+C(n,2)an-2b2+...+C(n,n-2)a2bn-2+C(n,n-1)a1bn-1+C(n,n)a0bn.
Für einen Beweis dieser Formel wendet man die Methode
der vollständigen Induktion an.
Das wird auf der englischsprachigen Wikipedia-Seite Binomial
theorem (URL unten) vorgeführt.
Der oben eingeführte
Name Binomialkoeffizient für C(n,k) findet hier
also eine Erklärung.
Sonderfall
... ... ...
|
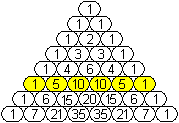
Setzt man a=b=1, so ist 2n gleich die Summe
der Zahlen in der n-ten Zeile ist.
1+5+10+10+5+1 = 25
C(n,0)+C(n,1)+C(n,2)+...+C(n,n-2)+C(n,n-1)+C(n,n) = 2n
|
Pascalsche Zahlen
top
In diesem Abschnitt werden u.a. einige Aussagen eines
Aufsatzes aus "Bild der Wissenschaft" von 1965 wiedergegeben (1).
Offenbar verwendete der Verfasser damals nicht den Computer.
Definition
...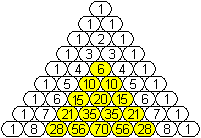 ... ... |
Lässt man beim pascalschen Dreieck die Einsen am
Rande und die natürlichen Zahlen in den ersten Spalten weg, so bleiben
die pascalschen Zahlen übrig.
Die ersten Zahlen sind 6, 10, 15, 20, 21, 28, 35, 36,
45, 55, 56, 66, 70, 78, 84, 91, 105, 120, 126, 136, 153, 165, 171, 190,
210, 220, 231, 252, 253, 276, 286, 300, 325, 330, 351, 364, 378, 406, 435,
455, 462, 465, 495, 496, 528, 560, 561, 595, 630, 666, 680, 703, 715, 741,
780, 792, 816, 820,... |
Anzahl
der pascalschen Zahlen bis zur 100.Zeile
... ... ... |
Vorweg eine Beschränkung auf die ersten acht
Zeilen.
Die Anzahl der Zahlen bestimmt man durch folgende Überlegung.
>Die Anzahl der markierten Zahlen ist 1+2+3+4+(8-3)=(5*6):2=15.
>(8-2):2=3 Zahlen in der vertikalen Symmetrieachse kommen
einmal vor.
>15-3=12 Zahlen kommen doppelt vor. Das führt zu
12:2=6 Zahlen.
Insgesamt gibt es also 6+3=9 Zahlen. |
Diese Anzahl konnte man natürlich direkt durch Abzählen
erhalten. Aber so kann man verallgemeinern.
Man
erhält die Anzahl der Zahlen der ersten 100 Zeilen, indem man die
Zahl 8 durch 100 ersetzt.
>Die Anzahl der markierten Zahlen ist 1+2+...+(100-3)=(97*98):2=4753.
>(100-2):2=49 Zahlen kommen längs der vertikalen
Symmetrieachse einmal vor.
>4753-49=4704 Zahlen kommen doppelt vor. Das führt
zu 4704:2=2352 Zahlen.
Insgesamt gibt es danach also 2352+49=2401 Zahlen.
Diese Zahl ist noch herabzusetzen,
denn es gibt weitere, gleiche Zahlen im Dreieck, die nicht in einer Zeile
liegen.
C(16,2)=C(10,3)
=120
|
C(21,2)=C(10,4)
=210
|
C(56,2)=C(22,3)
=1540
|
C(78,2)=C(15,5)
=C(14,6)
=3003
|
C(120,2)=C(36,3)
=7140
|
C(153,2)=C(19,5)
=11628
|
C(221,2)=C(17,8)
=24310
|
Verteilung
der pascalschen Zahlen
Nach (1) gibt es
eine einstellige Zahl (die Sechs)
15 zweistellige Zahlen |
48 dreistellige Zahlen
135 vierstellige Zahlen |
393 fünfstellige Zahlen
1140 sechsstellige Zahlen |
3398 siebenstellige Zahlen
. |
Unter den ersten 10 000 000 Zahlen gibt es also nur 1+15+48+135+393+1140+3398=5130
pascalsche Zahlen.
Das sind nur 5130:10.000.000=0,000513 % aller Zahlen.
Muster
im pascalschen Dreieck top
Wegen der Fakultäten in C(n,k) = n!/[k!(n-k)!] sind
die pascalschen Zahlen reich an Teilern.
In (1) wird als typische Zahl C(27,8)=2.220.075=33*52*11*13*23
angegeben.
Offenbar hat die Verteilung
der Teiler System. Es ist nämlich bemerkenswert, dass auf der Spitze
stehende Dreiecke entstehen, wenn man Zahlen mit gleichen Teilern markiert.
Hier sind die Muster für einfache Teiler.
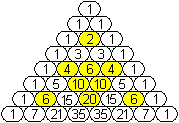
teilbar durch 2
|
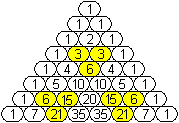
teilbar durch 3
|
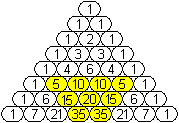
teilbar durch 5
|
Die Muster werden eindrucksvoller, wenn man mehr Zeilen betrachtet.
Ich verweise dazu auf die Applets von Arndt Brünner und shodor.org
(URL unten).
Sehenswert:

teilbar durch 7
Folgen
im pascalschen Dreieck top
Dreieckszahlen
...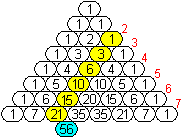 ... ...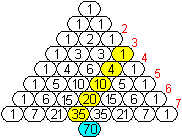 ... ... |
In den Spalten stehen Folgen, nämlich
> in der 0.Spalte die stagnierende Folge von Einsen,
> in der 1.Spalte die Folge der natürlichen Zahlen,
> in der 2. Spalte die Folge der Dreieckszahlen,
> in der 3. Spalte die Folge der Tetraederzahlen,
> in der 4. Spalte die Folge der Zahlen zum 4.dimensionalen
Tetraeder,
> in der 5. Spalte die Folge der Zahlen zum 5.dimensionalen Tetraeder
usw. |
Es besteht ein Zusammenhang zwischen den Folgen.
Jede rechts neben einer Folge liegende Folge ist immer
die Folge der Partialsummen der vorhergehenden.
Z.B. ist die Dreiecksfolge 1, 3, 6, 10, 15, ... auch
die Summenfolge 1, 1+2, 1+2+3, 1+2+3+4, 1+2+3+4+5, ....
So ist erklärlich, dass in der obigen Zeichnung
die Summe der Zahlen in den gelben Feldern gleich der Zahl im blauen Feld
ist.
Catalan-Zahlen
Die Catalan-Zahlen geben an, in
wie viele Dreiecke ein n-Eck durch die Diagonalen
aufgeteilt wird.
Die ersten Glieder der Folge sind
1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, ... (Sloane's A000108).

Zum Fünfeck gehört die Catalan-Zahl 5.
|
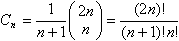
Bildungsgesetz
|
... ... ... |
Die Folge der Catalan-Zahlen ist im pascalschen Dreieck
abzulesen, indem man in einer Zeile jeweils die Differenz aus der Zahl
auf der Symmetrieachse und der übernächsten Zahl bildet.
Das sind 1, 2, 6-1, 20-6, 70-28, ... |
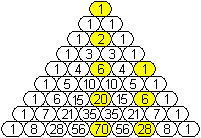
Fibonacci-Folge
Die Fibonacci-Folge entsteht, wenn
jedes Glied der Folge als Summe der beiden vorhergehenden Glieder berechnet
wird.
Auszugehen ist dabei von den ersten
beiden Gliedern 1,1. Das führt zu 1, 1, 2, 3, 5, 8, 13, 21,
34, 55, ...
(Das erinnert an die Konstruktion
des pascalschen Dreiecks oben.)
...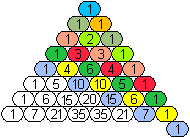 ... ... |
Die Glieder der Folge sind im pascalschen Dreieck vom
3.Glied an als Summen enthalten.
Das sind die Summen aus diagonal liegenden Zahlen.
1+1=2, 2+1=3,
1+3+1=5, 3+4+1=8,
1+6+5+1=13, 4+10+6+1=21,
1+10+15+7+1=34, ... |
Harmonisches Dreieck
top
...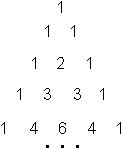 ... ... |
Das harmonische Dreieck oder Leibniz-Dreieck geht aus
dem pascalschen Dreieck hervor. |
...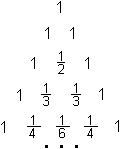 |
In einem ersten Schritt bildet man die Kehrwerte der
Zahlen.
D.h., man ersetzt jede Zahl z durch 1/z. |
...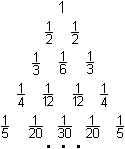 ... ... |
In einem zweiten Schritt dividiert man die Zahlen jeder
Zeile durch die um 1 vermehrte Nummer der Zeile,
d.h., die Zahl in der nullten Zeile durch 1, die in der
erste Zeilen durch 2, die in der zweiten Zeile durch 3 usw.
So entsteht das harmonische Dreieck. |
Die Zahlen C(n,k) des pascalschen
Dreiecks werden also durch 1/[(n+1)C(n,k)] ersetzt.
Das Besondere ist, dass im
harmonischen Dreieck jede Zahl die Summe der beiden darunter liegenden
Zahlen ist.
Das heißt in der Formelsprache 1/[(n+1)C(n,k)]
= 1/[(n+2)C(n+1,k)]+1/[(n+2)C(n+1,k+1)].
Bestätigung:
1/[(n+2)C(n+1,k)]+1/[(n+2)C(n+1,k+1)] =
[k!(n+1-k)!]/[(n+2)(n+1)!]+[(k+1)!(n-k)!]/[(n+2)(n+1)!]
= [k!(n-k)!]/[(n+1)n!]{(n+1-k)/(n+2)+(k+1)/(n+2)} =[k!(n-k)!]/[(n+1)n!]
=1/[(n+1)C(n,k)]
Pascalsches
Dreieck im Internet top
Arndt Brünner
Muster
im Pascalschen Dreieck
Frederik Schäfer
Poissionverteilung,
Binomialverteilung und Hypergeometrische Verteilung
Manfred Börgens (Mathematik auf Briefmarken)
Blaise
Pascal (1623 - 1662), Das
Pascal'sche Dreieck mit alten chinesischen Dezimalzahlen
Matroids Matheplanet
Das
Pascalsche Dreieck, Das
trinomische Dreieck
Michael Holzapfel
Das
Pascalsche Dreieck
Walter Fendt
Binomialkoeffizienten
und Pascalsches Dreieck (Applet)
Wikipedia
Pascalsches
Dreieck, Binomischer
Lehrsatz, Binomische
Reihe, Binomialkoeffizient,
Sierpinski-Dreieck,
Fibonacci-Folge,
Catalan-Zahlen,
Harmonisches
Dreieck
Englisch
Eric W. Weisstein (MathWorld)
Pascal's
Triangle, Pascal's
Formula, Binomial
Coefficient, Binomial
Sums, Sierpinski
Sieve, Tetrix,
Number
Triangle
Math Forum
Pascal's
Triangle: Binomial
Coefficient, Probability
and Combinations, Sierpinski
Triangle
shodor.org
Coloring
Multiples in Pascal's Triangle
The
On-Line Encyclopedia of Integer Sequences
Binomial coefficients: C(n,k), 2 <= k <= n-2, sorted,
duplicates removed. (A006987)
Numbers that occur 5 or more times in Pascal's triangle
(A003015)
Wikipedia
Pascal's
triangle, Pascal's
rule, Binomial
theorem, Binomial
series, Binomial
coefficient, Star
of David theorem,
Sierpinski
triangle, Fibonacci
number, Catalan
number, Leibniz
harmonic triangle
Referenzen
top
(1) Siegfried Rösch: Neues vom Pascal-Dreieck, Bild
der Wissenschaft, September 1965 (Seite 758ff.)
(2) Martin Gardner: Mathematischer Karneval, Frankfurt
am Main, 1975 [ISBN 3-550-07675-4]
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2010 Jürgen Köller
top |

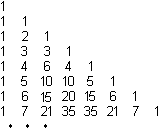 ...
...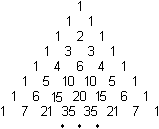 ...
... ....
.... ...
... ...
...


 ...
... ...
...
 ...
...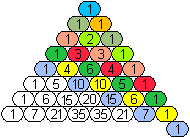 ...
...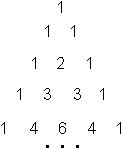 ...
...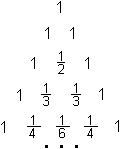
 ...
...