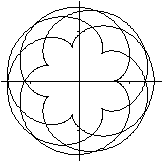
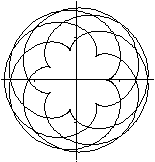
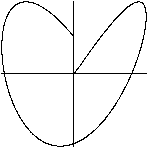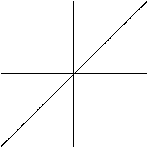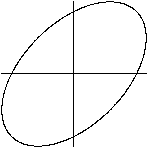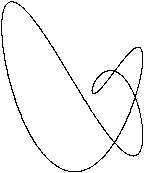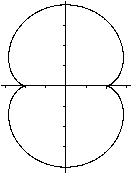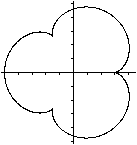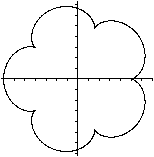|
Was ist eine Lissajous-Figur?
...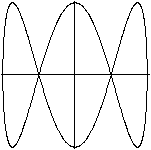 ...
x=sin(t) /\ y=sin(2t) ...
x=sin(t) /\ y=sin(2t)
|
Eine Lissajous-Figur ist der Graph, der durch die Parametergleichungen
x=a1sin(b1t+c1)
y=a2sin(b2t+c2)
beschrieben wird.
In Anlehnung an die harmonische Schwingung heißen
die Größen ai Amplituden,
bi Kreisfrequenzen und ci
Phasen (i=1, 2). |
Grundfiguren
top
Typische Lissajous-Figuren erhält
man über die vereinfachten Gleichungen
x=sin(b1t)
/\ y=sin(b2t).
Die Variablen b1
und b2 stehen für natürliche
Zahlen.
Beispiele
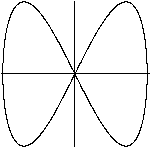
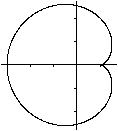
x=sin(t)
y=sin(2t)
|

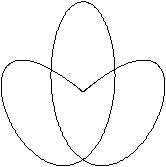
x=sin(t)
y=sin(3t)
|
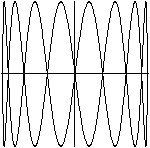
x=sin(t)
y=sin(8t)
|
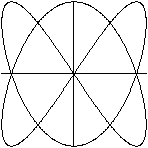
x=sin(2t)
y=sin(3t)
|
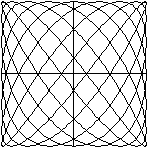
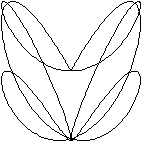
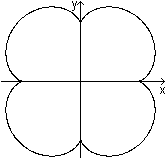
x=sin(7t)
y=sin(9t)
|
Beschreibung
der Grundfiguren top
Abgeschlossenheit
Es entstehen geschlossenen Kurven,
da die beteiligten Sinusfunktionen im Bereich {t | 0<= t<=2pi} periodisch
sind.
Symmetrie
... ... ... |
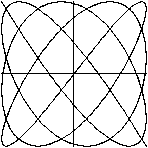
Alle Figuren haben die Darstellung x=sin(b1x)
/\ y=sin(b2x).
Die Figuren sind achsensymmetrisch bezüglich der
Achsen des Koordinatensystems,
denn es gilt sin(b1x)=sin[b1(-x)]
und sin(b2x)=sin[(b2(-x)]. |
Umschreibendes
Quadrat
...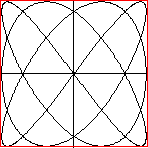 ... ... |
Die Figuren in einem Quadrat mit der Seitenlänge
2 Längeneinheiten, denn es gilt a1=
a2= 1. |
Berühr-Regel
... ... ... |
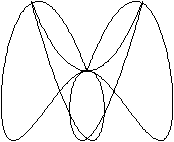
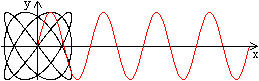
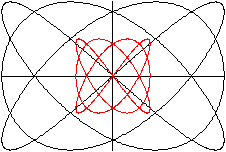
Der nebenstehende Graph berührt das umschreibende
Quadrat in der Vertikalen 3-mal und in der Horizontalen 4-mal.
Daraus kann man folgern, dass die Parametergleichungen
x=sin(3x) /\ y=sin(4x) sind.
Stellt man nämlich den Graphen zu y=sin(4x) im Intervall
von 0 bis 2pi dar, so erkennt man in seinen Scheitelpunkten die vier Berührpunkte.
Entsprechendes gilt für den Graphen zu y=sin(3x).
|
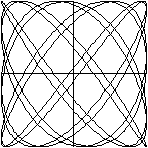
Verallgemeinerung
Figuren mit der Darstellung x=sin(b1x)
/\ y=sin(b2x) berühren das
umschreibende Quadrat in der Horizontalen b2-mal
und in der Vertikalen b1-mal.
Erweiterungen top
Phasenverschiebungen
Tritt zwischen den beiden Sinusfunktionen zu einer Grundfigur
eine "Phasenverschiebung" c1-c2
auf, so geht eine Symmetrie verloren. Die Graphen verändern sich je
nach Phasenlage, bewahren aber ihr Grundaussehen.
Das veranschaulichen die folgenden sechs Bilder.
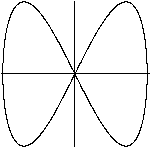
x=sin(t)
y=sin(2t)
|
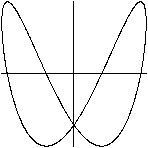
x=sin(t)
y=sin(2t+pi/5)
|
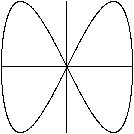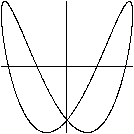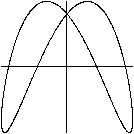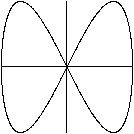
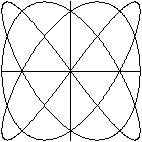
x=sin(t)
y=sin(2t+n*pi/10) (n=0, 1, 2, ..., 20)
|
Die Phasenverschiebungen sind pi/5 und in der Animation n*pi/10
(n=0, 1, 2, ..., 20)
x=sin(3t)
y=sin(4t)
|
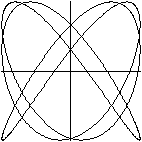
x=sin(3t)
y=sin(4t+9pi/10)
|
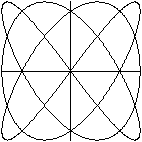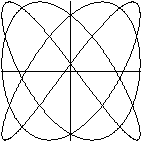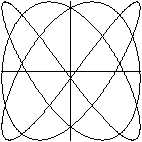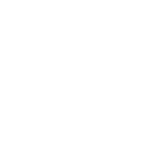
x=sin(3t)
y=sin(4t+n*pi/10) (n=0, 1, 2, ..., 20)
|
Die Phasenverschiebungen sind 9pi/10 und in der Animation
n*pi/10 (n=0, 1, 2, ..., 20)
Veränderung
der Amplituden
... ... ... |
Bisher galt für die Amplituden a1
= a2 = 1.
Wählt man z.B. a1
= 3 und a2 = 2, so wird die Lissajous-Figur
entsprechend gedehnt.
Die Parameterdarstellung ist x=3sin(3t) /\ y=2sin(4t). |
Bruchzahl
als Kreisfrequenz
... ... ... |
Bisher wurden nur natürliche Zahlen als Kreisfrequenzen
zugelassen.
So hat der nebenstehende Graph die Darstellung x=sin(7t)
/\ y=sin(9t)..............................................
|
... ...
x=sin(7/9t) ...
x=sin(7/9t)
y=sin(t)
|
In der Literatur kann man nachlesen, dass die Art der
Lissajous-Figur entscheidend durch das Verhältnis der Kreisfrequenzen
b1:b2
bestimmt wird.
Unter diesem Gesichtspunkt sollte man annehmen, dass die
Gleichungen x=sin(7/9t) /\ y=sin(t) zum gleichen Graphen führen.
(Übrigens muss man hier für t die Werte von 0 bis18pi einsetzen,
damit die vollständige Figur entsteht.)
Es sieht nicht so aus, als sei dieses der gleiche Graph.
Die Berühr-Regel gilt nicht. |
... ... ... |
Und das ist die Auflösung.
Man muss nur eine kleine Phasenverschiebung pi/5 einführen,
um einzusehen, dass es sich um eine Grenzform der Grundfigur oben handelt.
Es gilt
x=sin(7/9t+pi/5)
y=sin(t).........
0<=t<=18pi
|
Zwischenbemerkung
Durch die notwendige Erweiterung des Definitionsbereichs
von 0 bis 2pi auf 0 bis 18pi erreicht man, dass der Graph von x=sin(7/9t)
/\ y=sin(t) insgesamt 7 bzw. 9 Scheitel hat, die dann zu den Berührpunkten
im umfassenden Quadrat führen.
... ... ... |
Um die Grundfigur zu erhalten, muss man eine Phasenverschiebung
von pi/2 ansetzen.
Die Gleichungen heißen dann x=sin(7/9t-pi/2) und
y=sin(t) oder x=cos(7/9t) /\ y=sin(t).
Es bleibt 0<=t<=18pi. |
... ... ... |
Auch für die Parametergleichungen x=sin(t) /\ y=sin(9/7t)
mit 0<=t<=14pi ergibt sich der gleiche Ausartungsfall als Graph.
Es gilt hier 0<=t<=14pi.
Die Figur wird zur Grundfigur durch x=sin(t) /\ y=sin(9/7t-pi/2). |
Nicht
geschlossene Lissajous-Figuren top
Wie oben erwähnt, sind die Figuren nicht mehr geschlossen,
wenn mindestens eine Kreisfrequenz in den Parametergleichungen eine irrationale
Zahl ist.
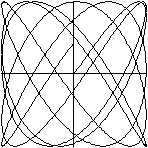
Das zeigt die folgende Bilderreihe für x=sin(t)
/\ y=sin(1.41421t). Die Dezimalzahl steht für sqrt(2).
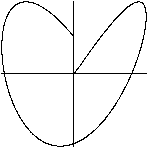
x=sin(t)
y=sin(1.41421t)
0<=t<=2pi
|
x=sin(t)
y=sin(1.41421t)
0<=t<=10pi
|

x=sin(t)
y=sin(1.41421t)
0<=t<=100pi
|

x=sin(t)
y=sin(1.41421t)
0<=t<=300pi
|
Es hat den Anschein, als fülle der Graph mit größer
werdendem Definitionsbereich immer mehr das umschreibende Quadrat aus.
Ausartungen top
Einige bekannte Graphen gehören zu den Lissajous-Figuren,
z.B. die Strecke, die Kreislinie,
die Ellipse und das Parabelstück.
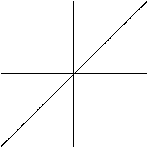
x=sin(t)
y=sin(t)
|

x=sin(t)
y=sin(t-pi/2)
|
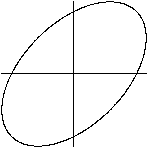
x=sin(t)
y=sin(t-pi/3)
|
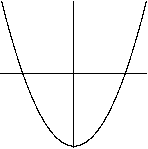
x=sin(t)
y=sin(2t+3pi/2)
|
|
Man kann die Aussagen über
ihre Koordinatengleichungen begründen.
Strecke
Die Gleichungen sind x=sin(t) /\ y=sin(t). Daraus folgt
y=x.
Kreis
Die Gleichungen sind x=sin(t) /\ y=sin(t-pi/2) oder x=sin(t)
und y=cos(t).
Aus sin²(t)+cos²(t)=1 folgt die Mittelpunktgleichung
des Einheitskreises
x²+y²=1.
Ellipse
Die Gleichungen sind x=sin(t) /\ y=sin(t-pi/3).
Es gilt nach dem Additionstheorem sin(t-pi/3)=sin(t)cos(pi/3)-cos(t)sin(pi/3).
Dann ist
y=(1/2)x-(1/2)sqrt(3)sqrt[1-sin²(t)]
<=> y=(1/2)x-(1/2)sqrt(3)sqrt(1-x²)
|*2
<=> (1/2)sqrt(3)sqrt(1-x²)=-y+(1/2)x
<=> sqrt(3)sqrt(1-x²)=-2y+x
|²
=> 3(1-x²)=4y²-4xy+x²
<=> 3-3x²=4y²-4xy+x²
<=> 4x²-4xy+4y²-3=0
Es gilt der Satz: Die Gleichung Ax²+Bxy+Cy²+Dx+Ey+F=0
stellt eine Ellipse dar, wenn 4AC-B²>0 ist.
Das ist hier der Fall: 4AC-B²=4*4*4-4²=48>0.
Parabel
Die Gleichungen sind x=sin(t) /\ y=sin(2t+3pi/2)
Es gilt nach dem Additionstheorem sin(2t+3pi/2)=-cos(2t)
und cos(2t)=1-2sin²(t).
Dann ist -y=1-2x² oder y=2x²-1. Das
ist die Gleichung der Parabel oben.
Verfremdung
der Parametergleichungen top
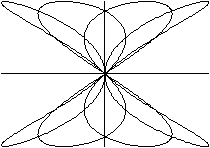
x=1.5sin(3t)sin(4t)
y=sin(4t)
|
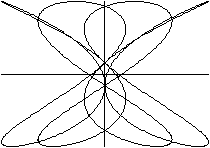
x=1.5sin(3t)sin(4t)
y=sin(4t+pi/20)
|
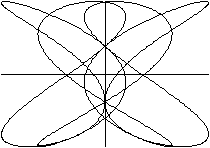
x=1.5sin(3t)sin(4t)
y=sin(4t+pi/8)
|
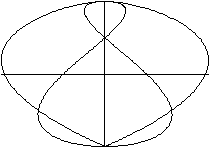
x=1.5sin(3t)sin(4t)
y=sin(4t+pi/2)
|
Die Figuren stehen auf dem Kopf.
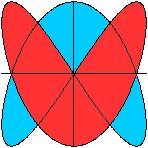
Einige Bilder dieser Seite
in Farbe
Epizykloiden
Über Epizykloiden, die auch durch Parametergleichungen
mit Sinusfunktionen beschrieben werden, gibt es an einer anderen Stelle
meiner Homepage eine
Seite.
Lissajous-Figur
im Internet
top
Deutsch
Wikipedia
Lissajous-Figur,
Harmonograph
Englisch
Eric W. Weisstein (MathWorld)
Lissajous
Curve
Famous Curves Index
Lissajous
Curves, Applet
Gerd Breitenbach
Vibrating
Strings, musical Intervals and Lissajous Curves
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Lissajous
curve,
Harmonograph
Xahlee
Lissajous
Französisch
Robert FERRÉOL, (Mathcurve)
COURBE
DE LISSAJOUS, COURBE
DE LISSAJOUS 3D
Referenzen top
(1) Heinz Nickel (u.a.): Algebra und Geometrie
für Ingenieur- und Fachschulen, Frankfurt/M Zürich 1966
(2) W. Gellert (Hrsg.): Kleine Enzyklopädie Mathematik,
Leipzig 1986
Feedback: Email-Adresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2011 Jürgen Köller
top |
 ...
...
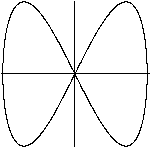



 ...
...

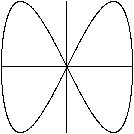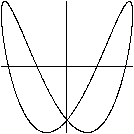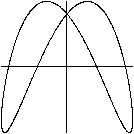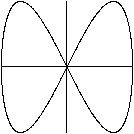



 ...
... ...
...
 ...
...