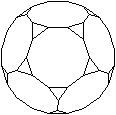
|
Was ist ein abgestumpftes Dodekaeder?
... ...
|
Ein abgestumpftes Dodekaeder ist
ein Körper, der von 12 regelmäßigen Zehnecken und 20 gleichseitigen
Dreiecken gebildet wird. |
Neben den 12+20=32 Seitenflächen hat das abgestumpfte
Dodekaeder 90 Kanten und 60 Eckpunkte.
Wer den 3D-Blick beherrscht,
sieht das abgestumpftes Ikosaeder räumlich.
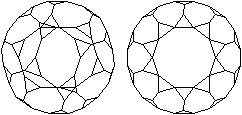
durchsichtig
|
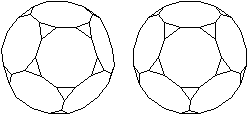
undurchsichtig
|
Entstehung
Es entsteht aus einem Pentagondodekaeder, indem man an
den Ecken passend dreiseitige Pyramiden abschneidet.
... ... |
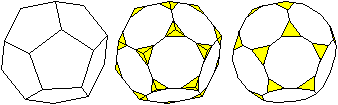Dazu teilt man alle Kanten so, dass regelmäßige
Zehnecke entstehen.
An den Ecken des Pentagondodekaeders entstehen gleichseitige
Dreiecke. |
Einordnung
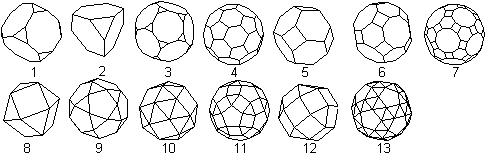Da beim abgestumpften Dodekaeder (3) an jeder Ecke regelmäßige
Vielecke in gleicher Weise aufeinandertreffen, gehört es zu den 13
archimedischen
Körpern.
Beschreibungen top
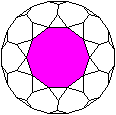
Umgebungen von Dreieck und Zehneck
... |
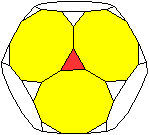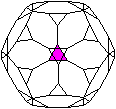
Jedes Dreieck ist von drei Zehnecken umgeben. |
... |
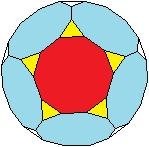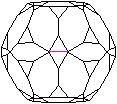
Jedes Zehneck ist von fünf Dreiecken und fünf
Zehnecken umgeben. |
Parallelprojektionen
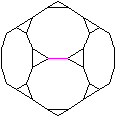
Ein Zehneck, ein Dreieck, eine
Kante und eine Kante liegen vorne.
Netz
|
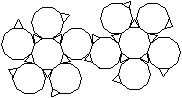
Ein Netz von vielen des abgestumpften Dodekaeders. |
Schlegel-Diagramm
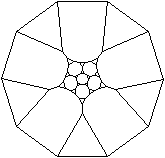
Diagonalen
420 Flächendiagonalen
... .... |
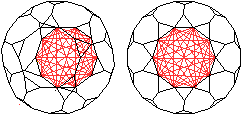Die Diagonalen der 10 Zehnecke bilden die Flächendiagonalen
des abgestumpften Dodekaeders. Jedes Zehneck hat 35 Diagonalen.
Das führt zu insgesamt 12*35=420 Flächendiagonalen. |
1260
Raumdiagonalen
... ... |
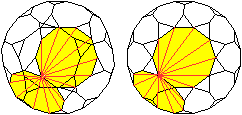Von jedem der 60 Eckpunkte gehen Verbindungslinien zu
den anderen Eckpunkten aus. Das sind 14 Flächendiagonalen und 3 Kanten,
wie die Zeichnung zeigt. In 60-17=43 Punkten enden dann Raumdiagonalen.
Das führt zu insgesamt (1/2)*60*42=1260 Raumdiagonalen
des abgestumpften Ikosaeders. |
Bilanz
Auf meiner Seite Dreieckszahlen
steht: "Verbindet man n Punkte mit allen möglichen geraden Linien,
so ergeben sich 1+2+3+...+(n-1)=(1/2)(n-1)n Strecken."
Für das abgestumpfte Ikosaeder bedeutet das, dass
es (1/2)*59*60=1770 Verbindungslinien gibt.
Das sind die 90 Kanten, 420 Flächendiagonalen und
1260 Raumdiagonalen.
Größen top
Das abgestumpfte Dodekaeder sei durch die Kantenlänge
a
gegeben.
Daraus lassen sich die weiteren Größen Radius
R
der Umkugel, Radius
rk der Umkugel, Volumen V
und Oberfläche O, Abstand
d3
der Dreiecke
und Abstand d10 der Zehnecke berechnen.
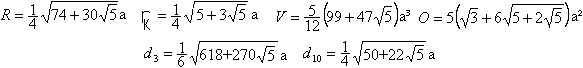
Herleitung der Formeln
Folgende Formeln werden u.a. in diesem Kapitel benutzt.
Gleichseitiges Dreieck:
Flächeninhalt A3 =
(1/4)sqrt(3)a², Höhe h = (1/2)sqrt(3)a
Zehneck:
Radius des Inkreises r10 = (1/2)sqrt[5+2sqrt(5)]a,
Radius des Umkreises R10 = (1/2)[sqrt(5)+1]a,
Flächeninhalt
A10 =
(5/2)sqrt[5+2sqrt(5)]a²; ferner cos(36°) = (1/4)[1+sqrt(5)]
Pentagondodekaeder:
V' = (1/4)[15+7sqrt(5)]a'³, Radius des Inkugel r'
= (1/20)sqrt[250+110sqrt(5)]a'
Radius des Inkugel R' = (1/4)[sqrt(3)+sqrt(15)]a'.
Vom
Fünfeck zum Zehneck
Zunächst einmal muss geklärt werden, wie man
vom Fünfeck des Dodekaeders zum Zehneck des abgestumpften Dodekaeders
gelangt.
... ...
|
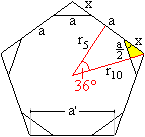
Genauer: Um welche Strecken x muss man die Fünfeckseiten
kürzen?
Die Strecke x taucht in einem gelben rechtwinkligen Dreieck
als Hypotenuse auf. Eine Kathete ist die halbe Seitenlänge des Zehnecks.
Der gekennzeichnete Winkel ist 36°, da seine Schenkel auf dem Mittelpunktwinkel
36° senkrecht stehen und der Winkel von 36° der halbe Winkel des
Grunddreiecks des Fünfecks ist. |
Es gilt cos(36°) = (a/2):x oder x = (a/2)/cos(36°).
Wegen cos(36°) = (1/4)[sqrt(5)+1] ist
x = (1/2)[sqrt(5)-1]a. Die Fünfeckseite ist a' =
2x+a = sqrt(5)a.
Oberfläche
Die Oberfläche setzt sich
aus den Flächeninhalten der 12 Zehnecke und der 20 Dreiecke zusammen.
Für das Zehneck gilt A10
=
(5/2)sqrt[5+2sqrt(5)]a², für das Dreieck A3 = (1/4)sqrt(3)a².
O = 12A10+20A3
=
12*(5/2)sqrt[5+2sqrt(5)]a²+20*(1/4)sqrt(3)a² = 5{sqrt(3)+6sqrt[5+2sqrt(5)]}a²,
wzbw.
Volumen
Man erhält das Volumen V des abgestumpften Dodekaeders,
indem man vom Volumen des Pentagondodekaeders 20x das Volumen der abzuschneidenden
dreiseitigen Pyramide subtrahiert.
... ... |
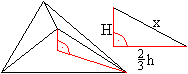Nach dem Satz des Pythagoras gilt H² = x²-[(2/3)h]²
oder
H² = {(1/2)[sqrt(5)-1]a}²-{(2/3)[(1/2)sqrt(3)]}²
=...
= (7/6)a²-(1/2)sqrt(5)a² = (1/6)[sqrt(7)-3sqrt(5)]a².
Dann ist H = sqrt(1/6){sqrt[sqrt(7)-3sqrt(5)]}a. |
|
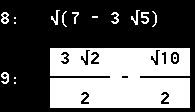
Darauf muss man erst einmal kommen:
sqrt[sqrt(7)-3sqrt(5)] = (1/2)[3sqrt(2)-sqrt(10)]
Derive half. |
Somit ist
H = sqrt(1/6)(1/2)[3sqrt(2)-sqrt(10)]a
= [sqrt(6)/12][3sqrt(2)-sqrt(10)]a
= [(1/12)[3sqrt(12)-sqrt(60)]a
= (1/12)[6sqrt(3)-2sqrt(15)]a
= (1/6)[3sqrt(3)-sqrt(15)]a
= (1/2)sqrt(3)-(1/6)sqrt(15)]a.
Das Volumen dieser Dreieckspyramide ist
V3 = (1/3)[1/4)sqrt(3)a²][(1/2)sqrt(3)-(1/6)sqrt(15)]a
= (1/24)[3-sqrt(5)]a³.
Das Volumen des Pentagondodekaeders ist V' = (1/4)[15+7sqrt(5)][5sqrt(5)]a³
= (5/4)[35+15sqrt(5)]a³.
Damit ist V = V'-20V3 = (5/4)[35+15sqrt(5)]-20(1/24)[3-sqrt(5)]
=...= (5/12)[99+47sqrt(5)], wzbw..
Radius
R der
Umkugel
... ...
|
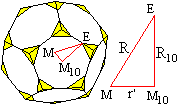
M ist der Mittelpunkt des Pentagondodekaeders.
In das abgestumpfte Dodekaeder legt man das rechtwinklige
Dreieck MM10E.
M ist der Mittelpunkt des Pentagondodekaeders, M10
ist der Mittelpunkt des Zehnecks. |
r' ist der Radius der Inkugel des Pentagondodekaeders, R10
ist der Radius des Umkreises des Zehnecks und R ist der gesuchte Radius
der Umkugel des abgestumpften Dodekaeders.
Nach dem Satz des Pythagoras ist R² = r'²+R10²
oder
R² = {(1/20)sqrt[250+110sqrt(5)]sqrt(5)a}²+{(1/2)[sqrt(5)+1]a}²
=
...
= (1/16){sqrt[74+30sqrt(5)]}a².
Dann ist R = (1/4){sqrt[74+30sqrt(5)]}a, wzbw..
Radius
rk der Kantenkugel
Bei archimedischen Körpern liegen die Kantenmitten
auf einer Kugel, der Kantenkugel.
... ... |
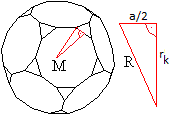Der Radius rk der Kantenkugel kann über
den Radius R der Umkugel bestimmt werden.
Im rechtwinkligen Dreieck gilt rk² =
R²-[(1/2)a]² = (1/16)[74+30sqrt(5)]a²-(4/16)a² = (1/4)[70+30sqrt(5)]a².
Dann ist rk= (1/4)sqrt[70+30sqrt(5)]a = (1/4)[5+3sqrt(5)]a,
wzbw. |
Abstand
d10
der
Zehnecke
Der Abstand der Zehnecke ist gleich dem Abstand der Fünfecke
des zugehörigen Pentagondodekaeders.
d10 = 2r' = (1/10)sqrt[250+110sqrt(5)]a' =
(1/2)sqrt[50+22sqrt(5)]a, wzbw.
Abstand
d3
der
Dreiecke
... ... |
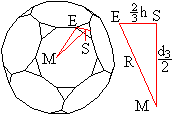Man erhält den halben Abstand der Dreiecke, wenn
man vom Radius R' der Umkugel des Pentagondodekaeders die Höhe H der
abzuschneidenden Pyramide abzieht.
(1/2)d3 = R'-H
|
Es gilt R' = (1/4)[sqrt(3)+sqrt(15)]a' = (1/4)[sqrt(3)+sqrt(15)]sqrt(5)a
= [(1/4)sqrt(15)+(5/4)sqrt(3)]a.
Für die Höhe H gilt H = [(1/2)sqrt(3)-(1/6)sqrt(15)]a
(s.o.).
Weiter ist d3/2
= R'-H = [(1/4)sqrt(15)+(5/4)sqrt(3)]a-[(1/2)sqrt(3)-(1/6)sqrt(15)]a =...
= (1/12)[5sqrt(15)+9sqrt(3)]a.
Dann ist d3 = (1/6)[9sqrt(3)+5sqrt(15)]a,
wzbw..
Zwei
Winkel
Der Winkel zwischen zwei Zehneckflächen ist 116°34'.
Der Winkel zwischen einer Dreieck- und Zehneckfläche
ist 142°37°.
(1)
Weitere Körper
top
Triakisikosaeder
... ... |
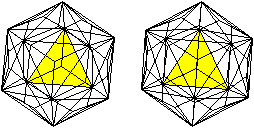Der duale Körper ist ein Ikosaeder mit auf die Seitenflächen
gesetzten, dreiseitigen Pyramiden. |
Ikosidodekaeder
... ... |
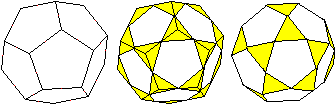Aus einem Pentagondodekaeder kann ein zweiter Körper
auch durch Abschneiden dreiseitiger Pyramiden entstehen. Dazu halbiert
man die Kanten.
Der Körper heißt Ikosidodekaeder. |
Abgestumpftes
Dodekaeder im Internet top
Deutsch
Wikipedia
Dodekaederstumpf,
Triakisikosaeder,
Archimedischer
Körper, Catalanischer
Körper
Englisch
Eric W. Weisstein (MathWorld)
Truncated
Dodecahedron, Archimedean
Solid, Triakis
Icosahedron
Geneviève Tulloue ( Figures Animées pour
la Physique )
Truncated
Dodecahedron and Icosidodecahedron (Applet)
G. Korthals Altes
Paper
Model Truncated Dodecahedron
Poly
A program
for downloading (Poly is a shareware program for exploring and constructing
polyhedra)
Die meisten Zeichnungen auf dieser Seite entstanden
mit Hilfe dieses Programmes.
Wikipedia
Truncated
dodecahedron, Triakis
icosahedron, Archimedean
solid, Catalan
solid
Französisch
Robert FERRÉOL
DODÉCAÈDRE
TRONQUÉ
Referenzen top
(1) H.Martyn Cundy and A.P.Rollett: Mathematical Models,
Oxford 1961 (Seite 109)
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© 2007,
überarbeitet 2013, Jürgen Köller
top |
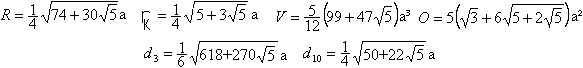
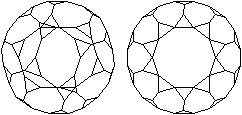
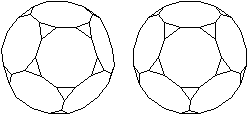
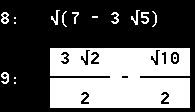
