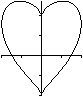|
What is the Heart Curve?

|
The heart curve is a closed curve, which has the shape
of a heart.
The heart is well known as a figure on playings cards
besides diamonds, cross and spades. |
If you speak about a heart, you rather mean the heart
figure than the heart shaped curve.
... ... ... |
In the simplest case, a heart is formed by a square standing
on its point and two semi-circles sitting on the sides. Characteristics
of the heart figure obviously are a groove above and a point below. |
... ... ... |
A heart figure develops also if you set two semi-circles
upon a triangle. But here you get two unpleasant corners.
Obviously you expect that these sides are rounded. |
... ... ...
|
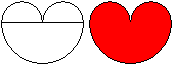
If the point below is missing then don't speak of a heart
but rather of a heart shaped figure. This form, however, is more
similar to the human heart.
The figure on the left is formed by three semi-circles. |
Drawn Heart Curves top
Method 1
...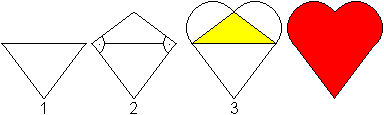 ... ...
|
1 Draw an isosceles triangle.
2 Draw the perpendiculars to the legs.
They produce a second isosceles triangle.
3 Draw two semi-circles upon the legs of the (now yellow)
triangle. |
Method
2
...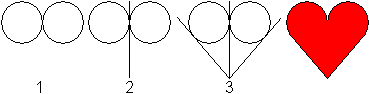 ... ...
|
1 Draw two touching equal circles.
2 Draw the common tangent.
3 Draw two further (outer) tangents from one point of
the tangent. |
Method
3
...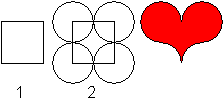 ... ... |
1 Draw a square.
2 Draw four equal circles. The centres are the corners
of the square and the common radius is "half square side". |
Method
4
...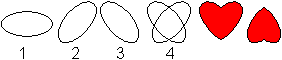 ... ...
|
1 Draw an ellipse.
2 Turn it about 45°.
3 Reflect it.
4 Form two hearts. |
Method
5
...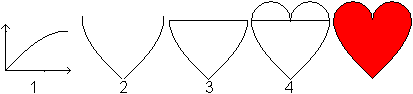 ... ... |
1 Draw the graph of f(x)=sin(x), 0<x<pi/2.
2 Turn the curve 90°. Reflect this curve.
3 Form a triangle of these two curves and a straight
line.
4 Set two semi-circles upon the triangle. |
Method
6
...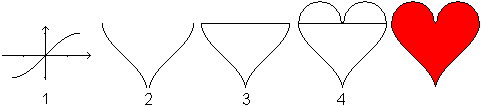 ... ... |
1 Draw the graph of f(x)=sin(x), -pi/2<x<pi/2.
2 Turn the curve 90°. Reflect this curve.
3 Form a triangle of these two curves and a straight
line.
4 Set two semi-circles upon the triangle. |
Calculated
Heart Curves top
It is a challenge to find formulas
which produce hearts.
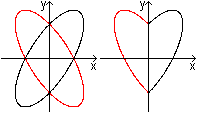
|
You can describe method 4 by formulas.
The black ellipse has the formula 2x²-2xy+y²-1=0.The
domain is {x| x>=0}.
The red ellipse has the formula 2x²+2xy+y²-1=0.
The domain is {x| x<=0}. |
You can leave out the domain, if you isolate y and use the
function f(x)=|x|.
Then y=|x|+sqrt(1-x²) and y=|x|-sqrt(1-x²)
describe a heart curve [(7)].
The formulas y=sqr(|x|)+sqrt(1-x²)
/\ y=sqrt(|x|)-sqrt(1-x²) are even better.
More curves
Sources:
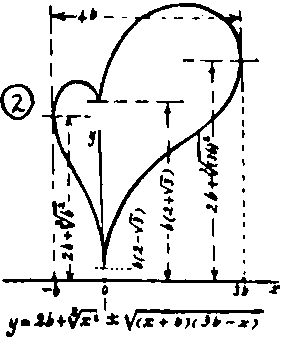
(Picture 1) Book 8, Eugen Beutel (1901) (2)
Buch 4, Aufgabe 8.5.5.,
(3) MathWorld (simplified formulas), (4)
H.-J. Caspar's web site (URL below), (6) Jurjen N.E.
Bos
From the desk of Torsten Sillke
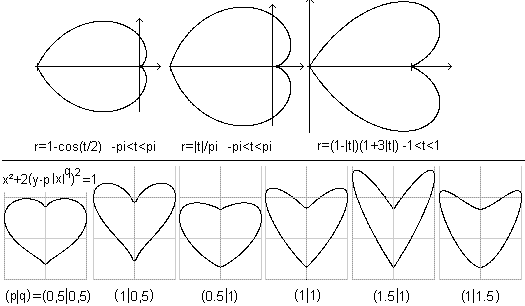
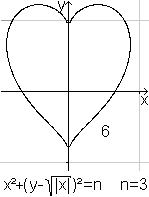
Threedimensional
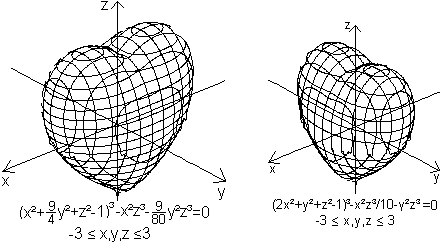
If you choose y=0 respectively x=0, you get the equation
of the 2D heart above on the left.
Source: Gabriel Taubin [for example MathWorld (URL
below)]
The graphs were made by the
freeware program "winplot" (Version 23.05.2000, URL below).
Winword Hearts top
And how do artists design a heart?
The heart appears as a well known figure in character
sets of programs under MS Windows. There it is a figure of playings
cards besides diamonds, cross and spades.
|
Here is a choice of well known character sets. |
The sets are Normaler Text, Arial, Courier New, Estrangelo
Edessa, Lucida Console, Symbol, Times New Roman, Webdings.
If you increase the letters from 12 to 72 you recognize
the shapes.

The originally black colour is replaced by the heart colour
red.
The upper part of the heart figure is formed by curves
similar to arcs. The lower lines do not approach linearly to the
point but usually are at first inward and then outward curved. That
gives the heart a special sweep.
Found at Unicode Standard,
Version 4.0
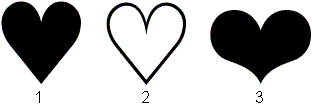
|
1 BLACK HEART SUIT 2665
2 WHITE HEART SUIT 2664
3 HEAVY BLACK HEART 2764 |
Pupils' Hearts top
And how do students draw a heart?
23 pupils of HS Lohfeld at Bad Salzuflen (Germany) were
to draw a simple heart.
The results are:

Thanks to Klasse 7a, Jg.2003/2004, about 12 years
old.
Heart Curve or Cardioid
top
How to produce it
... ... ... |
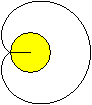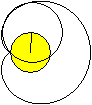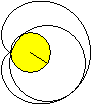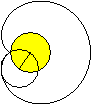
Draw a circle (on the left, yellow) and roll an equal
circle on it.
Fix one point on the moving circle line and follow this
point. It describes the heart curve or cardioid (on the right). |
...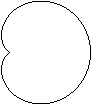 ... ... |
Another
way of producing a heart
... ... ... |
A cardioid can also be seen as the envelope of circles.
Draw a (yellow) circle and a fixed point P on the circle
line.
All circles that pass through the fixed point P and have
their centres on the (yellow) circle have a cardioid as an envelope. |
Area
and perimeter of the heart curve
Use the polar form r=2a[1+cos (t)] as the simplest
equation for calculating the area A and the perimeter U. The origin of
a coordinate system lies in the point of the cardioid.
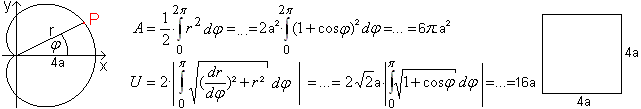
The perimeter is a rational number. A square with the
side 4a has the same one.
Mandelbrot
Set and Cardioid
...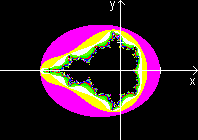 ... ... |
The "main figure" of the Mandelbrot set has the form
of the cardioid. The German name Apfelmännchen (apple man) uses this
shape.
Actually the main figure is a cardioid. The points
of the Mandelbrot set, which have convergent sequences, lie inside a cardioid.
Source: (5), page 208ff. There you find a proof and more
references. |
The picture was taken from my page Mandelbrot
Set.
Catacaustic
and Cardioid
... ... ... |
If light is falling on a spheric mirror (wedding ring
in the sun light), the reflecting rays form a special surface, the catacaustic.
It isn't a cardioid but a nephroid. A cardioid develops as an envelope,
if
the rays start at a point on the circle and are reflected at the circle
(drawing on the right). |
...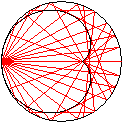 ... ... |
You find more on my German page Ringe.
Characteristic
Curve of a Microphone
...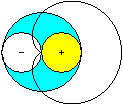 ... ... |
Microphones have a certain characteristic curve. In the
plane it is a circle for the "sound-pressure-receiver" and similar to a
lying eight figure for the "sound-velocity-receiver".
Special receivers like condenser microphones have both
capacities. Their characteristic curve develops by overlaying to a cardioid. |
Source: (6), page 550
The Broken Heart top
The broken heart (Das gebrochene Herz) is a tangram game.
...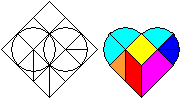 ... ... |
Lay inside a square two circles and draw some lines.
A heart develops, which is divided in nine pieces. The fun is to lay a
heart with the pieces or to discover new figures like those on the right. |
...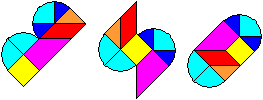 ... ... |
Source: (1) page 22, (2) page 140-145
The Woven Heart top
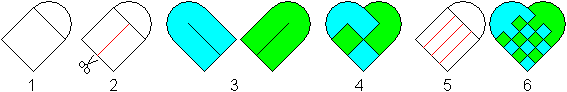
1 Draw a square and two half circles sitting on it.
2 Cut it in along the red line.
3 Copy it. Paint the paper in two different colours
or start with coloured paper.
4 Insert the blue piece in the green piece.
5,6 The heart works fine with a larger number of slits
as well.
... ... ...
|
If you like have a look at the heart
basket page made by Christopher Hamkins. |
Origami-Heart
top
... ... ... |
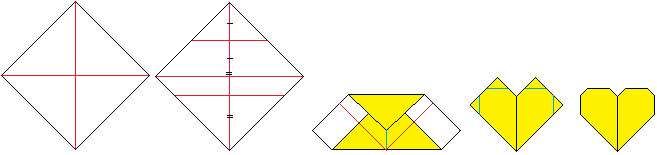 |
Tesselation of
Hearts top
...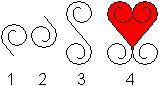 ... ... |
1 Give a spiral.
2 Reflect the spiral on the end point.
3 Connect both spirals to get a double spiral.
4 Reflect the double spiral. It forms a heart together
with the first double spiral.
Many hearts lead to a tesselation (on the right). |
...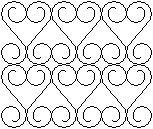 ... ... |
The idea for this drawing came from a window grill in Venice
(June 2004):

Venice is rich with heart
grills.

Rosettes of
Heart Figures
top
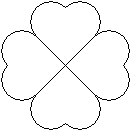
four-leaf clover
|

Once again a Venice photo- brightened up with some red.
|
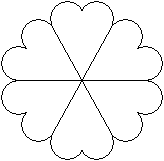
Six waffles
|

|
A pair of swans during the courtship display |
Photo on the web site fotocommunity (URL below)
Emoticons top
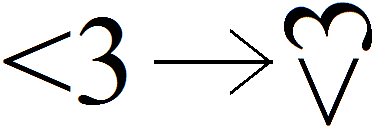

References top
(1) Pieter van Delft, Jack Botermans: Denkspiele der
Welt, München 1998 ISBN 3-88034-87-0]
(2) Karl-Heinz Koch: ...lege Spiele, Köln 1987 (dumont
taschenbuch1480) [ISBN 3-7701-2097-3]
(3) Heinz Nickel u.a: Algebra und Geometrie für Ingenieur-
und Fachschulen, Frankfurt / Zürich 1966
(4) Hans Schupp, Heinz Dabrock: Höhere Kurven,
BI Wissenschaftsverlag 1995 [ISBN 3-411-17221-5]
x^2 + 2( 3/5 (x^2)^(1/3) - y )^2
= 1
(5) Herbert Zeitler: Über die Hauptkörper spezieller
Funktionen, MNU, Jg.52, 1999, Heft4
(6) Bergmann-Schaefer: Lehrbuch der Expermentalphysik,
Berlin, NewYork 1975 [ISBN 3 11 004861 2]
(7) Norbert Herrmann: Mathematik ist überall, Oldenbourg
Verlag 2004 [ISBN 3-486-57583-X]
y = |x| +- sqrt(1 - x^2)
y = 2/3 ( (x^2 + |x| - 6)/(x^2
+ |x| + 2) +- sqrt(36 - x^2) ) (siehe auch Webseite von Thomas Jahre)
(8) Eugen Beutel: Algebraische Kurven, G.J. Göschen,
Leipzig 1909-11
(x^2 + y^2 - 1)^3 = 4x^2y^3
(9) Ulrich Graf: Kabarett der Mathematik, Dresden:
L. Ehlermann, 1942 Hardcover, 1.Auflage. (1943 Hardcover. 2. Auflage.)
(10) Michael Zettler: Und noch ein Herz. PM 6/99 Seite
274
y = sqrt(1 - (|x|-1)^2),
y = arccos(1 - |x|) - pi
(11) Thomas Hechinger: ... und noch ein weiteres
Herz. PM 2/00 Seite 67
y = sqrt(1 - (|x|-1)^2),
y = -3 sqrt(1 - sqrt(|x|/2))
(12) Mitteilung von Torsten Sillke:
x^2 + 2 (y - p*|x|^q)^2 = 1 (siehe
Schupp / Eisemann)
r = 2 sin^2(phi/4) = 1 - cos(phi/2)
mit |phi| <= pi (nach Eisemann)
r = |phi|/pi
mit |phi| <= pi. (Archimedische Spirale)
r = (1 - |phi|)(1 + 3|phi|)
mit |phi| <= 1. (nach Caspar)
(13) El-Milick, Elements d'Algebre
Ornementale, Paris, 1936:
y=(x)^(2/3)+(a²-x²)^(1/2)
und y=x^(2/3)-(a²-x²)^(1/2) and a=2
|
|
Heart Curves
on the Internet
top
German
33. Evangelischer Kirchentag in Dresden 2011
Google
Bilder
Armin Dietz
Das Herzsymbol
Christian Ucke und Christian Engelhardt
Kaustik
in der Kaffeetasse
[erschienen in: Physik in unserer Zeit, 29 (1998), Seite
120 bis 122]
Benutzer:Georg-Johann (Wikipedia)
Von
Punkt zu Punkt |
x(t)=12sin(t)-4sin(3t)
y(t)=13cos(t)-5cos(2t)-2cos(3t)-cos(4t) |
 |
luther.de
Die
Lutherrose
Fotocommunity
Frühlingsgefühle
(Thomas Th.)
Hans-Jürgen (Matroids Matheplanet)
Herzkurven
Hans-Jürgen Caspar
Kurven
x = a (-phi² + 40 phi +1200)
sin(pi*phi/180)
y = a (-phi² + 40 phi +1200)
cos(pi*phi/180)
Friedrich Krause
y = sqrt(|x|) +- sqrt(1 - x^2)
Michael Holzapfel
Herzkurve
aus zwei Funktionsteilen
y = sqrt(1 - (|x|-1)^2),
y = arccos(1 - |x|) - pi
(x^2 + y^2)(x^2 + y^2 - 2ax) -
a^2y^2 = 0 (Kardioide)
NN (Matheplanet)
Geometrie
in der Teetasse
Thomas Jahre (Chemnitzer Schulmodell)
Ein Herz für die Mathematik |
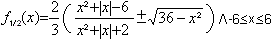 |
Torsten Sillke
Herzkurven
Wikipedia
Kardioide,
Herz
(Symbol), Herz
(Heraldik),
Herz
(Farbe)
English
Alex Bogomolny (Cut The Knot!)
Hearty
Munching on Cardioids
Eric W. Weisstein (MathWorld)
Circle
Catacaustic
graphicssoft.about.com
Four
Ways to 3D Hearts: Part 1
Jan Wassenaar
cardioid
JOC/EFR (School of Mathematics and Statistics, University
of St Andrews, Scotland)
Cardioid
Kurt Eisemann
x^2 + (y - 3/4 (x^2)^(1/3))^2 =
1 (Footnote)
r = sin^2( pi/8 - phi/4 ) (Footnote)
pacifict.com
Heart
(3D)
Pavel Boytchev
Mathematics
... loves you (Video)
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Cardioid,
Heart
(symbol)
Xah Lee
Cardioid
French
Robert FERRÉOL (mathcurve)
CARDIOIDE,
DOUBLE-COEUR
Japanese
Nobuo YAMAMOTO
Heart
Curves, Heart
Curves II, Heart
Curves IIb
Thanks to Torsten Sillke for several hints.
Gail from Oregon Coast - thank you for supporting me
in my translation.
Found on the Internet
;-):
the nerdy way of drawing a heart.
http://www.mathematische-basteleien.de/heart.htm
Must they do EVERYTHING in math? ><;; lol.
Feedback: Email address on my main page
This page is also available in German.
URL of my Homepage:
https://www.mathematische-basteleien.de/
©
Jürgen Köller 2004
top |
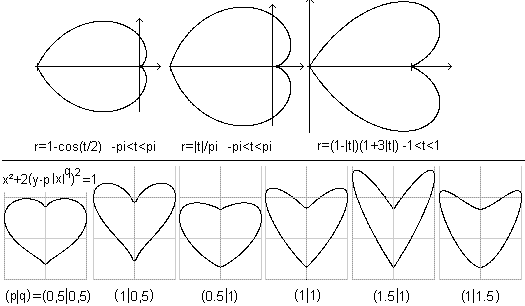
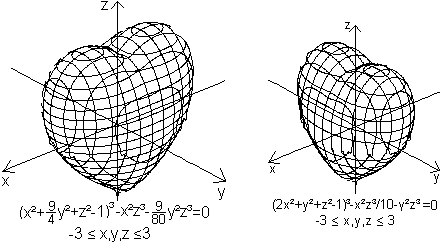


 ...
... ...
... ...
...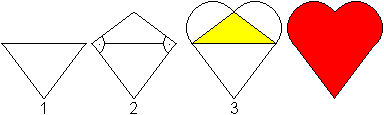 ...
...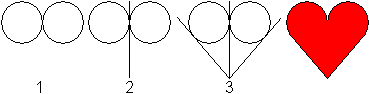 ...
... ...
...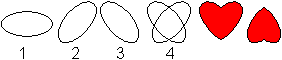 ...
... ...
... ...
...
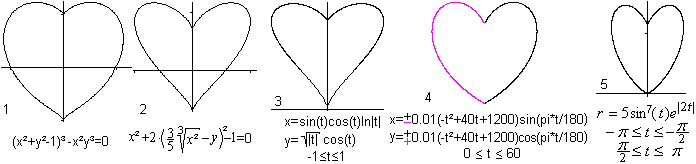

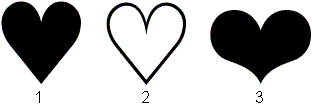
 ...
...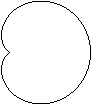 ...
... ...
...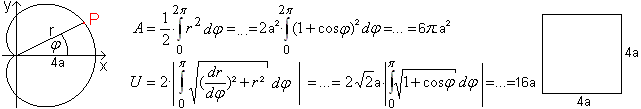
 ...
... ...
... ...
...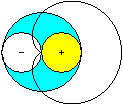 ...
...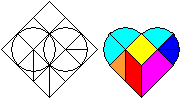 ...
...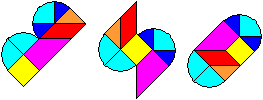 ...
...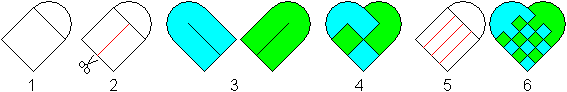
 ...
... ...
...
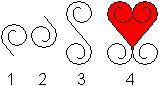 ...
... ...
...