|
Was ist ein Kreisring?
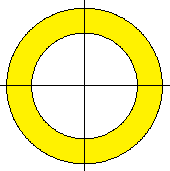 |
Ein Kreisring ist das Flächenstück zwischen
zwei verschiedenen Kreisen mit gleichem Mittelpunkt. |
Formeln
...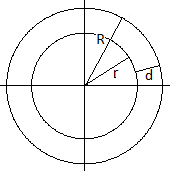 ... ... |
Ein Kreisring ist i.a. durch den inneren Radius r und
den äußeren Radius R bestimmt.
Dann hat er einen Flächeninhalt von A=pi(R²-r²).
Die Begrenzungslinien (Umfang) haben die Länge 2pi(R+r).
Sind die Breite oder Dicke d des Ringes und der innere
Radius r gegeben, so ist der äußere Radius R=r+d.
Für den Flächeninhalt gilt A=pi(2rd+d²).
Ist die Breite wesentlich kleiner als der Radius, so
gilt angenähert die vereinfachte Formel A=2pi*rd. |
Flächengleicher
Kreis
... ... ...
|
Der Kreis, der den gleichen Flächeninhalt wie der
Kreisring hat, hat einen Radius von x=sqrt(R²-r²).
Herleitung
Der gesuchte Kreis habe einen Radius von x.
Der Ansatz pi*x²=pi(R²-r²) führt
zu x=sqrt(R²-r²). |
... ... ...
|
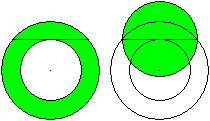
Man erhält den Durchmesser des flächengleichen
Kreises auch, wenn man an den inneren Kreis eine Tangente zeichnet und
den Abschnitt innerhalb des Kreisringes als Durchmesser des Kreises nimmt. |
Herleitung
...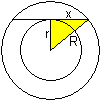 ... ...
|
Nach dem Satz des Pythagoras ist R²=x²+r²
oder x²=R²-r².
Für den Kreis mit dem Radius x gilt:
A=pi*x²=pi*(R²-r²). Das ist aber gerade
der Flächeninhalt des Kreisringes. |
Viele
konzentrische Kreise
Die unten stehende Figur ist als Zielscheibe bekannt.
...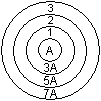 ... ... |
Sie besteht aus einer Folge von Kreisringen gleicher
Dicke. Die Radien der konzentrischen Kreise betragen r, 2r, 3r, 4r, ...
Für den inneren Kreis gilt A0=pi*r².
Für den ersten Ring gilt: A1=pi*[(2r)²-r²]=3*pi*r².
Für den zweiten Ring gilt: A2=pi*[(3r)²-(2r)²]=5*pi*r². |
Für den n-ten Ring gilt An=pi*[((n+1)r)²-(nr)²]=pi*(2n+1)r².
Kreisringe
aus In- und Umkreis
Zeichnet man zu den regelmäßigen Vielecken
die Um- und Inkreise, so entstehen Kreisringe.
Es folgen die ersten Vielecke und einige Daten.
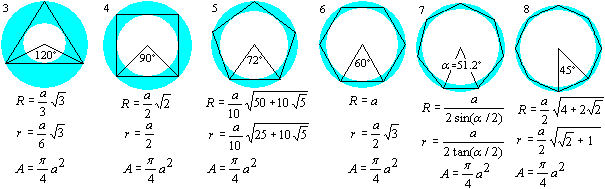
Es bedeuten
a: Seitenlänge eines Vielecks, R: Radius des Umkreises,
r: Radius des Inkreises, A: Flächeninhalt des Kreisringes.
Es ist erstaunlich, dass der Flächeninhalt aller
Kreisringe nur durch die Seitenlänge a des Vielecks bestimmt wird
und unabhängig von den Radien R und r ist.
Hohlzylinder top
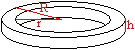
Der Hohlzylinder ist ein Körper, der von zwei konzentrischen
Zylindern gebildet wird.
... ... ...
|
Das Volumen des Hohlzylinders ist gleich V=pi*(R²-r²)*h.
Die Oberfläche setzt sich aus den Mänteln des inneren und des
äußeren Zylinders und den Kreisringen oben und unten zusammen:
O = 2*pi*R*h+2*pi*r*h+2*pi*(R²-r²) = 2*pi*(Rh+rh+R²-r²). |
Für einen Ring ist h<<r.
Ist d=R-r << h, so entsteht ein Rohr oder ein Schlauch.
- Sind h<<R und r<<R, so entsteht eine Scheibe.
Torus top
Der Torus heißt auch Ringkörper, Kreiswulst,
Rettungsring und in besonderen Ausführungen Kranz.
...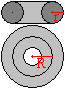 ... ... |
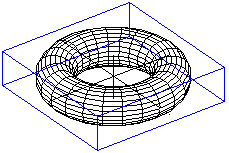
Ein Torus entsteht, wenn ein senkrecht stehender Kreis
um eine vertikale Achse außerhalb des Kreises rotiert. Kreis und
Achse liegen in einer Ebene.
Dabei ist r der Radius der Kreises und R der Abstand
der Kreismittelpunkte von der Drehachse.
Oben links zeigt sich der Torus im Schnitt, unten in der
Aufsicht. |
Man kann sich vorstellen, dass der Torus aus beliebig vielen
und beliebig dünnen Kreisscheiben besteht, die dann den Ring bilden.
Biegt man ihn zu einem Zylinder auf, so hat dieser die Grundfläche
pi*r² und die Höhe 2*pi*R.
Für das Volumen des Torus ergibt sich somit V =
(pi*r²)*(2*pi*R)=2pi²r²R.
Für die Oberfläche ergibt sich O=(2*pi*r)*(2*pi*R)=4pi²rR.
Das ist der Mantel des gedachten Zylinders.
Die exakte mathematische Herleitung dieser beiden Formeln
leisten die beiden Guldinschen Regeln.
|
Der nebenstehende Torus hat die Parameterdarstellung
x=cos(s)[3+cos(t)]
y=sin(s)[3+cos(t)]
z=sin(t)
mit 0<=s<2*Pi und 0<=t<2*Pi. |
Inzwischen (September 2010) hat der Torus
auf meiner Homepage eine eigene Webseite. Dort findet man mehr.
Verschlungene Ringe
top
Doppelring
... ... ... |
Zwei Ringe können so verbunden werden, dass man
sie nicht wieder trennen kann, ohne dass man einen Ring aufbricht. Diese
Anordnung von zwei Ringen gilt als ein Symbol der Treue und der Ehe. |
Mehrere so verbundene Ringe bilden eine Kette. Im Allgemeinen
ist sie in sich geschlossen wie z.B. bei der Halskette.
...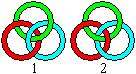 ... ... |
Drei Ringe kann man zu einem Dreieck verbinden. Auf den
ersten Blick sind die beiden Figuren gleich. Man stelle sich vor, man entferne
einen Ring, so bleiben links die Ringe verbunden, rechts sind die Ringe
dann einzeln.
Die rechte Anordnung heißt Borromäus-Verschlingung. |
Krupp-Ringe
...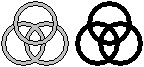 ... ... |
Bei einer Figur aus drei Ringen denkt man an die Kruppringe.
Sie weisen auf Alfred Krupps Erfindung des "nahtlos geschmiedeten und gewalzten
Eisenbahnradreifens" hin.
Die Ringe sind nicht ineinander verwoben. Der obere Ring
liegt vor den beiden unteren Ringen.
Heute werden die Ringe nicht mehr getrennt. (Mehr bei
Thyssen Krupp, URL unten) |
Audi-Ringe
... ... ...
|
Das Audi-Logo besteht aus einer geraden Kette von vier
Ringen.
Die vier Ringe stehen für die Marken Audi, DKW, Horch
und Wanderer, die 1932 zu der AUTO UNION zusammengefasst wurden. |
Die olympischen
Ringe
...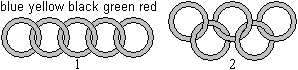 ... ... |
Jeder kennt das offizielle Emblem des IOK, die fünf
verschlungenen olympischen Ringe.
Sie entstehen dadurch, dass die gerade Kette (1) in W-Form
(2) gelegt wird. |
Die Farben der Ringe (und die Hintergrundfarbe weiß)
sind so gewählt, dass jedes Land eine ihrer Farben in den Olympischen
Farben wiederfindet.
Sie stehen offiziell nicht für die fünf Erdteile.
Trotzdem hat sich eine Zuordnung eingebürgert:
blau-Europa
gelb-Asien
schwarz-Afrika
grün-Australien
rot-Amerika
Es ist kein Zufall, dass ich die Ringe nicht gefärbt
habe. (Siehe Beitrag des Rechtsanwalts Thomas Engels, URL unten)
Trauring top
... ... ... |
Mathematisch gesehen ist der Trauring oder Ehering wie
der Torus ein Rotationskörper. Der Querschnitt ist aber kein Kreis,
sondern eine längliche Figur mit einer geraden Linie innen. |
Durch die gerade innere Begrenzung liegt der Ring besser
an, und es ist Platz für eine Gravur.
Es ist eine schöne Sitte, dass ein Ehepaar durch
das Tragen zweier gleicher Ringe auf dem Ringfinger die enge Verbundenheit
ausdrückt.
Stirbt der Ehemann, so trägt die Witwe beide Eheringe
nebeneinander.
Wir Deutschen tragen den Trauring am rechten Ringfinger.
Daran erkennt man uns im Ausland (auch).
Im Ring des Ehemannes steht meist der Vorname der Ehefrau,
umgekehrt steht sein Name in ihrem Ring.
Zusätzlich steht in beiden Ringen der Tag der Heirat.
Das ist eine Merkhilfe für Ehemänner ;-).
Es gibt zahlreiche Spiele oder Spielereien
mit Ringen. Hier eine kleine Auswahl.
Kreisel
... ... ... |
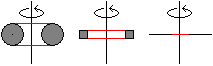
Der Trauring ist ein ausgezeichneter Kreisel.
Man fasst als Rechtshänder den Ring mit dem Zeigefinger
der rechten Hand und mit dem Daumen der linken Hand und gibt ihm ruckartig
zwei Drehmomente. Dabei müssen beim Loslassen beide Kräfte etwa
gleich groß sein, so dass er an einer Stelle bleibt und sich um die
vertikale Symmetrieachse dreht.
Der Ring dreht sich lange und so schnell, dass man eine
Kugel sieht. |
Katakaustik
... ... ... |
Legt man einen Trauring auf ein Blatt Papier und lässt
Licht von schräg oben auf ihn fallen, zum Beispiel das Sonnenlicht,
so wird es an der Innenwand des Ringes reflektiert. Die reflektierten Strahlen
leuchten das Innere etwas aus und überraschenderweise hat die Begrenzungslinie
zur Mitte hin die Form einer Drei. Das ist die Katakaustik. |
Das Zustandekommen der Katakaustik erklärt man am besten
durch eine Reihe von Zeichnungen.
 Man vereinfacht die Gegebenheiten zu einem ebenen Problem:
Aus der zylindrischen Innenfläche des Ringes wird ein Kreis.
Man vereinfacht die Gegebenheiten zu einem ebenen Problem:
Aus der zylindrischen Innenfläche des Ringes wird ein Kreis.
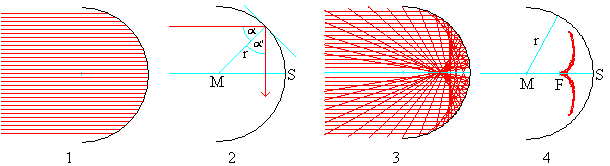
Bild 1: Von links fallen parallele Lichtstrahlen
in den Ring, der dann als sphärischer Spiegel wirkt. Wie werden sie
reflektiert?
Bild 2: Stellvertretend für die Parallelstrahlen
verfolgt man einen Lichtstrahl. Er wird an einer Stelle reflektiert, an
der ein "Spiegel" die Richtung der Tangentialebene hat. Das ist in der
Zeichnung die Tangente an den Kreis. Man findet sie, indem man die Senkrechte
zum Berührradius r zeichnet. Nach dem 1. Teil des Reflexionsgesetzes
liegen Lot (Radius), einfallender und reflektierter Strahl in einer Ebene.
Das ist hier die Zeichenebene. Nach dem 2.Teil des Reflexionsgesetzes ist
der Reflexionswinkel so groß wie der Einfallswinkel. Dadurch wird
der reflektierte Strahl gefunden.
Bild 3: Nach dieser Regel werden alle reflektierten
Strahlen eingezeichnet. Es ergibt sich Bild 3, das die Fotografie oben
gut wiedergibt.
Bild 4: Aus der Zeichnung lässt sich noch
mehr ablesen: Die Parallelstrahlen in der Nähe der Achse treffen sich
in einem (Brenn-)Punkt F. Die Brennweite f=FS ist gleich dem halben Kreisradius.
Pendeln
...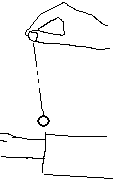 ... ... |
Mit einem Ring, der an einem dünnen Faden hängt,
kann man bei einer Frau feststellen, ob das nächste Kind ein Junge
oder ein Mädchen sein wird.
Das Pendel wird über das Handgelenk der Frau gehängt.
Der Ring selbst muss über dem Puls schweben (Bild). Hält
man die Hand oben still, so schwingt trotzdem das Pendel nach einer gewissen
Zeit. Schwingt es in einer Ebene hin und her, so kündigt sich ein
Junge an. Kreist der Ring, so kommt ein Mädchen.
Wer will, kann daran glauben ;-). |
Interessant ist eine Erklärung. Ich glaube, dass die
obere Hand nicht stillgehalten werden kann, schon weil das Herz rhythmisch
schlägt. Unbewusst erhält das Pendel Anstöße. Es ist
also wahrscheinlich ein Resonanzphänomen.
... ... ... |
Nebenbei: Das erinnert an einen alten Kinderspaß.
Man reißt im Frühjahr das Blatt eines Breitwegerichs so aus,
dass der Stängel (neue Rechtschreibung!) in der Mitte getrennt wird.
Dann hat der Blattstiel unten Fäden, die auf die spätere Kinderzahl
und durch unterschiedliche Längen auf den Abstand der Kinder untereinander
hinweisen. In diesem Fall werden drei Kinder kommen ;-). |
Ringraten
Ringraten ist ein altes Gesellschaftsspiel (siehe auch
Buch 1).
...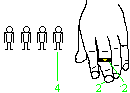 ... ... |
In einer Gesellschaft aus bis zu neun Personen steckt
sich eine Person unbemerkt von einem Außenstehenden, nennen wir ihn
A, einen Ring auf irgendein Fingerglied. Alle verbergen ihre Finger. Person
A muss herausfinden, wer den Ring trägt. Sie muss drei Zahlen nennen,
denn der Ort eines Ringes wird vorher durch drei Zahlen festgelegt: Das
sind die Nummer der Person (1 bis 9), die Nummer des Finger einer Person
(1 bis 4) und die Nummer des Fingergliedes eines Fingers (1 bis 3). |
A stellt der Gesellschaft eine Rechenaufgabe: Verdoppele
die Nummer der Person, addiere 5, multipliziere mit 5, addiere die Nummer
des Fingers, multipliziere mit 10, addiere die Nummer des Fingergliedes
und subtrahiere schließlich 250.
Zur Verblüffung der Gesellschaft nennt A den Ort.
Das ist das Resultat der Rechnung. Das ist eine dreistellige Zahl aus der
Nummer der Person, der Nummer des Fingers und der Nummer des Fingergliedes.
Rechnung:
[(2*4+5)*5+2]*10+2-250=422
Allgemein: Die Nummer der Person mit dem Ring sei a,
die Nummer des Fingers b und die Nummer des Fingergliedes c. Die Rechnung
lautet dann [(2*a+5)*5+b]*10+c-250 = 100*a+10*b+c.
Ringe aus Zahlen top
Bestimmt man die Dezimalzahl des Bruches 1/7 (zum
Beispiel durch schriftliches Dividieren von 1:7), so erhält
man die reinperiodische Darstellung 0,142857142857142857142857142857142857142857...
Diese Ziffernfolge kann man beliebig weit fortsetzen. Die Zahlen 142857
wiederholen sich und bilden die "Periode".
...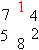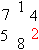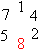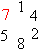 ... ... |
Es ist anschaulich, wenn man die Zahlen der Periode 142857
zu einem Kreis anordnet.
Es entsteht dann ein Ring, der immer wieder im Uhrzeigersinn
durchlaufen wird, wenn man die Genauigkeit der Dezimalzahl erhöht. |
Weiter gilt 2/7=0,285714..., 3/7=0,428571..., 4/7=0,571428...,
5/7=0,714285..., 6/7=857142.
Auch hier hat die Periode die Länge 6 und es tauchen
dieselben Ziffern auf. Man kann sogar den gleichen Ring wie bei 1/7 verwenden,
nur dass die Einsprungstellen in den Kreis unterschiedlich sind.
Statt 1/7 kann man auch 1/17 wählen. Die Periode,
als Zahl aufgefasst, heißt Phönixzahl. Es ist unentschieden,
ob es unendlich viele Phönixzahlen gibt (2, Seite 188).
(1) Torus (2) Hohlzylinder
(3) Kreisring
Ringe, Ringe, Ringe
top
Amulettring
Apfelpflücker
Armring, Armreifen
Benzolring
Bischofsring
Boxring ("Ring mit 4 Ecken")
Bullenring
"Der Ring schließt sich"
Dichtungsring
Einweckring
Fahrrad- oder Autoschlauch
Fresnelsche Ringlinse
Fußring
Halo
Halsring
Herr der Ringe
Hexenring
Hühnerring
Hoola Hoop
Iffland Ring
Iris des Auges
Jahresring
Kernspeicher
Kranz
Kreiswellen |
Magische Ringe
Meisenring
Mondring
Münze 1€ oder 2€
Nasenring
Ohrringe
Rauchring
RCDS (Ring christlich-demokratischer Studenten)
Reifen
Rettungsring
Ringbeschleuniger
Ringbuch
Ring der Nibelungen
Ring des Saturn
Ring, durch den ein Löwe springt
Ringe als Turngerät
Ringel
Ringelpiez mit Anfassen
Ringelreigen
Ringelschwänzchen
Ringelsöckchen
Ringe unter den Augen
Ringfahndung
Ringfinger
Ringgebirge |
Ringgraben
Ringleitung
Ringnebel
Ringmauer
Ringmuskel
Ringofen
Ringparabel
Ringraten
Ringsendung
Ringstraße
Ringstromeffekt
Ringtennis
Ringvorlesung
Ringwall
Schlüsselring
Schmuckring
Schwimmring
Siegelring
Token Ring
Trauring
Unterlegscheibe
Vogelberingung
Webring
Weißer Ring
Zauberring. |
Ringe im Internet top
Deutsch
Herwig Hauser (Fakultät für Mathematik, Universität
Wien)
Torus
animation
Homepage Gebrüder Grimm
Katakaustiken,
Vortrag von Dr. C. Ucke
Micha Peteler
Ring
schmieden
Rechtsanwalt Thomas Engels
Das
sprichwörtliche Spiel mit dem Feuer bei Verwendung der olympischen
Ringe
Thyssen Krupp
Firmenzeichen
Wikipedia
Kreisring,
Torus,
Ringkern,
Zylinder
(Geometrie), Olympische
Ringe, Borromäische
Ringe, Donut,
Phönixzahl
Englisch
Eric W. Weisstein (MathWorld)
Torus,
Double
Torus,
TripleTorus,
Impossible
Torus
Richard Parris (Freeware-Programme)
winplot
Wikipedia
Annulus
(mathematics),
Torus,
Toroid
(geometry), Cylinder
(geometry), Olympic
symbols, Borromean
rings, Doughnut,
Cyclic
number
Referenzen top
(1) Hans Nicklisch (Hrsg.): Schlag
nach, Natur, Leipzig 1952 (Seite 41/42)
(2) Endre Hódi (Hrsg.):
Mathematisches Mosaik, Köln
Ich bedanke mich bei Jürgen Dornieden für einen
klärenden Hinweis zu den Olympischen Ringen.
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2002, bearbeitet 2018, Jürgen Köller
top |



 ...
... ...
... ...
...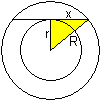 ...
... ...
...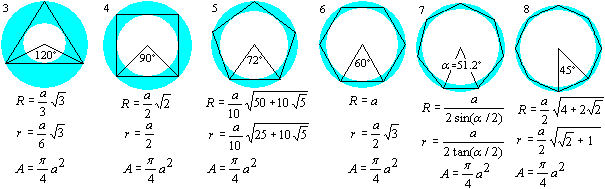
 ...
... ...
...
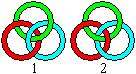 ...
...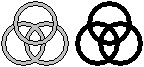 ...
...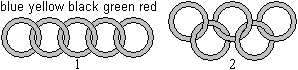 ...
... ...
... ...
... ...
... ...
... ...
...