What is the Mandelbrot Set?

.......

The black lying figure opposite is the Mandelbrot set called after its discoverer. In Germany we call it Apfelmännchen (apple-man) because of its shape. The illustration is in a coordinate system in the region  -3 < x < 2 and -2 < y < 2.  The computer graphics are formed by coloured points. The colours are derived from the coordinates (see more below).

The frayed edges of the Mandelbrot set are special. It is full of patterns. If you pick out a small box of the edges and calculate colours with the formula of the Mandelbrot set, you get different colourful patterns depending on the place.

......

You find this example at the box  - 0.37465401 < x < - 0,37332411 and  +0.659227668 < y < +0,66020767.

Mathematical Background top
(You can skip this chapter and go to First Contact to Winfract.) 
A short summary: To every point given by two coordinates you find a sequence and take a number from this sequence. This number is the code in a colour chart. The point gets this colour.

From Point to Sequence top
If you use complex numbers, the recurrence relation of the sequence is z_n+1=z_n² + c.
c=x₁ + y₁*i is the number which a colour has to be calculated for. 
z₀=0 is the start number.
The sequence is |z_n|. 

I choose the way with real numbers, because not many people are familiar with complex ones.

You use the following formulas for the Mandelbrot set.

x_n+1 = x_n²-y_n² + x₁ and y_n+1 = 2*x_n*y_n+ y₁ and a_n+1 = SQRT(x_n+1² + y_n+1²) with n = 0,1,2,3,... and the start values x₀=y₀=0. 
(SQRT = square root).

I explain the calculation with point P₁(x₁|y₁) = P₁(-0.40|0.70)  as an example.

I start with point N(0|0).
There is x₁ = x₀²-y₀² +x₁ = 0-0+x₁ = and y₁= 2*x₀*y₀ + y₁= 2*0*0+y₁= y₁, 
a₁ = SQRT(x₁² + y₁²) = SQRT[(-0.40)² + 0.70²] =0.81.

The first term a₁ is the distance of point P₁from the origin of the coordinate system.

The second term is derived from the coordinates of the given point P₁.
You calculate two new coordinates for a second point  P₂: 
x₂ = x₁²-y₁² +x₁ =  (-0.40)² - 0.70² + (-0.40) = -0.73 and   y₂= 2*x₁*y₁ + y₁= 2*0*0+y₁  = 2*(-0.40)*0.70+0.70 = 0.14. 
So you find  a₂ = SQRT(x₂² + y₂²) = SQRT[(-0.73)² + 0.14²] = 0.74.

The third term is derived from the coordinates of the previous point P₂ and the given point P₁.
You calculate two new coordinates for a third point P₃: 

x₃ = x₂²-y₂² +x₁  = (-0.73)² - 0.14² + (-0.40) = 0,11 and  y₃= 2*x₂*y₂ + y₁ = 2*(-0.73)*0.14+0.70 = 0.50. 
So you find  a₃ = SQRT(x₃² + y₃²) = SQRT(0.11² + 0.50²) = 0.51.

In this way you get the sequence 0.81, 0.74,  0.51,  1.0,  0.74,  1.1,  1.8,  2.4, ...  belonging to the given point P₁(-0.40|0.70). 

Five Points and their Sequences    top
The following chart shows the sequences of five points (examples) calculated by the same method.

. . Nr.  1 2 3 4 5 6 7 8 9 10 11 12 13 .

(0.20|0.20) 1st sequence 0.23 0,34 0.35 0.33 0.30 0.30 0.31 0.32 0.32 0.31 0.31 0.31 ... .

(0.10|0.65) 2nd sequence 0.66  0.84 0.44 0.57 0.91  0.83  0.38  0.70  1.0 0,77 0.83 1.3  2.1 ... .

(-0.40|0.70)  3rd sequence 0.81 0.74 0.51 1.0 0.74 1.1 1.8 2.4 4.9 24 560 320 000 ... .

(0.50|1.30) 4th sequence 1.4 2.8 6.5 43 1900  3 500 000 ... . . . . . . .

(2|2) 5th sequence 3.6 16  260  68 000 ... . . . . . . . . .

I rounded all numbers on 2 digits.

The first sequence is convergent with limit equal to 0.31. (The points with convergent sequences form the Mandelbrot set.) 

The other sequences are divergent. The terms get larger and larger without limits, but not in the same way. 

From the Sequence to the Colour     top
If a term of the sequence exceeds 2 in number (red), you can assume that the sequence gets larger and larger. This corresponds with the experience.
If you exceed 2, you write down the number of the previous term. It is the code of a colour chart.

I make a note of these numbers in tabular form: 

Point: Colour:

(0.2|0.2) black

(0.10|0.65) 12 (2)

(-0.40|0.70) 7

(0.50|1.30) 1

(2|2) 0

You give the colour black to the first point with the convergent sequence. So the Mandelbrot set becomes black.
Provided that you have a palette with 10 colours (0 to 9). If the number is larger than 9, you take the remainder of 10 (number mod 10). E.g. you take 2 instead of 12 in the second sequence.

Now the points can be drawn.

Computer in Action   top
The mathematical background up to now results in a huge material of numbers. You must calculate and analyse a sequence to every point. A computer can only do this. 

The computer cannot avoid one mistake: It cannot calculate all terms of a sequence. If it investigates only 50 terms for instance, maybe the sequence doesn't exceed 2 in number, nevertheless it is divergent. You make the mistakes less crass, if you determine more terms (e.g. 500). 

Nearly everyone who writes computer programs and is interested in computer graphics has had a try with the Mandelbrot set. It is an unforgettable experience if a simple program produces the complicated Mandelbrot set for the first time. In former times it took hours and hours (Commodore 64 nostalgia!).

Every own attempt of programming fades beside the standard program Fractint für Windows (Winfract), which has been developped by the "Stone Soup Group".

First Contact to Winfract top
If you want to occupy with the Mandelbrot set, you must really use this program.
I describe version 18.21. The program is freeware. Copyright: (c) 1990-1993 The Stone Soup Group.  It is available on the internet. 

After starting the program the Mandelbrot set appears. You form a small box with the mouse and move it with pressed mouse button to an edge. Then you press the enter key. A new picture appears on the screen. If you want you can look for a new place and press the enter key. The patterns repeat. You recognize self similarities.
 

.......

You often discover small, dark blue spots, which become Mandelbrot sets after magnification. Sometimes the "head" is crooked. Place:  0.435396403 < x < 0.451687191 0.367981352 < y < 0.380210061

You find a nice background picture for your computer at the place
-0.567709792 < x < -0.557685031 and 0.638956191 < y < 0.646482313
You set a palette in grey with Colors/Load Color Map.../altern.map .

If you save a picture, the coordinates of the boxes are also recorded. You find them with View/Status. 

You see the coordinates with View/Coordinate Box.

You can feed the coordinates into the computer via Fractals/Fractal Params...

You must choose Fractals/Reset all Options before looking for a new picture.
 

......

Often it is good to exceed the number of the terms of a sequence with Fractals/Basic Options and Maximum Iteration. You should choose 500 or 1000 terms instead of the set 150 ones (see above). The graphics show more details, as the animated gif on the left shows.

......

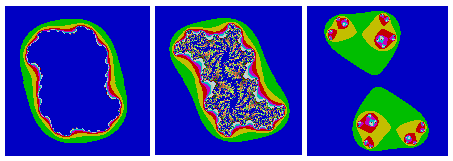
You find very nice pictures inside the three white boxes after magnification.

The program makes possible a trip through the fractal geometry beyond generating the Mandelbrot set. You must choose new formulas with Fractals/Formula... . 

Julia Sets     top
If you press the right mouse button being inside the program Winfract, you get symmetric Julia sets. You return to the Mandelbrot set if you press the button a second time. You always find a new Julia set to every point of the Mandelbrot set. 

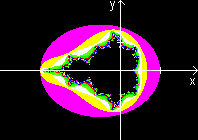
You see three Julia sets below. The pictures belong to the inside, the edges and the outside of the Mandelbrot set going from the left to the right. The picture in the middle shows fully detailed patterns with big depths. You calculate Julia sets with the same formulas as above, but with another handling. You give into xn+1 = xn²-yn² +x0' and yn+1 = 2xn*yn+y0' and an+1 = SQR(xn+1²+yn+1²) the coordinates of the point P(x0'|y0'), which you choose with the mouse button. You substitute the starting coordinates x0,y0  with the formula for the points. Those are the coordinates of the point, whose colour you want to calculate. 
You also come to Julia sets inside Winfract, if you choose Fractals/Formula... Julia. Now it is possible to give precisely two coordinates. You can't do it with the mouse button. 

Mandelbrot Set on the Internet  top

German

Albert Kluge
Das fraktale Apfelmännchen (Mandelbrot-Menge) als Java-Applet

Alexander F.Walz
Die Mandelbrotmenge

Bastian Bandlow
Komplexe Zahlen und Fraktale 

Christian Gloor 
Fractals mit 13 Bilder und einem Link auf Fractint, Download möglich 

Christian Symmank
Bilder der Mandelbrot Menge

Hanno Rein
Mandelbrot und Julia     Java Applet

Karsten Kremer
Zoom ins Apfelmännchen  (Apfelmännchen-Galerie, Theorische Grundlagen)

Klaus Rohwer
Fraktale, Fraktal-Galerie

Manfred Thole
Apfelmännchengalerie
Apfelmännchen, erzeugt in sechs Programmiersprachen:  Java-Code, PostScript-Code, TeX/LaTeX-Code, C-Code, Mathematica-Notebook, Macsyma-Code

Thomas Eigenheer
Generierung von Fraktalbildern der Mandelbrotmenge 2.1 (gratis)

Thomas Hövel
wincig (Fraktalprogramm,  Download)

Wikipedia
Mandelbrot-Menge

Eric W. Weisstein
Mandelbrot Set 

NN ("Fibonacci")
The Mandelbrot set  Applet

Wikipedia
Mandelbrot set

References    top
T.Wegener, M.Peterson, B.Tyler, P.Branderhorst: Fraktale Welten für Windows, München 1993
James Gleick: Chaos - die Ordnung des Universums, Knaur München 1988