Was ist der Goldene Schnitt?
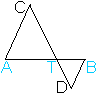
Man sagt auch: "Die Strecke AB wird durch T stetig geteilt" oder "Die Strecke AT ist die mittlere Proportionale zu AB und TB". Aus der Proportion AB:AT=AT:TB folgt die Produktgleichung AT²=AB*TB oder auch AT=sqrt(AB*TB). Dann ist auch die Deutung möglich: "Die Strecke AT ist das geometrische Mittel von AB und TB". Das Teilverhältnis Phi top
Die Proportion ist s:x=x:(s-x), die Produktgleichung s(s-x)=x². Das ist die quadratische Gleichung x²+sx-s²=0 mit den Lösungen x1=(1/2)[sqrt(5)-1]s und x2=(1/2)[-sqrt(5)-1]s. Es gilt x>0. Somit ist x=x1 die einzige Lösung. Es gibt also genau einen Teilpunkt. Das führt zum Verhältnis s/x=s/{(1/2)[sqrt(5)-1]}=(1/2)[sqrt(5)+1] oder gerundet s/x=1,618. Man bezeichnet dieses Verhältnis oft mit dem großen griechischen Buchstaben Phi. Das umgekehrte Verhältnis ist x/s=(1/2)[sqrt(5)-1] oder gerundet x/s=0,618. Es heißt dann konsequenterweise phi.
Schreibt man die Phi und phi als Dezimalzahlen, so habe die beiden Zahlen die gleichen Dezimalen: Die
stetige Teilung top
Die Teilung kann beliebig oft wiederholt werden.
Konstruktion
des Goldenen Schnitts top
 (2) Zeichne zu AB die Senkrechte durch B der Länge BC=(1/2)AB. (3) Zeichne die Strecke AC. (4) Zeichne einen Kreis um Punkt C mit dem Radius BC. Nenne den Schnittpunkt mit der Strecke Punkt S. (5) Zeichne einen Kreis um Punkt A mit dem Radius AS. Nenne den Schnittpunkt mit der Strecke AB Punkt T. Ergebnis: T teilt AB (innen) im Goldenen Schnitt. Beweis: Es sei AB=a. Es ist nach dem Satz des Pythagoras AC²=AB²+BC²=a²+[(1/2)a]²=(5/4)a². Dann ist AC=(1/2)sqrt(5)a. Für das gesuchte Verhältnis gilt AT:AB=AS:AB=(AC-CS):AB=[(sqrt(5)a-a]:2a=(1/2)[sqrt(5)-1] wzbw.. Äußere
Teilung top
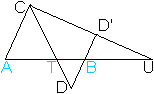
Diese Zeichnung wird erweitert.
Mit BD=BD' und zweimaliger Anwendung des 2.Strahlensatzes gilt AT:TB=AC:BD=AC:BD'=AU:UB. Man kann also in AT:TB den Punkt T durch Punkt U ersetzen. Ergebnis: Punkt T teilt Strecke AB innen, Punkt U die Strecke AB außen. Mehr findet man bei Wikipedia unter dem Stichwort "Harmonische Teilung" (URL unten). Darstellungen
von Phi und phi top
Die Zahl phi erfüllt die quadratische Gleichung x²+sx-s²=0 für s=1. Das heißt (phi)²+(phi)-1= 0. Die Zahl phi erfüllt also die quadratische Gleichung x²+x-1=0. Dann ist x(1+x)=1 oder x=1/(1+x). Für das rote x kann man wieder x=1/(1+x) setzen usw.. So entsteht der Kettenbruch. Die Zahl phi erfüllt die quadratische Gleichung x²+x-1=0. Die Zahl phi=1/Phi erfüllt die quadratische Gleichung x²+x-1=0 für s=1. Dann gilt (1/Phi)²+(1/Phi)-1= 0 oder 1+Phi-(Phi)²=0. Die Zahl Phi erfüllt also die quadratische Gleichung x²-x-1=0. Dann ist x²=x+1 oder x=sqrt(1+x). Für das rote x kann man wieder x=sqrt(1+x). setzen usw.. Das ist die Wurzelkette. Es gilt an+1/an=(an+an-1)/an.=1+an-1/an.=1+1/(an/an-1). Es sei qn die Folge der Quotienten. Dann gilt also qn =1+1/qn-1. Für den Grenzwert q bei n gegen Unendlich gilt analog q=1+1/q. Daraus folgt q²=1+q oder q²-q-1=0. Das ist aber die Bestimmungsgleichung für Phi. Das
goldene Dreieck und Rechteck top
Mehr über dieses goldene Dreieck und den Goldenen Schnitt findet man auf meinen Seiten Zehneck, Fünfeck, Doppelquadrat und Sterne.
Ausklang top
Im März 2008 besuchten wir Leipzig und bewunderten auch das historische Leipziger Rathaus. Es wurde 1556 unter dem regierenden Bürgermeister und Großkaufmann Hieronymus Lotter errichtet und gehört heute wohl zu den bedeutenden Bauten aus der Zeit der Renaissance. Der Turm teilt das Gebäude im Verhältnis des Goldenen Schnitts. Ich nehme an, es gibt entsprechende Baupläne, die das belegen. Es folgt zur Illustration eine Aufnahme dieses Rathauses, gesehen vom Dach des City-Hochhauses. Ich habe den Dachfirst rot gekennzeichnet und diese Linie nach dem Goldenen Schnitt geteilt.  Goldener Schnitt im Internet top Deutsch Joachim Mohr
Michael Holzapfel
Wikipedia
Englisch Eric W. Weisstein (MathWorld)
Jerzy Kocik
Wikipedia
URL meiner
Homepage:
© 2008 Jürgen Köller |
 ...
... ...
...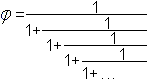
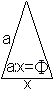 ...
...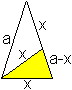
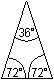 ...
...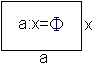 ...
... ...
...