What is a Flexagon?
A flexagon is a hexagon, which
you can make from a strip of triangles.
The point is: If you open the flexagon
in the middle, then a new face, which was hidden before appears.
How to
make a Trihexaflexagon
top
The simplest flexagon is a trihexaflexagon with three
faces.
(The colours in the drawings show you the front and the
reverse side.)
(1) Draw a strip of ten equilateral triangles with compasses
and ruler.
The length of a triangle is e.g. 4 cm. Then the strip
fits an A4 page.
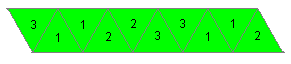(2) Number the triangles as given.
(3) Go over the lines with a ballpoint, so you can fold
the paper at the lines more easily later.
(4) Cut out the strip.
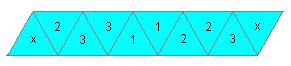(5) Turn the strip. Number the triangles as shown. Draw the
two crosses. x (left) is behind 3, 2 behind 1 and so on. Later the triangles
with a cross are glued on top of each other. Fold the paper several times,
so that the flexagon will be more flexible.
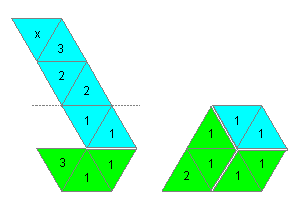(6) Fold the strip to form a hook. Then fold at the horizontal
line backwards. Notice that the front face has number 1 and the reverse
the number 2, therefore lay number 3 on 3.
(7) If you have succeeded in creating a hexagon, there
will also be a triangle jutting out from it. It must have a cross on the
reverse side. Glue both triangles with a cross to each other.
The flexagon is finished.
Flexagon turning left
... ... |
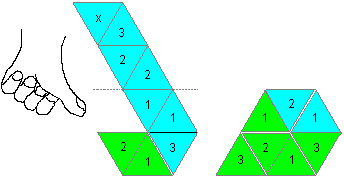You can also produce a trihexaflexagon, if you fold the
lower three triangles backwards and lay the four upper triangles forward
on the horizontal line. Glue the triangles 2 and 3 to each other. You call
this flexagon a flexagon turning left.
If the thumb of the left hand (drawing) points to the
strip, the fingers show you, which way to fold it. |
The flexagon above is called
right turning, because you must use the right hand now.
Right turning Flexagons are regular.
Flexing a Flexagon
top
 |
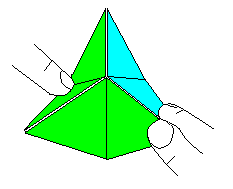It is difficult to open the flexagon for the first time.
Take hold of two triangles from the top with two fingers.
Move the triangles down. Push two triangles, which form a rhombus, at the
opposite corner with the index finger of your left hand down up to the
vertical 3D axis at the same time. Now you can open the hexagon like a
flower. The face number 3 appears.
This process is called "flexing". |
You can use two techniques to flex a flexagon continuously.
If you hold one diagonal of the hexagon horizontally
while flexing, you can open the flexagon on the left and on the right side
alternately. I call this way of flexing "swing".
There is another way of flexing continuously, called the
Tuckerman traverse. You flex, then you go to an adjacent corner, right
or left. - The results are the same.
The Trihexaflexagon
top
The trihexaflexagon has 9 segments of paper with triangles
on the front and reverse side. That makes 18 triangles in whole. The triangles
for gluing don't count.
The segments are not distributed regularly. Two lay on
another, between them is a single segment.
The trihexaflexagon has the distribution 1+2+1+2+1+2.
Two triangles of a face are joint together and form a
rhombus. The trihexaflexagon has 3 rhombi on each side.
While folding, the rhombus is folded back and appears
at the same place on the reverse side.
Folding further, the two triangles of the rhombus are
laid on one another. The triangles travel through 60 degrees.
.. ...... ... |
Fix a paper clip to one triangle. If you flex the
flexagon in the way of the swing, the paper clip and so the triangle is
moving anti-clockwise. The triangle with the paper clip is turned three
times at the same place before it is moved further though the flexagon
itself is not turned. |
You need 18 flexings for a full round.
If you write down the numbers of the faces appearing,
you have 1/2/3/1/2/3/1/2/3... The character "/" means that you have to
change the sides. If you turn the flexagon from the front to the rear side
you have the numbers 1/3/2/1/3/2/1/3/2...
The Tetrahexaflexagon
top
The tetrahexaflexagon has four faces and is a bit more
complicated than the trihexaflexagon.
|
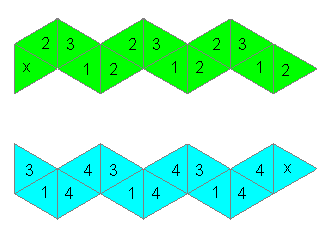
Make a strip from triangles as the picture shows. Number
the triangles on the front and on the reverse side as shown. First put
triangles 4 to 4 together. Then you have the strip of a trihexaflexagon.
Fold it in the same way as before. Glue the two triangles with a cross
after folding. |
If you flex the flexagon in the way of the swing, you get
the faces 1/3/2/1/3/2/1...
(You may have to turn the flexagon).
If you want to find face number 4, you have to keep opening
it on the left and on the right side as long as you can. E.g. you get the
sequence 1/34/1/32/1/34/1/32/... The numbers 1/34/1/32/ come back regularly.
In 1/34/1/32/ there are the numbers 1 and 3 twice, 2 and 4 once.
If you would like to show
the sequence in a diagram, you can make two.
|
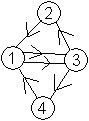
First you can draw a quadrilateral with two diagonals.
You can recognize the sequence 1/34/1/32/1/34/1/32/. |
|
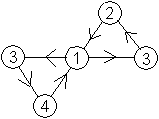
The second diagram shows two triangles with one
common point.
You can recognize the sequence 1/34/1/32/1/34/1/32/. |
The second (usual) diagram shows the different parts
of face 1 and face 3. In face 3 you are within a triangle, in face
1 you go through to the next triangle, if you like.
If you are following the
swing techniques, you go in the right diagram round the whole figure anti-clockwise.
You count the segments of the tetrahexaflexagon. The
segments, which have the faces 2,3 and 4, have the distribution 1+3+1+3+1+3.
Only the hexagon with the face 1 has the distribution 2+2+2+2+2+2. This
confirms the feature of a "through station".
You could think that face 1 is given priority. But if
you turn the flexagon from the front to the reverse side and flex, then
1 and 3 change their parts. So the symmetry is preserved.
Flexagon with a pattern
If you divide the equilateral triangles of the stripe in
three parts with the help of the centre point and colour them properly,
you get a trihexaflexagon with three nice patterns. The top and the reverse
side are the same in each case.
This version is developped by Krino Hoogestraat from
Emden.
Higher Flexagons top
There are expansions to 5,6,...faces, which are called
pentahexaflexagon, hexahexaflexagon,...
Pentahexaflexagon
|
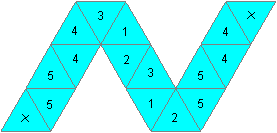
reflected horizontally:
|
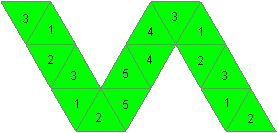
134/1/32/15/2/ :||
If you pile the number 5 triangles, you get the shape of
the tetrahexaflexagon with the same numbers. Go on like above.
Hexahexaflexagon
 .
1/236/2/315/3/124/ :||
If you pile the number 6 triangles, you get the shape of
the Pentahexaflexagon with the same numbers. Go on like above.
Hexahexaflexagon (Variation B)
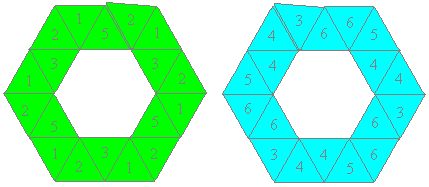
123/14/3/125/16/5/ :||
|
Hexahexaflexagon (Variation C)
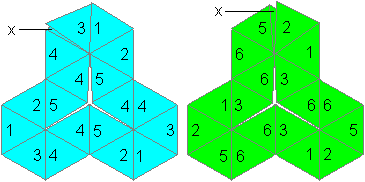
1256/2/51/23/14/3 :||
|
You find a detailed description
of this flexagon on my German page
Hexahexaflexagon.
Heptahexaflexagon
1367/3/61/324/3 :||
If you pile the number 7 triangles, you get the shape of
the Hexahexaflexagon with the same numbers. Go on like above.
Heptahexaflexagon
(Variation B)
1257/2/516/5/123/14/3/ :||
If you pile the number 7 triangles, you get the shape of
the Hexahexaflexagon (Variation B) with the same numbers.
Go on like above.
Tetraflexagons top
There are square shaped flexagons, too. I took the following
tritetraflexagon from Gardner's book from 1961, the tetratetraflexagon
from David Mitchell's recommendable book (4).
Tritetraflexagon
... ... |
Pile the squares 3 on 3, 2 on 2 and 1 on 1. Glue the
cross squares on each other. |
Tetratetraflexagon
... ... |
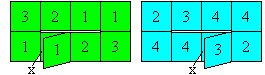Start now with 4 on 4, then take the following numbers.
The centre is cut along two squares, the cross squares
lie in the end. This is hidden in the drawing. |
Flexing
... ... |
You usually find new faces of the flexagons, if you turn
them and open them like a book in the middle. |
You can find more on my page tetraflexagons
and on my page Hexahexaflexagon (German
only).
Flexagons on
the Internet top
German
Claus Michael Ringel
Flexagone
Randolf Rehfeld
Flexagone
Wikipedia
Flexagon
English
Antonio Carlos M. de Queiroz
Hexaflexagons
Dave Richeson
Rubik’s
Cube Tri-Hexaflexagon
David King
Flexagons
Douglas C. George
Flexagon
Ela Schwartz
Flexagon
Fever
Eric W. Weisstein
Flexagon
Erik Demaine
Flexagon
Infinity12
Hexaflexagons
Jill Britton
Foto-TriHexaFlexagon
(THF) (Description of Fernando G. Sörensen's program, program
available)
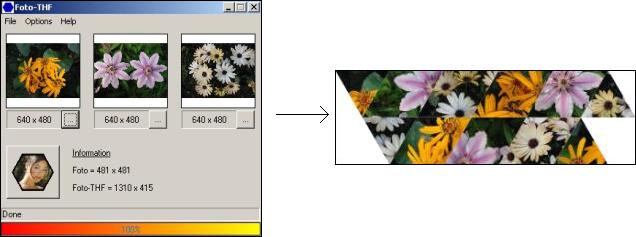
Program Foto-THF 1.2 (198Kb - fthf12.zip)
Choose "Opciones/Idioma/English (USA)"!
Kathryn Huxtable's
Flexagon
Page
Vi Hart (Khan Academy page)
Hexaflexagons
Kjartan Poskitt
The
Fabulous Flexagons
Les Pook
Flexagons
Martin Gardner
Hexaflexagons
Cambridge University Press, Martin Gardner’s First Book
of Mathematical Puzzles and Games (Excerpt)
Lee Stemkoski (Mathematrix)
Flexagons
NN
Flexifier
(Make your own tetra-tetraflexagon.)
Peter Bradshaw
Flexagon
Creator!
Robin Moseley
The Flexagon Portal
Scott Sherman
Flexagons |
Scott Sherman bietet viele Variationen von Flexagonen
aus Dreiecken an.
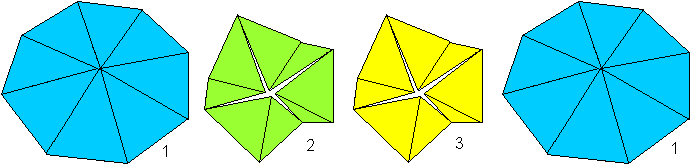
Dieses ist das "3 sided isosceles octaflexagon" (Tri-oktaflexagon)
als ein Beispiel.
Wenn man es in der Mitte öffnet, muss man wissen,
dass das Achteck in 2/3 der Stellungen nicht eben liegt. |
Wikipedia
Flexagon
www.g4g-com.org
Hexaflexagon
Youtube
Flexagon,
hexaflexagon-2
...
Yutaka Nishiyama
GENERAL
SOLUTION FOR MULTIPLE FOLDINGS OF HEXAFLEXAGONS (.pdf file)
References top
(1) Martin Gardner: Mathematical Puzzles & Diversions,
New York 1959
(2) Martin Gardner: The Second Scientific American Book
of Mathematical Puzzles & Diversions, New York 1961
(3) Martin Gardner: Mathematische Denkspiele, München
1987 (ISBN 3 88034 323 3)
(4) David Mitchell: The Magic of Flexagons, Norfolk England
1998 (ISBN 1 899618287)
(5) Les Pook: Flexagons Inside Out, Cambridge University
Press, 2003[ISBN 0 521 52574 8 paperback]
(6) Joseph S. Madachy: Madachy's Mathematical Recreations,
Dover Publications Inc., 1979
(7) Les Pook: Serious Fun with Flexagons, Springer-Verlag
GmbH, 2009 [ISBN-10: 9048125022]
My Comments top
Arthur H.Stone invented the flexagons in autumn 1939.
Flexagons became well known, when Martin Gardner introduced
them in the math corner of the magazine Scientific American
in the end of the 1950s.
The author looked back in his book (1) from 1959. He received
more than 100 letters.
Book 3 contains instructions for making a hexatetraflexagon.
It is surprising that the flexagons weren't known in Germany.
One reason probably was that book 1 was translated into German, but the
chapter about flexagons was left out.
It is no accident that I put flexagons at the first place
in my homepage.
I hardly don't know another mathematical puzzle of this
quality.
Do you know kaleidocycles?
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |