|
What are Triangular Numbers?
These are the first 100 triangular
numbers:
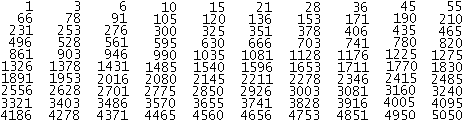
The sequence of the triangular numbers
comes from the natural numbers (and zero),
if you always add the next number:
1
1+2=3
(1+2)+3=6
(1+2+3)+4=10
(1+2+3+4)+5=15
...
You can illustrate the name triangular
number by the following drawing:
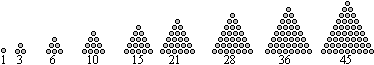
Formulas top
The general representation of a triangular
number is dn= 1 + 2 + 3 + 4 +...+ (n-2) + (n-1) + n,
where n is a natural number.
This sum is dn= n * (n
+ 1) / 2.
Proof:
dn= 1
+ 2 + 3 + ...+ (n-2) + (n-1) + n
dn= n
+ (n-1) + (n-2) +... + 3 + 2 + 1
------------------------------------------
Add both sides and combine the right terms in the pairs
(n+1). There are n terms.
2dn=n * (n+1)
dn= n * (n + 1) / 2, q.e.d.
There also is the recursion formula dn+1=
dn+ n with d1=1.
Special Triangular
Numbers top
Even and odd triangular numbers
... ... ... |
You see:
The even triangular numbers in red
and the odd numbers in black form pairs in the usual sequence. |
The smallest square numbers
1=1²
d8=36=6²
d49=1225=35²
d288=41616=204²
d1681=1413721=1198²
d9800=480024900=6930²
d57121=1631432881=40391²
...
|
The smallest palindromic numbers
d10=55
d11=66
d18==171
d34=595
d36=666
d77=3003
d109, d132, d173 , d363,
...
|
Perfect
numbers
A number which is equal to the
sum of all its divisors smaller than the number itself is called a perfect
number.
The first perfect numbers are 6,
28 and 496. They are triangular numbers like every perfect number.
The number
of 666
The sum of seven Roman numerals is D+C+L+X+V+I=666. The
letter M is missing.
You also can write: DCLXVI=666.
666 is the largest triangular
number which you can form of the same digits (1, page 98).
666 is a Smith number. This means:
The sum of digits [6+6+6] is equal to the sum of the digits of the prime
factors [2+3+3+(3+7)] (1, page 200).
The number 666 appears in an unfavourable
light, because it is called the "number of the animal" in the bible.
Here is wisdom! Who has good brains, should think
of the number of the animal; because it is a human's number, and this is
666 (John's revelation 13,18 in Luther's translation)
The number of the animal is a bad number in the interpretations
of the bible and is called the "number of the beast", "Satan's number",
or "Antichrist's number".
Consequently people looked in the names of the emperors
Nero and Diokletian for 666 and they found it, because they persecuted
the Christians. In the 16th century, in the time of the religious wars,
666 was connected with the name of Luther and on the other side with that
of the pope.
The example of the pope uses the idea of the chronogram:
The pope is called VICARIUS FILII DEI (deputy of God). If you add the values
of the Roman numerals, you get 666 (VICARIVS FILII DEI).
You are flooded with information on the internet by searching
with 666, if you like.
Counting Pairs top
You give eight squares with the numbers 0,1,2,3,4,5 and
6. They are arranged to pairs.
 There are 7+6+5++4+3+2+1=28 pieces. This is a triangular
number.
There are 7+6+5++4+3+2+1=28 pieces. This is a triangular
number.
... ... ...
|
There also are dominoes with 36 or 45 pieces, if you
add the squares with 7 and 8 numbers. |
Everybody
with each other
...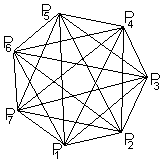 ... ...
|
If you join n points as often as possible, you get 1+2+3+...+(n-1)
lines.
An example with n=7 on the left. |
Shaking hands
Everybody shakes hands with each other. Result: You shake
hands (1+2+3+...+(n-1)) times.
Prost
Everybody clinks glasses of champagne with each other.
Numbers
of recangles inside a nxn square top
... ... ...
|
There are 36 rectangles inside a 3x3 square, 14 of them
are squared. |
Derivation for a n*n square:
Every rectangle is formed by pairs of vertical and horizontal
lines.
There are n+1vertikal lines. You can arrange them to
n(n+1)/2 pairs. n+1 horizontal lines also have n(n+1)/2 pairs.
There are [n(n+1)/2]² combinations alltogether.
If you give n=3, you get 36.
You can easily generalize to the numbers of rectangular
solids inside a cube and even inside a rectangular solid.
Gauss Sum top
There is a story about the famous mathematician Karl
Friedrich Gauß (1777-1855), when he was a child. He should add the
numbers 1 to 100. The teacher thought, that he would be busy with it for
a long time. But Karl Friedrich found the sum 5050 after some minutes.
Instead of adding the numbers one after the other, he made pairs of numbers
and could multiply:
1+2+3+4+...+50+51+...+97+98+99+100
= (1+100) + (2+99) + ... + (50+51)
= 50*101
= 5050.
[(3), page 22f.]

Position
in Pascal's Triangle top
...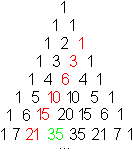 ... ...
|
Pascal's triangle makes a contribution to many fields
of the number theory.
The red numbers are triangle numbers.
You even can find the sum of the triangular numbers easily.
Example: 1+3+6+10+15=35 |
You can express the triangular numbers as binomial coefficients

Figurate Numbers
top
You can generalize the triangular
numbers and go further to quadrilateral, pentagons, ...
triangular numbers
square numbers
pentagonal numbers
hexagonal numbers
heptagonal numbers
octogonal numbers
...
|
n*(n+1)/2
n²
n*(3n-1)/2
n*(4n-2)/2
n*(5n-3)/2
n*(3n-2)
...
|
1 3 6 10 15 21 28...
1 4 9 16 25 36 49...
1 5 12 22 35 51 70...
1 6 15 28 45 66 91...
1 7 18 34 55 81 112...
1 8 21 40 65 96 133...
...
|
It is fun to find out which triangular numbers also appear
in the new sequences.
You can generalize from 2d- (triangle numbers)
to higher dimensions:
triangular numbers
tetrahedral numbers
hypertetrahedral numbers
...
|
n*(n+1)/2
n*(n+1)*(n+2)/6
n*(n+1)*(n+2)*(n+3)/24
...
|
1 3 6 10 15 21...
1 4 10 20 35 56...
1 5 15 35 70 126...
...
|
Here you also have the question, which triangular numbers
repeat in the new sequences.
There is the famous theorem:
The sum of two successive numbers is a square number.
Proof: Add dn and dn+1. The result
is (n+1)². See also the drawings with the triangles above.
Triangular
Numbers on the Internet top
German
blogger.de
153
Jutta Gut
Figurierte
Zahlen - die Arithmetik der Spielsteinchen
Wikipedia
Dreieckszahl,
Zentrierte
Dreieckszahl, Polygonalzahl,
Sechshundertsechsundsechzig,
Hundertdreiundfünfzig,
Gaußsche
Summenformel
English
Alexander Bogomolny (cut-the-knot)
There
exist triangular numbers that are also square
Bit-Player
Versions
of the Gauss Schoolroom Anecdote
Eric W. Weisstein (MathWorld)
Triangular
Number, Figurate
Number, Heptagonal
Triangular Number, Octagonal
Triangular Number,
Pentagonal
Triangular Number, Pronic
Number, Square
Triangular Number
Mathpages.com
Square
Triangular Numbers
Patrick De Geest (World of Numbers)
Palindromic
Triangulars
Peter Macinnis
Enquiring
into triangular numbers
Shyam Sunder Gupta
Fascinating
Triangular Numbers
Wikipedia
Triangular
number, Centered
triangular number, Polygonal
number, 153
(number), 666
(number)
References top
(1) Martin Gardner: Die magischen Zahlen des Dr. Matrix,
Frankfurt
am Main 1987 [ISBN 3-8105-0713-X]
(2) Jan Gullberg: Mathematics - From the Birth of Numbers,
New York / London (1997) [ISBN 0-393-04002-X]
(3) Walter Lietzmann: Lustiges und Merkwürdiges
von Zahlen und Formen, Göttingen 1969
Thank you Gail from Oregon Coast for supporting me
in my translation
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
2004 Jürgen Köller
top |
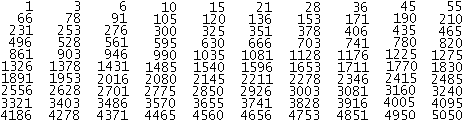
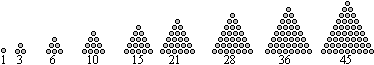


 ...
... ...
...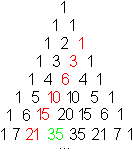 ...
...