Regelmäßiges 30-Eck

Inhalt dieser Seite

Was ist das regelmäßige 30-Eck?
Diagonalen
Vielecke aus Diagonalen

Zur Hauptseite "Mathematische Basteleien"

Was ist das regelmäßige 30-Eck?

...... Das regelmäßige 30-Eck ist ein Vieleck mit
30 gleich langen Seiten,
30 gleich großen Innenwinkeln.
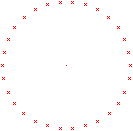
In der nebenstehenden Zeichnung werden nur die Eckpunkte des 30-Ecks gezeichnet.
Ansonsten könnte man das 30-Eck kaum von einer Kreislinie unterscheiden.

...

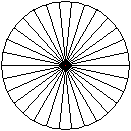
Man kann das 30-Eck durch einen Kreis und 30 kongruente Kreisausschnitte darstellen.

Das 30-Eck ist an sich nichts Besonderes.
Ich habe es gewählt, weil 30 viele Teiler hat. Das 30-Eck enthält somit interessante Vielecke.
Es wird sich herausstellen, dass hier eine schöne Anwendung des "größten gemeinsamen Teilers" vorliegt.

Diagonalen top
Das 30-Eck hat n(n-3)/2=30(30-3)/2=405 Diagonalen.

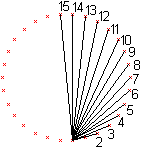...... Es gibt aber nur (n-2)/2=(30-2)/2=14 Diagonalen, die voneinander verschieden sind. Sie werden links in der üblichen Nummerierung der Diagonalen im Vieleck dargestellt.
Die Diagonalen heißen d₂ bis d₁₅.
Diese Aussagen beziehen sich auf Formeln der Webseite Regelmäßige Vielecke.

Vielecke aus Diagonalen top
Die Diagonalen einer Länge werden herausgegriffen. Man kann sie in drei Klassen aufteilen.
1 Klasse: Sechs Diagonalen und regelmäßige Vielecke

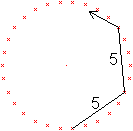...... Als erstes wird die Diagonale d₅ betrachtet.
5 ist ein echter Teiler von 30. So wird schon nach einem Umlauf der Startpunkt wieder erreicht.
Man muss d₅ sechsmal hintereinander hängen. Das führt zum regelmäßigen Sechseck.

Die anderen echten Teiler von 30 sind 2, 3, 6, 10, 15.
Sie führen zum 15-Eck, Zehneck, Fünfeck und Dreieck.
Zum Teiler 15 gibt es kein Vieleck, d₁₅ ist der Durchmesser des Umkreises.

2.Klasse: Drei Diagonalen und 30-zackiger Stern
Das nächste Beispiel ist die Diagonale d₇.

...

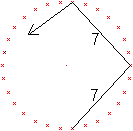7 und 30 haben keinen gemeinsamen Teiler. Sie sind teilerfremd.
Hier braucht man 30 Strecken, um wieder zum Startpunkt zu gelangen. Das kleinste Vielfache von 7, das gleichzeitig Vielfaches von 30 ist, ist 7*30=210. Es entsteht ein 30zackiger Stern.
Die anderen Zahlen dieser Art sind 11 und 13.

3.Klasse: Fünf Diagonalen und Sterne mit einer Zackenzahl kleiner als 30
Das nächste Beispiel ist die Diagonale d₄.

...

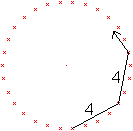4 und 30 haben den kleinsten gemeinsamen Teiler 2, [ggT(30,2)=2].

Also braucht man 2 Umläufe, um wieder am Startpunkt anzukommen. Man erhält ein 15-Eck.

Neben 4 gibt es weitere Zahlen, die mit 30 einen echten gemeinsamen Teiler haben. Das sind die Zahlen 8, 9 12 und 14.
ggT(30,8)=2 führt auch zum 15-Eck, ggT(30,9)=3 zum Zehneck, ggT(30,12)=6 zum Fünfeck, ggT(30,14)=2 zum 15-Eck.

Auch die Figuren der 1. und der 2. Klasse kann man wie die der 3. Klasse durch das ggT kennzeichnen:
Für die 1. Klasse gilt ggT(Teiler von 30|30)=Teiler von 30 und für die 2. Klasse ggT=1.

Liste der Vielecke top
Alle Möglichkeiten werden in einer Tabelle zusammengestellt.
Die Variable i sei die Nummer der Diagonalen, n die Anzahl der Ecken der Vielecke und s die Anzahl der regelmäßigen Sterne

i
ggT(30,i)
n-Eck [n=30/ggT(30,i)]
s 2
2
15
1 3
3
10
1 4
2
15
2 5
5
6
1 6
6
5
1 7
1
30
1 8
2
15
2 9
3
10
3 10
10
3
1 11
1
30
1 12
6
5
6 13
1
30
1 14
2
15
2

In der letzen Zeile wird erfasst, wie viele Sterne man jeweils erzeugen kann. Ist das Vieleck regelmäßig, kann man einen Stern erzeugen, indem man es dreht. Zum Beispiel dreht man für i=6 das Fünfeck fünfmal und erhält einen 30zackigen Stern.
In einem 30-Eck stecken also immerhin 23 Sterne. Das ist die Summe der Zahlen der letzten Zeile.

Zum Schluss noch zu jeder Diagonalen eine Figur:

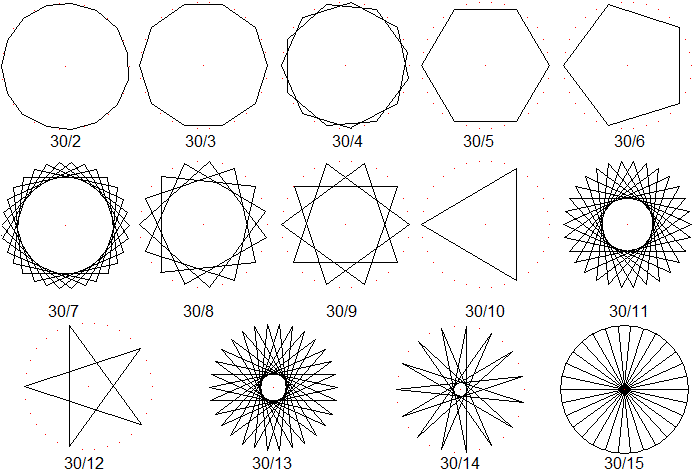
Siehe auch: Eric W. Weisstein (MathWorld) Star Polygon

Die Zahl 30 top
Die Zahl 30 hat weitere Besonderheiten.
>30 ist das Produkt der drei kleinsten Primzahlen 2,3 und 5.
> 30 ist eine quadratische Pyramidalzahl.
>Das Ikosaeder und das Pentagondodekaeder haben 30 Kanten, das Ikosidodekaeder 30 Ecken.
>In Lehrbüchern der Mathematik hat der Monat 30 Tage.
>30 Silberlinge schenkte Judas.
>Es gab den Dreißigjährigen Krieg.

Noch mehr über die Zahl 30 gibt es auf den Seiten
http://zahlwort.blogger.de/stories/1069564
http://de.wikipedia.org/wiki/Drei%C3%9Fig
http://primes.utm.edu/curios/page.php/30.html
http://en.wikipedia.org/wiki/30_(number)
Das Internet sagt mir: Auch Zahlenmystiker kennen viele Geheimnisse um 30.

Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
https://www.mathematische-basteleien.de/

top