|
What is a Tetraflexagon?
... ... ... |
A tetraflexagon is a 2x2 square, which you can fold from
a strip of paper.
The point is: If you open the flexagon like a book on
the reverse side, then a new face appears, which was hidden before. |
In the simplest case the
tetraflexagon has three faces. It is called the tri-tetraflexagon, 3-4-flexagon.
Furthermore there are the tetra-, penta-, hexa-tetraflexagon
and so on with 4, 5, 6, ....faces.
Two Tri-tetraflexagons
top
How to make it
1
... ... ... |
Draw the figure of seven squares on checked paper and
cut it out.
Choose a=2cm e.g. as length of the square.
On this page the front side is green, the reverse side
is blue. |
2
...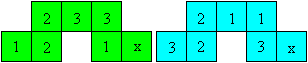 ... ... |
Write the numbers 1, 2, and 3 on the squares.
Two squares get the letter x. They will be glued on each
other later. |
3
|
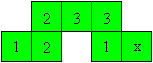
Fold the strip on the red line, so that the squares with
3 lie on each other. |
4
...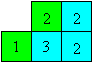 ... ... |
Push the square with 3 under the green square 2, so that
two 3s lie on each other. |
5
...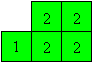 ... ... |
Glue the x-squares on each other on the reverse side.
 |
6
... ... ... |
The tri-tetraflexagon is finished. The front face has
the number 2, the reverse face 1. The number 3 is hidden.
 |
How to find the
third face
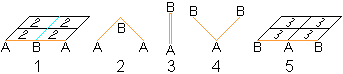 1 Turn the flexagon that face 2 is on top.
1 Turn the flexagon that face 2 is on top.
2 Fold the flexagon downwards. There is a mountain behind
B.
3 Lay the edges behind A and A on each other.
4 Open the flexagon like a book.
5 Spread out the flexagon on the plane. Face 3 is on
top.
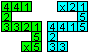
| You can describe this opening process by a diagram: |
 |
The two faces 12 stand at the beginning. The face 2 can be
opened, because 2 also stands on the right side of the line. The other
number on the right (3) is the face, which you can see after opening.
It is possible to go backwards.
You can open 2 and then face 1 appears.
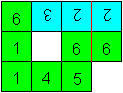
Descriptions
The flexagon has four squares,
but it is formed by six square sheets of paper. The sheet with x doesn't
count.
Two sheets lie on each other or
two sheets are single.
The single sheets lie in direction
of the diagonal \ , two layers in direction of the main diagonal /. It
doesn't depend on the numbers.
...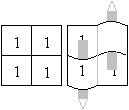 ... ... |
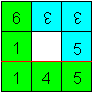
Faces 1 and 3 have two loops. A pencil shows them.
These are the faces, which you can't open and which become
"dead ends".
 |
... .. .. |
The face 2 has two points, which lie in direction of
\ .
These are squares, which are free on two sides.
This is the face you can open.

 |
Later on you will see that the
"higher" flexagons have a similar structure.
Mirror
image
...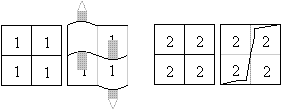 ... ... |
The flexagon is the same, if you
rotate by 180° around the centre of the flexagon.
If you reflect the tri-tetraflexagon
on the vertical centre line, you get a new flexagon. |
You can easily make it.
... ... ... |
If you reflect the template from above, you get a template
for this flexagon. |
The mirror image has the
same structure and gives no new aspects. Therefore you don't distinguish
between both forms.
Three Tetra-tetraflexagons
top
How to make the linear tetra-tetraflexagon
1
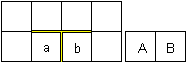
|
Draw the rectangles 4x2 and 2x1 and cut them out.
Cut along the yellow lines in the bigger rectangle.
Glue the square B on b. Then the square A lies over square
a.
 |
2
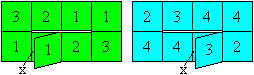
|
Write the numbers on the squares and x as shown on the
left. |
3
...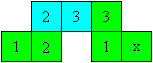 ... ...
|
Fold the strip so that the squares with the 4s lie on
each other.
The figure of the tri-tetraflexagon has developed. Lay
3 on 3 again and glue x on x.
 |
How
to open it
... ... ... |
Open the flexagon in the same way
as the tri-tetraflexagon.
This is shown in the diagram on
the left.
 |
How
to make the tetra-tetraflexagon with two dead ends
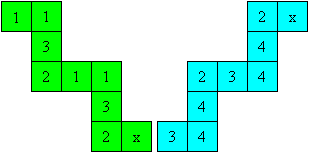
|
Make the template as shown on the left.
Lay the squares 4 on 4 twice.
Lay 3 on 3 twice, too.
Push the square x under the square.
Then x lies on x and another 1 on top.
Glue the x-squares on each other. |
... ... ... |
The special feature of this flexagon is that you only
get square 4, if you open the square 2 horizontally, starting at
32. This is described by writing 42 under 32 in the diagram.
 |
How
to make the cyclic tetra-tetraflexagon
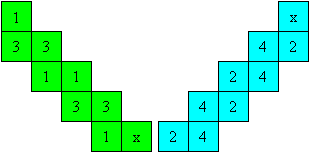
|
Prepare the template as shown on the left.
Lay the squares 4 on 4 twice.
Lay 3 on 3 twice, too.
Push the square x under the square.
Then x lies on x and another 2 on the top.
Glue the x-squares on each other. |
...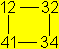 ... ...
|
It is special that this flexagon can be opened along
a circle.
 |
Cyclic Hexa-tetraflexagon
top
How to make it
1
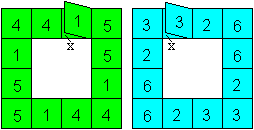
|
Make the template as shown on the left.
Lay the squares 6 on 6 twice.
Lay 5 on 5 twice, too. |
2
... |
Lay 4 on 4 twice and 3 auf 3 once.
 |
3
...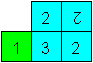 ... ... |
Push square 3 under the green square so that two 3s lie
on each other on the reverse side.
Fold 1 backwards and glue x on x. The flexagon is finished.
 |
Description
...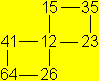 ... ... |
If you open the flexagon systematically you get the diagram
on the left.
It has the pattern of two squares with one corner in
common.
You go along two circles with the join 12.
 |
...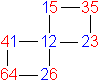 ... ... |
The faces 1 and 2 appear three times and form a cross.
The faces 3, 4, 5, and 6 appear twice and make the free
sides of the double square.
 |
...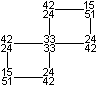 ... ... |
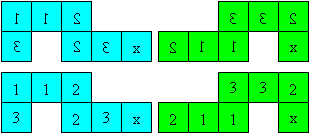
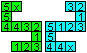
The flexagon consists of 12 sheets, which spread over
four squares. These squares can have 1, 2, 3 or 4 layers. Two squares side
by side have 1-5, 2-4 or 3-3 layers.
If you count all layers for every position of the flexagon,
you get the diagram on the left.
 |
You also can make the cyclic tetra-tetraflexagon without
gluing. You find descriptions on Arvind Gupta's web site (URL below).
More Tetraflexagons
top
Make the following papers by laying
squares on each other with the same numbers.
Start with the largest number and
go downwards.
| Penta-tetraflexagon with two dead
ends
|
Penta-tetraflexagon with one dead
end
|
Hexatetraflexagon
with two dead ends
| Septa-tetraflexagon with two dead
ends
|
Octa-tetraflexagon with two dead
ends
|
You find more tetraflexagons, if you glue two pairs of squares
with the same numbers on each other.
Tetraflexagon
with the Tube Flex top
How to make it
1

|
Make a template shown on the left.
Cut out also the squares inside. |
2
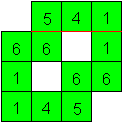
|
Fold on the red line. There is a valley.
 |
3
4
5
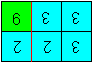
|
Fold on the red line.
Put the green square 6 on the left under the 3 next to
it.
 |
6

|
The tetraflexagon is finished.
 |
How
to open it
...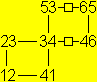 ... ...
|
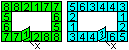
You find the faces 1 to 5 by the usual process of opening.
The paths between 53 and 65 and between 34 and 46 require
a new technique.
David Mitchell calls it "tube flex" (3). |
Tube Flex
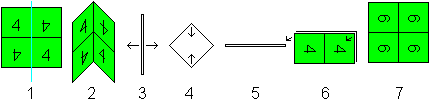
1 Look at face 4. Face 3 is on the reverse side.
2 Fold on the blue line. There is a mountain.
3 Open the flexagon to a tube.
4 Lay the lower and the upper corners on each other. |
5 Spread out the paper.
6 Turn over the flexagon vertically.
7 Open the flexagon. Face 6 is on the top.
. |
You find templates of these
kinds of flexagons in David Mitchell's book (3) or on Harold V. McIntosh's
web site (URL below).
There are more pages about
flexagons on my homepage: Flexagon, Flexatube,
and Hexahexaflexagon (German only).
Kaleidocycles can be
seen as three-dimensional flexagons.
Tetraflexagon
on the Internet top
German
Claus Michael Ringel
Flexagone
English
Eric W. Weisstein
Tetraflexagon
Harold V. McIntosh
Tetragonal
Flexagons
Wikipedia
Flexagon
Videos
YouTube
Flexagon
References
top
(1) Martin Gardner: The Second
Scientific American Book of Mathematical Puzzles & Diversions, New
York 1961
(2) Martin Gardner: Mathematische Denkspiele, München
1987 (ISBN 3 88034 323 3)
(3) David Mitchell: The Magic of Flexagons, Norfolk England
1998 (ISBN 1 899618287)
(4) Jill Russell: A Family of Tetraflexagons (http://www.sherston.freeserve.co.uk/HTML/Mathematics/JillsFlexagons.htm)
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
http://www.mathematische-basteleien.de/
©
2006 Jürgen Köller
top |

 ...
... ...
...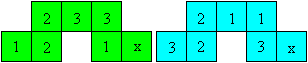 ...
...
 ...
... ...
... ...
... ...
... ..
.. ...
... ...
...

 ...
...



 ...
...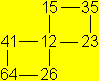 ...
... ...
...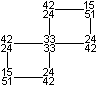 ...
...
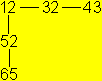
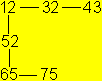
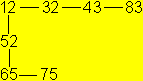




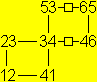 ...
...