Sangaku 
Inhalt dieser Seite
Was ist Sangaku?
Kreise im Kreis
Kreise im Dreieck
Kreise im Quadrat mit einem gotischen Bogen		 Drei Kreise
Weitere Sangaku-Figuren an anderen Stellen
Sangaku - eine kommentierte Liste von Hyperlinks
.
Zur Hauptseite    "Mathematische Basteleien"

Was ist Sangaku?
...... Mit Sangaku (San Gaku) bezeichnet man geometrische Probleme (meist Berührprobleme) der euklidischen Geometrie. Sie entstanden in Japan während der Edo-Periode (1603–1867) und sind uns als farbige Zeichnungen auf hölzernen Tafeln auf Shinto-Schreinen oder in buddhistischen Tempeln überliefert.
Wir fassen sie als Aufgaben auf. Ursprünglich waren sie wohl eher Schaustücke mit Erläuterungen und Anregungen, sich über sie Gedanken zu machen.

Bei den Recherchen für meine Webseite Kreise in einer Figur stieß ich zuletzt wieder auf Figuren der "japanischen Tempelgeometrie". 
Entsprechend ist die Wahl der Figuren auf dieser Webseite ausgefallen.

Kreise im Kreis      top
Arithmetisches Mittel
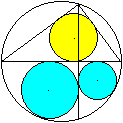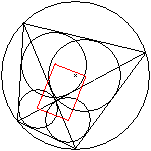
...... Gegeben seien ein Kreis und ein einbeschriebenes, rechtwinkliges Dreieck mit seinem Inkreis. Der freie Halbkreis wird durch die Verlängerung der Dreieckshöhe in zwei Teilfiguren aufgeteilt, in der auch Kreise liegen. In welcher Beziehung stehen die Radien der drei Kreise?

Quelle: (1) Problem 18 mit Lösung    (URL unten)
Es gilt: Der Radius des Inkreises ist das arithmetische Mittel der Radien der Kreise in den Teilfiguren.

Beweis
Größen
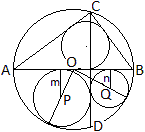Das rechtwinklige Dreieck ABC habe den Umkreis mit dem Mittelpunkt O und den Radius R. 
Der Inkreis habe den Radius r. Die Höhe des Dreiecks sei (1/2)CD.
Die beiden Kreise unten sollen die Mittelpunkte P und Q und die Radien m und n haben.
Der Abstand des Punktes O von CD sei d.
Bestimmung der Radien m und n
Für die eingezeichneten rechtwinkligen Dreiecke gilt der Satz des Pythagoras.
Für das linke Dreieck gilt (R-m)² = m²+(m-d)².
Dann  ist R²-2Rm+m² = m²+m²-2dm+d² oder m²-2dm+2Rm+d²-R² = 0 oder m²+2(R-d)m-(R²-d²) = 0.
Die quadratische Gleichung führt zur positiven Lösung 
m = -(R-d)+sqrt[(R-d)²+(R²-d²)] oder m = -(R-d)+sqrt[2R(R-d)].

Für das rechte Dreieck gilt (R-n)² = n²+(n+d)².
Dann  ist R²-2Rn+n² = n²+n²+2dn+d² oder n²+2dn+2Rn+d²-R² = 0 oder n²+2(R+d)n-(R²-d²) = 0.
Die quadratische Gleichung führt zur positiven Lösung 
n = -(R+d)+sqrt[(R+d)²+(R²-d²)] oder n = -(R+d)+sqrt[2R(R+d)].

Berücksichtigung der Katheten
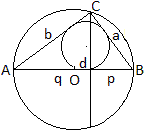Man führt im rechtwinkligen Dreieck die Achsenabschnitte p und q mit p+q=c ein.

Dann gilt nach dem Kathetensatz pc=a². Mit p=R-d ist (R-d)c=a² oder a = sqrt[2R(R-d)].
Nach dem Kathetensatz gilt weiter qc=b². Mit q=R+d ist (R+d)c=b² oder b = sqrt[2R(R+d)]. 
Das bedeutet für die Radien m und n:
m = -(R-d)+sqrt[2R(R-d)] = -(R-d)+a = a+d-R
n = -(R+d)+sqrt[2R(R+d)] = -(R+d)+b = b-d-R
Mittelwert
Dann ist der Mittelwert (1/2)(m+n) = (1/2)(a+b-2R) = (1/2)(a+b-c) 
Im rechtwinkligen Dreieck gilt für den Radius des Inkreises die Formel r=(1/2)(a+b-c). 
Und das ist gerade der Mittelwert der Kreise mit den Radien m und n, was zu beweisen war.
Zusatz
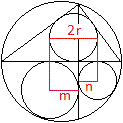...... Zeichnet man durch die Mittelpunkte der unten liegenden Kreise die Vertikalen, so berühren sie den oberen Kreis. 
Die Verbindungslinie dieser Berührpunkte ist der Durchmesser des oben liegenden Kreises.
Da kann man unmittelbar ablesen: 2r=m+n oder r=(1/2)(m+n).
Diese besondere Lage der Kreise geht aus den bisherigen Überlegungen nicht hervor und müsste bewiesen werden.
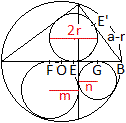Es muss gezeigt werden, dass Punkt E die Strecke FG halbiert oder dass EG = r ist. 

Dazu setzt man die Gleichungen n = b-d-R und r = (1/2)(a+b-2R) bzw. 2r = a+b-2R von oben ein.
Es gilt EG = EB-GB = (a-r)-(R-d-n) = (a-r)-(R-d-b+d+R)=(a-r)-(2R-b) = (a-r)-(a-2r) = r, wzbw. 
Ein Inkreis in der Zweikreisfigur
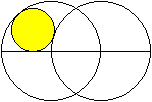...... Gegeben ist die Zweikreisfigur aus gleichen Kreisen, bei der der Mittelpunkt des einen Kreises auf der Kreislinie des anderen Kreises liegt. Gesucht ist der Radius des Kreises, der den gemeinsamen Durchmesser, einen Kreis innen und den anderen außen berührt.

Quelle: Alexander Bogomolny,  Problem 33 mit einer Lösung   (URL unten)
Lösung
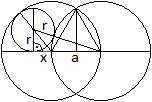...... Die Radien der Kreises sei a, der Radius des gesuchten Kreises r. Eine Hilfsstrecke x ist rot markiert.
Dann gilt im großen rechtwinkligen Dreieck nach dem Satz des Pythagoras (a+r)² = r²+(a+x)², im kleinen (a-r)² = r²+x². Das sind zwei Gleichungen in den Variablen r und x. 
Man eliminiert die Hilfsvariable x und erhält nach etlichen Rechenschritten r=(1/4)sqrt(3)a.
Das bedeutet, dass der Durchmesser des Kreises gleich der Höhe des gleichseitigen Dreiecks der Seitenlänge a ist.
Drei Kreise oberhalb eines Kreisbogens im Kreis
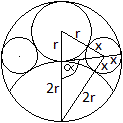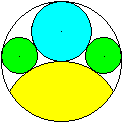
...... ...... Gegeben ist in der Figur der Radius r des blauen Kreises. Dann sind die Radien des umfassenden Kreises und des Kreisbogens 2r. Gesucht ist der Radius x des grünen Kreises.

Nach dem Kosinussatz gilt für die beiden Teildreiecke
(r+x)² = r²+(2r-x)²+2r(2r-x)cos(alpha) und (2r+x)² = 4r²+(2r-x)²-4r(2r-x)cos(alpha).
Das sind zwei Gleichungen in den Variablen alpha und x. 
Es ist günstig, in beiden Gleichungen die Terme mit cos(alpha) zu isolieren.
Es ist 2r(2r-x)cos(alpha) = (r+x)²-r²-(2r-x)² oder 4r(2r-x)cos(alpha) = 2(r+x)²-2r²-2(2r-x)² 
und 4r(2r-x)cos(alpha) = 4r²+(2r-x)²-(2r+x)²
Die rechten Terme werden gleichgesetzt: 2(r+x)²-2r²-2(2r-x)² = 4r²+(2r-x)²-(2r+x)².
Es ergibt sich nach einigen Rechenschritten die Lösung x=(3/5)r.
Quelle: http://commons.wikimedia.org/wiki/File:Sangaku_of_Konnoh_Hachimangu_1859.jpg
Zwei Kreise und ein gleichschenkliges Dreieck in einem Kreis
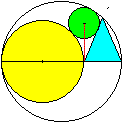...... Gegeben sei ein Kreis und ein zweiter, kleinerer Kreis, der den großen innen berührt. Zeichnet man durch den Berührpunkt einen horizontal liegenden Durchmesser, so wird dieser in zwei Teilstrecken aufgeteilt. Man errichtet über die freie Teilstrecke ein gleichschenkliges Dreieck. Legt man einen (grünen) Kreis in die Figur, der den großen innen, den gelben Kreis außen und den Schenkel des Dreiecks außen berührt, so liegt sein Mittelpunkt vertikal über dem Teilpunkt des Durchmessers.
Lösungen bei Ingmar Rubin (URL unten), Alexander Bogomolny, Problem 59  (URL unten), Ken Duesenberg (URL unten)

Kreise im Dreieck     top
Ein Dreieck und 17 Kreise
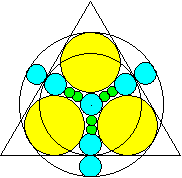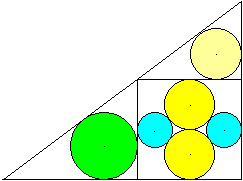
...... Gegeben sei der Radius c eines grünen Kreises.
Gesucht sind der Radius R des großen Kreises, des Inkreises des Dreiecks r, eines gelben Kreises a und eines blauen Kreises b.

Man liest unmittelbar ab: a+b = 2b+4c, r = 3b+4c, R = 5b+4c, R = b+2a
Daraus ergibt sich a=6c, b=2c, r=10c und R=14c.

Quelle: Alexander Bogomolny, Problem11 (URL unten)

Kreise im rechtwinkligen Dreieck 
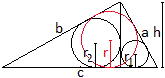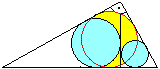
...... ...... Gegeben sei ein rechtwinkliges Dreieck mit dem Inkreis. Die Höhe h teilt es in zwei kongruente Teildreiecke auf, in denen auch die Inkreise eingezeichnet sind. 
Wie lässt sich die Höhe des Dreiecks aus den Radien berechnen?
Lösung: h=r+r1+r2
Quelle:  Alexander Bogomolny, Problem 61 mit Lösung   (URL unten)
Herleitung
Auf meiner Webseite Rechtwinkliges Dreieck findet man die Formeln r=ab/(a+b+c), r1=(a/c)r, r2=(b/c)r und h=(ab)/c.
Dann gilt r+r1+r2 =  r+(a/c)r+(b/c)r = (1+a/c+b/c)*r = [(a+b+c)/c]*[ab/(a+b+c)]=(ab)/c = h, wzbw..
Zwei gleiche Kreise im Dreieck
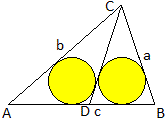...... Gegeben sei das Dreieck ABC durch die Seitenlängen a, b und c. In das Dreieck wird eine Strecke so gelegt, dass die Inkreise der Teildreiecke gleich groß sind. Wie lang ist diese Strecke?
Lösung: DC=sqrt[s(s-c)] mit s=(1/2)(a+b+c)

Quelle: Alexander Bogomolny, Problem 67 mit Lösung  (URL unten).
Herleitung der Formel
Flächenbetrachtung
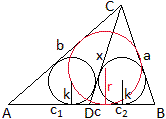Es sei s=(1/2)(a+b+c), s1=c1+x+b und s2=c2+a+x.
Dann gilt (#) s1+s2= s+x, denn es ist s1+s2 = (1/2)(c1+x+b)+(1/2)(c2+a+x) = (1/2)(a+b+c)+x = s+x.

Weiter sei r der Radius des Inkreises des Dreiecks ABC, k seien die Radien der Inkreise der Teildreiecke. 
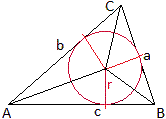Für den Flächeninhalt des Dreiecks ist A = (1/2)cr+(1/2)ar+(1/2)br=(1/2(a+b+c)r=sr.
Andererseits ist der Flächeninhalt des Dreiecks gleich der Summe der Flächeninhalte der Teildreiecke:
A1+A2 = [(1/2)c1k+(1/2)xk+(1/2)bk]+[(1/2)c2k+(1/2)ak+(1/2)xk] =(1/2)k(c1+x+b)+(1/2)k(c2+x+a) = (s1+s2)k.
Dann gilt wegen (#) s1+s2= s+x die Gleichung  (*) sr = (s+x)k.
Proportionen
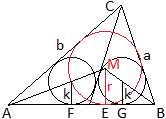Verbindet man den Mittelpunkt des Inkreises mit den Eckpunkten A und B, so entstehen die rechtwinkligen Dreiecke AEM und EBM. 
Nach dem 2. Strahlensatz gilt AF:AE = k:r und BG:BE = k:r.

Es gilt AE = s-c, AF = s1-x, BE = s-a und BG = s2-x, wie die folgenden Überlegungen zeigen. 
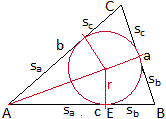Es wird an Hand der nebenstehenden Zeichnung gezeigt, dass AE = s-a gilt.
Für ein beliebiges Dreieck mit Inkreis gilt für die eingezeichneten Tangentenabschnitte 
sa=s-a, sb=s-b und sa=s-c, wobei s=(1/2)(a+b+c) ist.
Es gilt z.B. s-a = (1/2)(a+b+c)-a = (1/2)(2sa+2sb+2sc)-a = sa+sb+sc-a = sa+a-a= sa
Entsprechend ergeben sich die anderen drei Gleichungen AF=s1-x, BE=s-b und BG=s2-x.
Damit führen die Gleichungen AF:AE = k:r und BG:BE = k:r zu den Proportionen (s1-x):(s-a) = k:r und (s2-x):(s-b) = k:r.
Dann ist (s1-x)r = (s-a)k oder s1-x =(k/r)(s-b)  und (s2-x)r = (s-a)k oder s2-x = (k/r)(s-a).
Man addiert die rechten und linken Terme,
s1-x + s2-x = (k/r)(s-b)+(k/r)(s-a) oder s1+s2-2x = (k/r)(s-b+s-a) oder s1+s2-2x = (k/r)c.
Mit (#) s1+s2 = s+x ergibt sich s-x = (k/r)c oder (**) sr-rx = kc. 
Zusammenführung
Man hat somit zwei Gleichungen zur Verfügung, nämlich (*) sr = (s+x)k und (**) sr-rx = kc, um die Suchvariablen x (und k) zu bestimmen. 
Man multipliziert z.B. beide Seiten der ersten Gleichung mit c und ersetzt kc durch den Term sr-rx und erhält src = (s+x)(sr-xr). 
Dann ist sc = (s+x)(s-x) oder sc = s²-x². Daraus ergibt sich x² = s²-sc oder x = sqrt[s(s-c)], wzbw.

Kreise im Quadrat mit einem gotischen Bogen     top
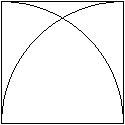...... Zwei Viertelkreise in einem Quadrat bilden den "gotischen Bogen".

Sein Kennzeichen ist eine Spitze oben.

......
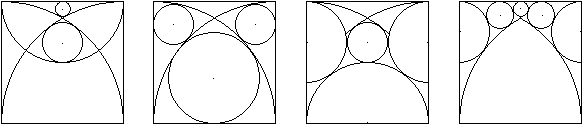
 Man kann in das Quadrat unter Einbeziehung der Viertelbögen eine Reihe von Kreisen einpassen, deren Radien von Interesse sind.
Quelle: Alexander Bogomolny: 47 Sangaku and The Egyptian Triangle (URL unten)
Größter Kreis
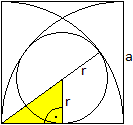...... Die Seitenlänge des Quadrates sei a.

Nach dem Satz des Pythagoras gilt (a-r)² = r²+(a/2)².

Nach einigen Rechenschritten ergibt sich r=(3/8)a.

Kleinster Kreis
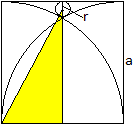...... Nach dem Satz des Pythagoras gilt (a+r)² = (a-r)²+(a/2)².

Nach einigen Rechenschritten ergibt sich r=(1/16)a.

Mittlerer Kreis
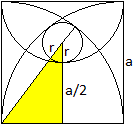...... Der Halbkreis hat den Radius (1/2)a.
Nach dem Satz des Pythagoras gilt (a-r)² = (a/2)²+(a/2+r)².

Nach einigen Rechenschritten ergibt sich r=(1/6)a.

Kreis in der Ecke
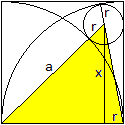...... Es treten zwei rechtwinklige Dreiecke auf.
Nach dem Satz des Pythagoras gilt im rechten Dreieck (a-r)² = x²+r².
Nach dem Satz des Pythagoras gilt im linken Dreieck (a+r)² = x²+(a-r)².
Nach einigen Rechenschritten ergibt sich r=(1/6)a.
Halbkreis links oben
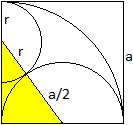...... Nach dem Satz des Pythagoras gilt (a/2+r)² = (a-r)²+(a/2)².

Nach einigen Rechenschritten ergibt sich r=(1/3)a.

Halbkreis rechts oben
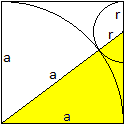...... Nach dem Satz des Pythagoras gilt (a+r)² = (a-r)²+a².

Nach einigen Rechenschritten ergibt sich r=(1/4)a.

Kreis rechts oben
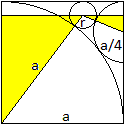...... Es treten zwei rechtwinklige Dreiecke auf.

Nach dem Satz des Pythagoras gilt im rechten Dreieck (a/4+r)² = x²+(a/4-r)².
Nach dem Satz des Pythagoras gilt im linken Dreieck (a+r)² = (a-x)²+(a-r)².
Nach etlichen Rechenschritten ergibt sich r=(1/9)a.

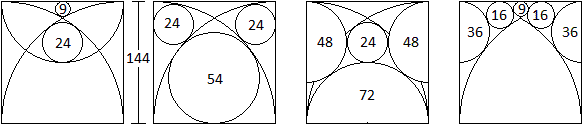
Zusammenfassung
Wählt man als Länge des Quadrates 144 LE, so werden alle Radien ganzzahlig. Sie stehen in den jeweiligen Kreisen. 
 
......
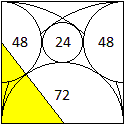...... Das Besondere ist, dass in den Figuren auch pythagoräische Dreiecke mit den Seitenlängen 3, 4 und 5 auftauchen.

Darauf gehe ich auf meiner Webseite 3-4-5-Dreieck ein.

Drei Kreise (Three tangent circles)  top
Kreis unter zwei Kreisen
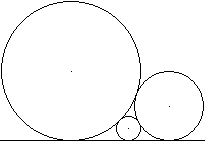
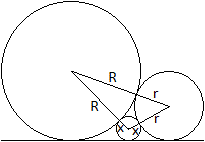
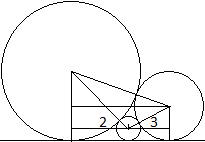
...... Drei Kreise berühren eine Gerade und sich untereinander von außen. 

In welcher Beziehung stehen die Radien der Kreise?

Quelle: Alexander Bogomolny, Problem 63, siehe auch Kevin Mirus, Problem 1.1.0
(URL unten)

Lösung
Die Radien sollen R, r und x sein. Verbindet man die Mittelpunkte der Kreise, ergibt sich ein Dreieck mit den Seiten R+r, r+x und R+x. 
Man ergänzt das Dreieck um drei rechtwinklige Dreiecke, dessen horizontal liegende Katheten s1, s2 und s3 sein sollen. 
Nach dem Satz des Pythagoras gelten die Gleichungen (R+r)² = (R-r)²+s1², (R+x)² = (R-x)²+s2² und (r+x)² = (r-x)²+s3².
Aus den Gleichungen folgt 4Rr =s1², 4Rx = s2² und 4rx = s3².
Aus s1 = s2 + s3 folgt sqrt(4Rr) = sqrt(4Rx)+sqrt(4rx) oder 1/sqrt(x) = 1/sqrt(R)+1/sqrt(r).
Es folgen vier Varianten der Aufgabe.
Gleiche Kreise rechts und links
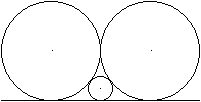...... Die Kreise rechts und links seien gleich. Dann ist der Radius des Kreises in der Mitte viermal so klein wie der eines großen Kreises.

Es gilt 1/sqrt(x) = 2/sqrt(R) oder 1/x=4/R oder x = (1/4)R.
Quadrat unter zwei gleichen Kreisen
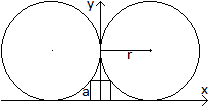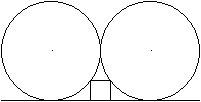
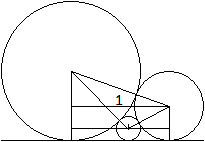
...... ...... Gegeben sei der Radius r eines Kreises, gesucht ist die Seitenlänge a des Quadrates. Zur Berechnung führt man ein Koordinatensystem ein. Der rechte Kreis hat die Darstellung (x-r)²+(y-r)²=r². Der Punkt P[(1/2)a|a] muss auf dem Kreis liegen. Das führt zur Bestimmungsgleichung [(1/2)a-r]²+(a-r)²=r². 
Sie wird gelöst von a1=r und a2=(2/5)r. 
Ergebnis: Das Quadrat hat eine Seitenlänge von a=(2/5)r. - Entdeckt bei Antonio Gutierrez , Problem 336 (URL unten)
Weitere Kreise in der Mitte
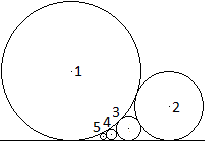...... Fügt man wie links noch weitere Kreise hinzu, 
so gilt 1/sqrt(rn) = (n-2)/sqrt(r1)+1/sqrt(r2)    (n=3,4,5,...).

Quelle: Alexander Bogomolny, Problem 15 mit Lösung    (URL unten)
Kreise mit ganzzahligen Radien
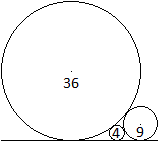...... In der Gleichung 1/sqrt(x) = 1/sqrt(R)+1/sqrt(r) können für x=4, R=36 und r=9 die Wurzeln gezogen werden.
Dann wird 1/sqrt(x) = 1/sqrt(R)+1/sqrt(r) zu 1/2=1/6+1/3.
Setzt man auf das Problem ein Computer-Programm an, so findet man viele Tripel, die die Gleichung erfüllen. Die ersten Tripel, die der Computer für (x,R,r) fand, sind (1,4,4), (4,16,16), (4,36,9), (9,144,16), (9,36,36), (16,64,64), (16,144,36), ...

Quelle: http://en.wikipedia.org/wiki/Sangaku    (URL unten)
Drei Kreise zwischen Parallelen 1
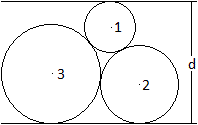...... Gegeben sind drei sich von außen berührende Kreise mit den Radien r1, r2 und r3, die wie links zwischen zwei Parallelen liegen. Gesucht ist der Abstand der Parallelen.
Lösung:

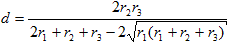Quelle: Kevin Mirus, Problem 1.2.3 mit Lösung   (URL unten)
Drei Kreise zwischen Parallelen 2
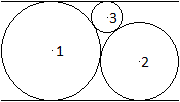...... Gegeben sind drei sich von außen berührende Kreise mit den Radien r1, r2 und r3, die wie links zwischen zwei Parallelen liegen. Wie groß ist der Radius des großen Kreises, wenn die beiden anderen Radien gegeben sind?
Lösung: r1² = 4r2r3 oder r1= 2sqrt(r2r3)

Quelle: Kevin Mirus,  Problem 1.2.4  mit Lösung    (URL unten)

Weitere Sangaku-Figuren an anderen Stellen    top

Rechteck im Viereck

Sechs Kreise im Dreieck

Fünf gleiche Kreise im Quadrat 2

Sangaku - eine kommentierte Liste von Hyperlinks     top
 
Sangaku  (http://de.wikipedia.org/wiki/Sangaku) Sangaku  (http://en.wikipedia.org/wiki/Sangaku)

Da verschafft man sich einen ersten Überblick.

Tafeln bei Wikipedia
Tafel 1
Tafel 2
Tafel 3
Tafel 4
Ingmar Rubin
Sangaku-Probleme
Aufgaben aus der japanischen Tempelgeometrie mit Lösung
Sangaku - Probleme
Aufgaben aus der japanischen Tempelgeometrie
ein Beitrag von Ingmar Rubin, Berlin
Alexander Bogomolny  (cut-the-knot)
1 Sangaku: Reflections on the Phenomenon (http://www.cut-the-knot.org/pythagoras/Sangaku.shtml) 
Eine umfassende Darstellung von Sangaku mit einer Sammlung von 67 Problemen (November 2013)
Im Einführungstext wird aus dem Buch [H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989] zitiert. Offenbar ist das das erste Standardbuch der Sangaku-Bewegung.
Ich habe die folgenden Aufgaben ausgewählt. 
11 Sangaku by a teen, 15 Ancient Morsel,  18 Arithmetic Mean Sangaku, 33 Likely Sangaku, 
47 Sangaku and The Egyptian Triangle, 59 Tangent Circles And Regular Triangle, 
61 Three Incircles In a Right Triangle, 63 Three Tangent Circles Sangaku, 67 Two Sangaku with Equal Incircles
Hidetoshi Fukagawa und Tony Rothman
Sangaku: Japanische Geometrie (https://www.spektrum.de/magazin/sangaku-japanische-geometrie/824657)
Aus Spektrum 01.07.1998  (deutsch)
Hiroshi Okumura
JAPANESE MATHEMATICS   (https://www.researchgate.net/publication/266983506_Japanese_mathematics)
Der Japaner Hiroshi Okumura beschreibt Wasan, die japanischen Geometrie in der Edo-Periode. Sangaku ist ein Teilbereich.
Hiroshi Kotera
Japanese Temple Geometry Problem - Sangaku   (http://www.wasan.jp/english/)
Das Besondere ist eine Karte Japans, durch die man erfahren kann, wo Tafeln gefunden wurden und wie sie aussehen.
Géry Huvent 
Sangaku    (http://gery.huvent.pagesperso-orange.fr/html/sangaku.htm)
Eine französische Site mit neuen Figuren
Antonio Gutierrez (GeoGeometrie) 
Sangaku Problems - Table of Content
(http://gogeometry.com/math_geometry_online_courses/sangaku_japanese_geometry_table_index.html)
Unter den über 600 (!) Problemen der euklidischen Geometrie findet man auch acht der Tempelgeometrie.
Hier ist noch der Hinweis, dass man oft hilfreiche Kommentare oder sogar Lösungen auf den Seiten über den Link Post a comment oder Solution/Comment findet.
Ich habe ein Problem aufgenommen:
Problem 336 Two equal circles, a Common Tangent and a Square 
J. Marshall Unger
A Collection of 30 Sangaku Problems (pdf.file)
Martin Geppel
Sangaku - Japanische Tempelgeometrie
Wie heilige Holztafeln den Mathematikunterricht bereichern können
Homepage zur Diplomarbeit von Martin Geppel

Mathias Dietrich (Kawaraban - Alles über Japan, von der Kultur bis hin zur Sprache!)
Sangaku: Mathetest als Opfergabe (https://kawaraban.de/sangaku-japan-tempelgeometrie/)
Ken Duesenberg
A Sangaku Problem
 Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
http://www.mathematische-basteleien.de/

©  2013 Jürgen Köller

top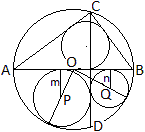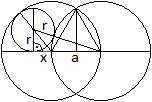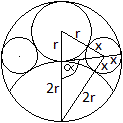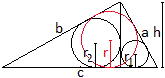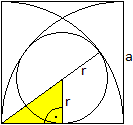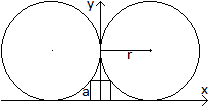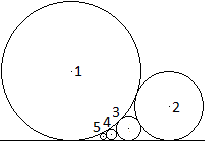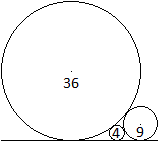