|
Was ist ein Rechteck?
... ... ... |
...Ein
Rechteck ist - dem Wort folgend - ein Viereck mit rechten Winkeln.... |
... ... ... |
Auch das Quadrat ist ein Rechteck.
Es hat zusätzlich gleich lange Seiten und ist so
ein Sonderfall des Rechtecks. |
Formeln top
Grundformeln
...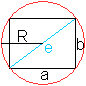 ... ... |
Größen des Rechtecks sind
die Seiten a und b, die Diagonale e,
der Radius des Umkreises R, der Umfang U und der Flächeninhalt
A. |
Im Allgemeinen ist ein
Rechteck durch die Seiten a und b gegeben.
Daraus lassen sich die übrigen
Größen berechnen.
Abstand von
der Diagonalen
...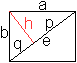 . . |
Gegeben ist ein Rechteck mit den Seiten a und b.
Gesucht ist der Abstand h eines Eckpunktes von der Diagonalen
e. |
Lösung
Man führt die Hilfsgrößen p und q ein.
Nach dem Kathetensatz gilt a²=pe und b²=qe oder p=a²/e und
q=b²/e.
Nach dem Höhensatz gilt h²=pq=(a²/e)(b²/e)=(a²b²/e²)=(a²b²)/(a²+b²)
oder h=(ab)/[sqrt(a²+b²)].
Ergebnis: Der Eckpunkt hat einen Abstand von h=(ab)/[sqrt(a²+b²)].
Einige besondere
Rechtecke top
Goldenes Rechteck
...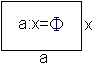 ... ... |
Ein Rechteck heißt Goldenes Rechteck, wenn das
Seitenverhältnis Phi=(1/2)[sqrt(5)+1] ist. |
...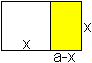 ... ... |
Das ist auffällig:
Zeichnet man in das Rechteck ein Quadrat, so ist das
Rest-Rechteck wieder ein Goldenes Rechteck. |
Mehr findet man auf meiner Seite Goldener
Schnitt.
Papierformat
A4
...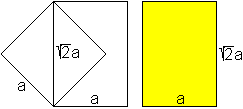 ... ... |
Das Rechteck aus der Seite und der Diagonalen eines Quadrat
hat die Form eines Blattes der A-Reihe. |
... ... ... |
Das ist auffällig:
Man kann das Rechteck so halbieren, dass das Seitenverhältnis
erhalten bleibt. |
Mehr findet man auf meiner Seite Papierformat
A4.
Es folgt eine Zusammenstellung einiger
Rechtecke.
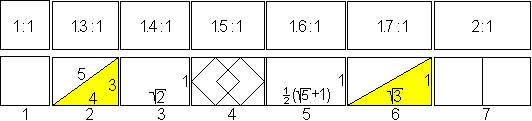 1) Quadrat, 2) 3-4-5-Dreieck und seine Spiegelung, 3) Papierformat
der A-Reihe, 4) Rechteck um zwei verkettete Quadrate, 5) Goldenes Rechteck,
6) 30-60-90-Dreieck und seine Spiegelung oder das gleichseitige Dreieck
- neu zusammengesetzt, 7) Doppelquadrat
1) Quadrat, 2) 3-4-5-Dreieck und seine Spiegelung, 3) Papierformat
der A-Reihe, 4) Rechteck um zwei verkettete Quadrate, 5) Goldenes Rechteck,
6) 30-60-90-Dreieck und seine Spiegelung oder das gleichseitige Dreieck
- neu zusammengesetzt, 7) Doppelquadrat
Quadratur des
Rechtecks top
Es geht darum, zu einem Rechteck ein flächengleiches
Quadrat zu bestimmen.
...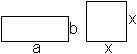 ... ... |
Die Rechenaufgabe ist problemlos. Aus ab=x² folgt
x=sqrt(ab). |
Die klassische Aufgabe bezieht sich
auf die Konstruktion des Quadrates.
... ... ... |
... ... ... |
 ... ... |
 ... ... |
Am bekanntesten sind vier Lösungen, die auf den
Kathetensatz, den Höhensatz, den Sekanten-Tangenten-Satz und den Sehnensatz
zurückgehen. |
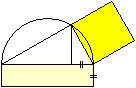
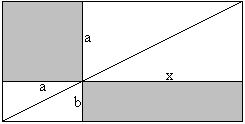
Die Konstruktion nach dem Sekanten-Tangenten-Satz
könnte so aussehen.
 1 Trage die kleinere Seite des Rechtecks auf der größeren
ab.
1 Trage die kleinere Seite des Rechtecks auf der größeren
ab.
2 Zeichne die Mittelsenkrechte und nehme auf ihr einen
Punkt an.
3 Zeichne einen Kreis.
4 Verbinde einen Eckpunkt des Rechtecks mit dem Kreismittelpunkt.
5 Zeichne den Halbkreis des Thales.
6 Zeichne die Tangente.
7 Errichte über dem Tangentenabschnitt ein Quadrat.
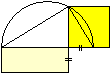
Die Konstruktion nach dem Sehnensatz könnte
so aussehen.
 1 Verlängere die größere Seite des Rechtecks
um die kleinere.
1 Verlängere die größere Seite des Rechtecks
um die kleinere.
2 Zeichne die Mittelsenkrechte und nehme auf ihr einen
Punkt an.
3 Zeichne den Kreis.
4 Verbinde einen Eckpunkt des Rechtecks mit dem Kreismittelpunkt.
5 Zeichne die senkrechte Gerade durch einen Eckpunkt
des Rechtecks.
6 Errichte über die halbe Sehne das Quadrat.
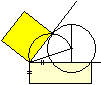
Die Konstruktionen zum Kathetensatz
und zum Höhensatz findet man bei Jürgen Ullwer (URL unten)
... ... ... |
Auch das "Ergänzungsparallelogramm" enthält
ein Quadrat und ein flächengleiches Rechteck. Die Figur ist aber nicht
geeignet, das Quadrat zu finden.
Man kann aber vom Quadrat zum flächengleichen Rechteck
gelangen. |
Vierecke und Rechtecke
top
Zwei Mittenvierecke
...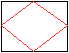 ... ... |
Verbindet man die Mittelpunkte der Seiten eines Rechtecks,
so entsteht eine Raute. |
... ... ... |
Verbindet man die Mittelpunkte der Seiten einer Raute,
so entsteht ein Rechteck. |
Rechteck im
Viereck
...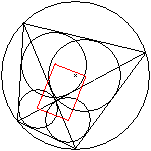 ... ... |
Zeichnet man in ein Sehnenviereck die Diagonalen und
in die Teildreicke die Inkreise ein, so bilden die Mittelpunkte dieser
Kreise ein Rechteck. |
Eine Darstellung und einen Beweis
findet man auf der Homepage von Antonio Gutierrez unter dem Namen Sangaku
Problem (URL unten).
Rechteck im Rechteck
top
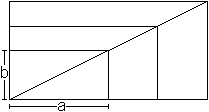
Gegeben sei ein Rechteck mit den
Seitenlängen a und b. In ihm soll ein Rechteck mit einer bekannter
Seitenlänge k wie in der Skizze dargestellt eingepasst werden. Gesucht
ist die zweite Seitenlänge d.
... ... ... |
Es entstehen in den Ecken ähnliche rechtwinklige
Dreiecke, deren Katheten x und y bzw. b-x und a-y sind.
Das wird ausgenutzt, um für die drei Suchvariablen
x, y und d drei Formeln aufzustellen.
Wegen der Ähnlichkeit der Dreiecke gilt (#) x:d
= (a-y):k und (##) y:d = (b-x):k.
Nach dem Satz des Pythagoras gilt (###) k² = (b-x)²+(a-y)². |
Die Berechnung der Variablen d ist umfänglich und führt
schließlich zu einer Gleichung vierten Grades:
(d²)² - (2k²+a²+b²)d² +
(4abk)d + [(k²)²-a²k²-b²k²] =0
Ich setze aus schreibtechnischen Gründen (d2)2
= d4.
Rechnung
Die Variablen x und y werden zunächst mit Hilfe
der Gleichungen (#) und (##) bestimmt.
x:d = (a-y):k und y:d = (b-x):k
<=> kx = d(a-y)und yk = d(b-x)
<=> kx = ad-dy und yk = bd-dx
<=> dy = ad-kx und ky = bd-dx
<=> dky = adk-k²x und dky = bd²-d²x
<=> adk-k²x = bd²-d²x
<=> -k²x+ d²x = bd²-adk
<=> x = (bd²-adk)/(d²-k²) |
x:d = (a-y):k und y:d = (b-x):k
<=> kx = d(a-y)und yk = d(b-x)
<=> kx = ad-dy und yk = bd-dx
<=> kx = ad-dy und dx = bd-ky
<=> dkx = ad²-d²y und dkx = bdk-k²y
<=> ad²-d²y = bdk-k²y
<=> d²y-k²y = ad²-bdk
<=> y = (ad²-bdk)/(d²-k²) |
Die Gleichung (###) k²
= (b-x)²+(a-y)² wird zu k² = b²-2bx+x²+a²-2ay+y²
umgeformt.
Man setzt zur Vereinfachung x²+y² = d²
und an Stelle von x und y die vorher bestimmten Terme.
k² = b²-2b(bd²-adk)/(d²-k²)+a²-2a(ad²-bdk)/(d²-k²)+d²
Beide Seiten der Gleichung werden mit dem Term d²-k²
multipliziert.
k²(d²-k²) = b²(d²-k²)-2b²d²+2abdk+a²(d²-k²)-2a²d²+2abdk+d²(d²-k²)
Es wird ausmultipliziert.
k²d²-(k²)² = b²d²-b²k²-2b²d²+2abdk+a²d²-a²k²-2a²d²+2abdk+(d²)²-k²d²
Es wird geordnet und zusammengefasst.
(d²)²-2k²d²+b²d²-2b²d²+a²d²-2a²d²+4abdk-b²k²-a²k²+(k²)²
= 0
(d²)²-2k²d²-b²d²-a²d²+4abdk-b²k²-a²k²+(k²)²
= 0
(d²)²-(-a²-b²-2k²)d²+4abdk+[(k²)²-a²k²-b²k²]
= 0
Es ergibt sich also eine Gleichung vierten Grades in d.
(d²)² - (2k²+a²+b²)d² +
(4abk)d + [(k²)²-a²k²-b²k²] =0.
Es ist wohl wenig sinnvoll und auch abschreckend zu versuchen,
die gesuchte Variable d durch einen Term anzugeben.
An einem Zahlenbeispiel kann man die Brauchbarkeit der
Gleichung überprüfen.
...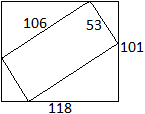 ... ... |
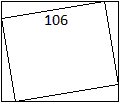
Ich fand im Internet auf der Webseite von David Broughton
(URL unten) eine Lösung dieses Rechteckproblems mit den ganzzahligen
Längenangaben wie in der Zeichnung.
Setzt man in die allgemeine Gleichung 4. Grades a=118,
b=101 und k=106 ein, so heißt die Gleichung
(d²)²-46.597*d²+5.053.232*d-144.820.804
= 0.
Mit Hilfe des Applets von Arndt Brünner (URL unten)
fand ich die Lösungen
d1= -260,9, d2=53 (!), d3
= 85,58 und d4 = 122,4. |
Die maßstabsgetreue Zeichnung hält die Lösung
d2=53 fest. Damit die Zeichnung gelingt, habe ich noch x=45
und y=28 berechnet.
... ... ... |
Es gibt noch eine zweite Lösung (!), nämlich
d3 = 85,58. Für sie sind x=84,54 und y=13,29.
Die Lösungen d1 und d4 sind
für das Problem unbrauchbar. |
Auf dieses Problem stieß
Axel Ridtahler, als er ein rechteckiges Brett in eine rechteckige Kiste
diagonal einpasste.
Dabei kam ihm die gute ;-) Idee, mich auf dieses Problem
hinzuweisen.
Quadrate
im Rechteck top
Fläche messen
...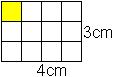 ... ... |
Will man in der Schule Flächeneinheiten einführen,
geht man z.B. von der linken Figur aus. Das gelbe Quadrat habe den Flächeninhalt
1 cm². Wie groß ist der Flächeninhalt des Rechtecks? |
Die Antwort 12 cm² erhält man über das Abzählen
der Einzelquadrate. Man kann auch zum Ergebnis über drei Balken
zu je vier Quadraten kommen. Das führt dann zu 3*4 cm² oder zur
Flächenformel A=ab.
Anzahl der
Rechtecke im Rechteck
...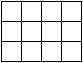 ... ... |
Es stellt sich die Frage, wie viele Rechtecke es unter
Verwendung des Gitters im 3x4-Rechteck gibt. |
Lösung

Ergebnis: Es gibt 60 Teilrechtecke.
Verallgemeinerung
In einem mxn-Rechteck gibt es (1/4)m(m+1)n(n+1) Rechtecke.
Quelle:
> Martin Wohlgemuth Zähle
Rechtecke in quadratischem Gitter (URL unten)
> Eric W. Weisstein (MathWorld) Rectangle Tiling
(URL unten)
Quadrate im
Rechteck
Die Zeichnungen oben zeigen, dass es leicht ist, ein
Rechteck aus Quadraten mit ganzzahligen Seiten zusammenzusetzen.
...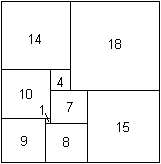 ... ... |
Es ist aber schwierig, ein Rechteck aus verschiedenen
Quadraten zu bilden.
Links wird das kleinste Rechteck (32x33) dargestellt,
für das das möglich ist.
Das ist wohl die erste Veröffentlichung:
R. Brooks, C. Smith, A. Stone, W. Tutte, The Dissection
of Rectangles into Squares, Duke Mathematics journal, 1940, Vol. 7, pp.
312-340. |
Mehr über dieses Problem erfährt
man über die Links unten.
Größte Rechtecke
top
Maße eines Sportplatzes
... ... ... |
Welche Maße muss ein Fußballplatz haben,
damit er eine Laufbahn
von a=400 m umschließt und möglichst groß
ist. |
Lösung
Zielfunktion: A=2xy
Nebenbedingung: a=2y+2pi*x oder y=(1/2)a-pi*x
Daraus folgt A(x)=2x[(1/2)a-pi*x]=ax-2pi*x² und
weiter A'(x)=a-4pi*x.
Ein Extremwert liegt evtl. vor, wenn A'(x)=0 ist. Das
heißt a-4pi*x=0 oder x=(1/4)a/pi.
Da A''(x)=-4pi , also kleiner als 0 ist, ist x=(1/4)a/pi
ein Maximum.
Dann ist y=(1/2)a-pi*x=(1/2)a-a/4=(1/4)a.
Ergebnis: Der Fußballplatz hat die Maße 2x=(1/2)a/pi
und y=(1/4)a.
Das führt zu den Zahlenwerten y=100m und 2x=63,7m.
Nach http://de.wikipedia.org/wiki/Fußballfeld#Spielfeld
sind
68 mal 105 Meter große Fußballplätze üblich.
Quadrat als
größtes Rechteck
Bei vielen Extremwertaufgaben sind Quadrate die größten
Rechtecke.
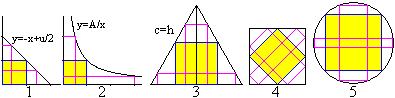 Mehr findet man auf meiner Quadrat-Seite.
Mehr findet man auf meiner Quadrat-Seite.
Aufteilung
eines Rechtecks top
Aufgabe: Teile ein Rechteck in vier flächengleiche
Teile.
Lösungen:

Schar von Rechtecken
top
Rechtecke gleichen Flächeninhalts
... ... ... |
Für Rechtecke gleichen Flächeninhalts gilt
xy
ist konstant oder xy=A oder y=A/x.
Das ist die Gleichung einer Hyperbel. |
Rechtecke gleichen
Umfangs
... ... ... |
Für Rechtecke gleichen Umfangs gilt 2x+2y ist
konstant oder 2x+2y=U oder y=-x+(1/2)U.
Das ist die Gleichung einer fallenden Geraden. |
Ähnliche
Rechtecke
... ... ... |
Die nebenstehenden Rechtecke haben die gleiche Form.
Sie sind ähnlich. |
... ... ... |
Schiebt man die Rechtecke nach unten links in eine perspektivische
Lage, so erkennt man nach dem ersten Strahlensatz, dass ähnliche Rechtecke
das gleiche Seitenverhältnis haben. |
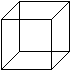
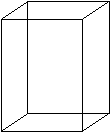
Quader
top
... ... ... |
Sechs geeignete Rechtecke bilden einen Körper, den
Quader.
Dieser Quader hat die Form eines Backsteins.
Das Normalformat eines Backsteins in Deutschland ist
24 cm × 11,5 cm× 7,1cm.
|
... ... ... |
Über weitere Quader, den Würfel
und das quadratische Prisma, gibt es gesonderte
Webseiten.
Zur
Definition des Rechtecks top
Oben wird das Rechteck definiert als ein Viereck, dessen
Winkel rechte Winkel sind.
Durch Anschauung findet man leicht die folgenden einfachen
Sätze zum Rechteck.
Satz 1: Alle Winkel sind gleich.
Satz 2: Je zwei Gegenseiten sind parallel.
Satz 3: Je zwei Gegenseiten sind gleich lang.
Satz 4: Die Diagonalen sind gleich lang.
Satz 5: Die Diagonalen halbieren sich.
Satz 6: Es gibt eine Symmetrieachse durch gegenüberliegende
Seitenmitten.
Definition
1
Die Definition des Rechtecks "Alle Winkel sind rechte
Winkel" wird durch den Namen bestimmt. Streng genommen ist diese Formulierung
ein Satz. Denn es genügt, nur drei rechte Winkel zu fordern. Aus dem
Satz, der besagt, dass die Winkelsumme im Viereck 360° ist, ergibt
sich der vierte Winkel auch zu 90°. Die Definition muss also heißen:
Ein Viereck wird zum Rechteck, wenn drei Winkel 90°
betragen.
Definition
2
Man könnte Satz 1 (Alle Winkel sind gleich.) auch
als Definition verwenden. Denn wieder ergeben sich über die Winkelsumme
drei bzw. vier Winkel von 90°.
Definition
3
Satz 4 und Satz 5 sind für sich genommen keine hinreichenden
Bedingungen für ein Rechteck, aber zusammen genommen schon.
... ... ...
|
Ein Viereck wird zum Rechteck, wenn die Diagonalen gleich
lang sind und sich halbieren. |
Es ist nicht zwingend vorgeschrieben,
welche Eigenschaft des Rechtecks man zu seiner Definition heranzieht. Bleibt
man bei Definition 1, so müssen die beiden anderen Definitionen zu
Sätzen erklärt und bewiesen werden.
Nehmen wir Definition 3 für weitere Überlegungen.
Definition 3 wird also zu Satz 7: Im Rechteck sind die
Diagonalen gleich lang und halbieren sich.
Satz 7 enthält zwei Aussagen, den Satz und den Kehrsatz:
(I)Wenn drei Winkel rechte Winkel sind, so sind die Diagonalen
gleich lang und halbieren sich.
(II)Wenn die Diagonalen gleich lang sind und sich halbieren,
so sind drei Winkel rechte Winkel.
(Die Beweise fehlen hier.)
Die beiden Richtungen drückt man auch durch folgende
Formulierungen aus:
Satz 7: Die Diagonalen sind in einem Viereck dann und
nur dann gleich lang und halbieren sich, wenn das Viereck ein Rechteck
ist.
Oder
Satz 7: Die Bedingung "Die Diagonalen sind gleich lang
und halbieren sich" ist notwendig und hinreichend für ein Rechteck.
Die Aussagen in Satz 2 bis Satz 6 sind nicht hinreichend,
aber notwendig. Sie gehören zum Rechteck.
Ist
das Quadrat ein Rechteck? top
... ... ... |
Das nebenstehende Viereck ist ein Quadrat.
Wenn man es als Rechteck bezeichnet, so erscheint die
Aussage falsch. |
Die Aussage ist aber mathematisch richtig. Alle Vierecke,
die drei rechte Winkel haben, heißen Rechtecke. Und das Quadrat hat
diese Eigenschaft. Also ist es „logisch“, dass das Quadrat ein Rechteck
ist.
... ... ... |
Dabei nimmt man in Kauf (siehe nächstes Kapitel),
dass man sich gegen eine landläufige Vorstellung stellt. Man erwartet,
dass ein Rechteck verschieden lange Seiten hat. So habe ich in einem Lexikon
die Formulierung gefunden: Im "eigentlichen" Rechteck sind die Seiten unterschiedlich
lang. - In alten Lehrbüchern findet man den Namen Oblong für
Rechtecke mit verschieden langen Seiten. Dann erfasst das Rechteck Quadrat
und Oblong. |
... ... ... |
Natürlich erwartet man, dass die Figur nicht als
Rechteck, sondern als Quadrat bezeichnet wird. Offenbar muss man immer
einen Namen angeben, der alle Eigenschaften des Vierecks erfasst. |
Hier passt ein Irrtum der
Redakteure hinter Günther Jauchs „Wer wird Millionär?“ vor einigen
Jahren.
Die Frage hieß: Jedes Rechteck ist ein...? A: Rhombus
B: Quadrat C: Trapez D: Parallelogramm
Erwartet wurde als Antwort Parallelogramm. Das
ist richtig, aber Trapez ist auch eine Antwort. Das Rechteck hat
nämlich wie das Trapez ein Paar paralleler Seiten.
Bei de.wikpedia steht eine
mögliche Erklärung für den Irrtum: Die Quelle war veraltet.
Da ich noch einen Brockhaus von 1975 besitze, kann ich zitieren: (Das Trapez
ist ein) "Viereck mit zwei gleichlaufenden, aber ungleich langen Seiten."
Das Quadrat
ist ein Rechteck top
Bliebe noch zu klären, warum es sinnvoll ist, das
Quadrat als Spezialfall eines Rechtecks zu definieren.
Angenommen, man definiere das Rechteck wie folgt.
Definition: Ein Viereck wird zum Rechteck, wenn drei
Winkel 90° betragen und wenn die Seiten verschieden lang sind. Dann
könnte man zwar die Sätze 1 bis 6 einfach übernehmen, nicht
aber Satz 7.
Satz 7 lautete: Die Diagonalen sind in einem Viereck
dann und nur dann gleich lang und halbieren sich, wenn das Viereck ein
Rechteck ist.
Der Kehrsatz "Wenn die Diagonalen gleich lang sind und
sich halbieren, so ist das Viereck ein Rechteck" gilt nicht mehr. Auch
das Quadrat hat diese Eigenschaft.
Satz 7 wird wieder richtig, wenn man ihn so formuliert.
Satz 7': Die Diagonalen sind in einem Viereck dann und
nur dann gleich lang und halbieren sich und die Seiten sind verschieden
lang, wenn das Viereck ein Rechteck ist.
An diesem Beispiel sieht man, wie umständlich die
Sätze werden. Grundsätzlich kann man natürlich für
das Rechteck verschieden lange Seiten fordern. Aber man muss die zusätzliche
Eigenschaft mitschleppen. Es ist viel einfacher, das Quadrat mit einzubeziehen
und es als Spezialfall zu betrachten.
In diesem Zusammenhang ist
das Parallelenproblem berühmt.
Bekanntlich schneiden sich zwei Geraden in einem Punkt
oder, wenn sie parallel sind, in keinem Punkt.
Nun gibt es einen Ansatz mit der Aussage: Zwei
Geraden schneiden sich immer in einem Punkt. Damit man sich das vorstellen
kann, ordnet man auch den Parallelen genau einen Schnittpunkt zu, und konkret
ist das ein Punkt, der "im Unendlichen" liegt und der der Richtung einer
Geraden zugeordnet wird. Mit diesem Ansatz kann man die sogenannte Projektive
Geometrie
entwickeln, die viele Sätze im Zusammenhang mit sich
schneidenden Geraden in eleganter Weise liefert. Sätze über Parallelen
erscheinen als Spezialfälle.
Weitere Seiten
top
Noch mehr über Rechtecke findet man an anderen Stellen
meiner Homepage.
Pentominos
Rechteck im Internet
top
Deutsch
Arndt Brünner
Nullstellen
(Lösungen) von Polynomen bestimmen
Eckard Specht
MATH4U.DE
W.1 Lage der Mittelpunkte von Umkreisen
Jürgen Ullwer (mathe-trainer.de)
Flächenverwandlung
mit Hilfe des Höhensatzes, Flächenverwandlung
mit Hilfe des Kathetensatzes
Martin Wohlgemuth
Zähle
Rechtecke in quadratischem Gitter
Wikipedia
Rechteck,
Quadratur
des Rechtecks, Seitenverhältnis
(Film)
Englisch
Alexander Bogomolny (cut-the-knot)
Dissection
of a Rectangle into Two Chessboards, Equidecomposition
of a Triangle and a Rectangle II,
Rectangle
in Arbelos, Two
Rectangles in a Rectangle, Squaring
a Rectangle, Circles
and Semicircles in Rectangle,
Orthocentric
System From Rectangle
Antonio Gutierrez
The
Golden Rectangle and Machu Picchu
David Broughton
RECTANGLE
IN A RECTANGLE
Eric W. Weisstein (MathWorld)
Rectangle,
Golden
Rectangle,
Blanches
Dissection, Fault-Free
Rectangle, Perfect
Rectangle, Rectangle
Tiling, Rectangle
Squaring, Rounded
Rectangle, Mrs
Perkins's Quilt
Tweedledum (Bill's Graphics)
Rectangles
divided into (mostly) unequal squares
Wikipedia
Rectangle,
Golden
rectangle,
Root
rectangle, Squaring
the square, Oblong,
Aspect
ratio
Referenzen top
Lothar Kusch, Mathematik für Schule und Beruf, Teil
2, Essen 1971 [ISBN 3 7736 2582 0]
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2008 Jürgen Köller
top |




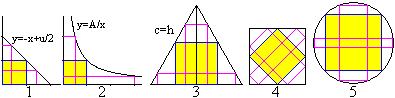

 ...
... ...
... ...
... .
.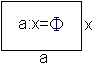 ...
...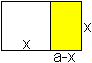 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...