|
Was sind Kreise in einer Figur?
Vor zehn Jahren (2003) erstellte ich eine Webseite zum
Thema Kreise im Kreis. Schon damals
plante ich eine weitere Webseite, in der Kreise in anderen einfachen Figuren
wie im gleichseitigen Dreieck oder im Quadrat untersucht werden. Hier ist
nun die Seite.
Kreise
im Kreis top
Bei diesem Thema verweise ich auf
meine Webseite
Kreise im Kreis. Dort
findet man u.a. die folgenden Figuren.
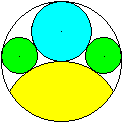
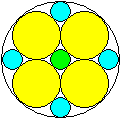
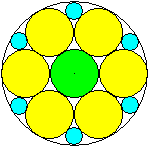
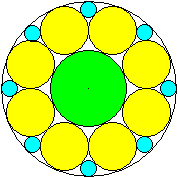
Sieben Kreise im Kreis
...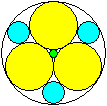 ... ... |
In den Formeln ist
R der Radius des Umkreises
r der Radius eines (gelben) Kreises
x der Radius eines (blauen) Lückenkreises
y der Radius des (grünen) Zentralkreises |
r=[2sqrt(3)-3]R
x=(1/11)[2sqrt(3)-1]R
y=[7-4sqrt(3)]R |
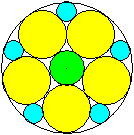
Fünf
Kreise in Kreis
...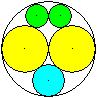 ... ... |
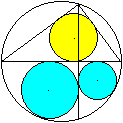
Legt man in einen Kreis zwei (gelbe) Kreise nebeneinander,
so ist Platz für drei weitere Kreise.
Ist R der Radius des großen
Kreises, r der Radius eines gelben Kreises, x des blauen und y eines grünen
Kreises, so gilt
r=(1/2)R, x=(1/3)R und y=(1/4)R.
Die
Durchmesser der vier verschiedenen Kreise stehen im Verhältnis 12:6:4:3. |
Ringe
aus Kreisen im Kreis
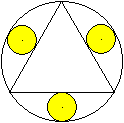
Drei
Kreise im Umkreis 1
... ... ...
|
Legt man um ein gleichseitiges Dreieck den Umkreis, so
ist Platz für drei weitere gleiche Kreise.
Die Kreise berühren den Umkreis innen und das Dreieck
außen.
Ist die Seitenlänge a des Dreiecks gegeben, so hat
ein Kreis den Radius r=(1/12)sqrt(3)a. |
Drei
Kreise im Umkreis 2
... |
|
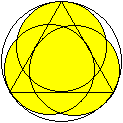
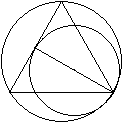
Legt man um ein gleichseitiges Dreieck einen Umkreis,
so ist Platz für drei weitere gleiche Kreise.
Die Kreise berühren den Umkreis und das Dreieck innen.
Ist die Seitenlänge a des Dreiecks gegeben, so hat
ein Kreis den Radius r=(1/4)sqrt(3)a. |
Vier
Kreise im Umkreis
...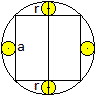 ... ... |
Für den Durchmesser des Umkreises gilt sqrt(2)a
= a+4r.
Daraus folgt r=(1/4)[sqrt(2)-1]a. |
Soddy-Kreise
Mehr auf der Webseite Soddy Circles von MathWorld
(URL unten)
Zehn
Kreise im Dreieck top
...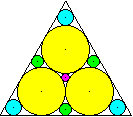 ... ... |
Gegeben sei ein gleichseitiges Dreieck mit der Seitenlänge
a mit 10 sich berührenden Kreisen im Inneren.
Gesucht sind die Radien der Kreise. |
Lösungen
Drei große Kreise
...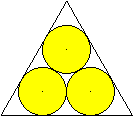 ... ... |
...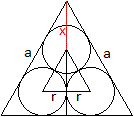 ... ... |
Gegeben sei die Seitenlänge a des umfassenden Dreiecks,
gesucht ist der Radius r eines Innenkreises.
Verbindet man die Mittelpunkte der Kreise, so entsteht
ein gleichseitiges Dreieck mit der Seite 2r, der Höhe h=sqrt(3)r und
dem Radius des Umkreises R=(2/3)sqrt(3)r. - Das gleichseitige Dreieck hat
die Höhe h'=(1/2)sqrt(3)a und den Radius des Umkreises R'=(1/3)sqrt(3)a.
Dann gilt h'=r+sqrt(3)r+x und x=R'-R=(1/3)sqrt(3)a-(2/3)sqrt(3)r.
Weiter gilt
(1/2)sqrt(3)a=r+sqrt(3)r+(1/3)sqrt(3)a-(2/3)sqrt(3)r.
Das führt zu r=(1/4)[sqrt(3)-1]a. |
Drei
Kreise in den Ecken
...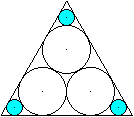 ... ... |
...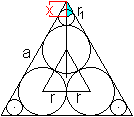 ... ... |
Gegeben sei die Seitenlänge a des umfassenden Dreiecks,
gesucht ist der Radius r eines Innenkreises an der Spitze.
Verbindet man die Mittelpunkte der großen Kreise,
so entsteht ein gleichseitiges Dreieck mit der Seite 2r, der Höhe
h=(1/2)sqrt(3)(2r) und dem Radius des Umkreises Ra=(2/3)[(1/2)sqrt(3)2r]. |
Der Radius des Umkreises des Dreiecks mit der Seitenlänge
a (nicht eingezeichnet) setzt sich aus vier Teilstrecken zusammen.
(2/3)[(1/2)sqrt(3)a] = Ra+r+r1+x
oder (1/3)sqrt(3)a= (2/3)sqrt(3)r+r+r1+x, wobei r=(1/4)[sqrt(3)-1]a
ist und im blauen Dreieck sin(30grad)=r1/x gilt. - Nach einigen
Rechenschritten erhält man r1=(1/12)[sqrt(3)-1]a.
Drei
Kreise in den Seitenmitten
...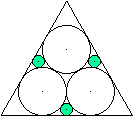 ... ... |
...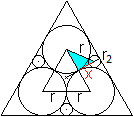 ... ... |
Gegeben sei die Seitenlänge a des umfassenden Dreiecks,
gesucht ist der Radius r eines Innenkreises an der Seitenmitte.
Verbindet man die Mittelpunkte der großen Kreise,
so entsteht im Inneren ein gleichseitiges Dreieck mit der Seite 2r, der
Höhe h=(1/2)sqrt(3)(2r) und dem Radius des Inkreises Ri=(1/3)[(1/2)sqrt(3)2r]. |
Der Radius des Inkreises des Dreiecks mit der Seite a
(nicht eingezeichnet) setzt sich aus drei Teilstrecken zusammen.
(1/3)[(1/2)sqrt(3)a] = Ri+x+r2
oder (*) (1/6)sqrt(3)a= (1/3)sqrt(3)r+x+r2, wobei r=(1/4)[sqrt(3)-1]a
gilt.
Im blauen Dreieck gilt nach dem Satz des Pythagoras (**)
(r+r2)²=x²+r².
Die Gleichungen (*) und (**) enthalten die Suchvariablen
x und r2.
Nach längerer Rechnung erhält man r2=(1/16)[sqrt(3)-1]a.
Ein
Kreis in der Mitte
...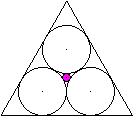 ... ... |
...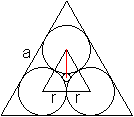 ... ... |
Gegeben sei die Seitenlänge a des umfassenden Dreiecks,
gesucht ist der Radius r des kleinen Kreises in der Mitte.
Verbindet man die Mittelpunkte der großen Kreise,
so entsteht ein gleichseitiges Dreieck mit der Seite 2r, der Höhe
h=(1/2)sqrt(3)(2r) und dem Radius des Umkreises Ra=(2/3)[(1/2)sqrt(3)2r]. |
Der Radius des Umkreises des kleinen Dreiecks (nicht eingezeichnet)
setzt sich aus zwei Teilstrecken zusammen.
(2/3)[(1/2)sqrt(3)2r] = r+r3, wobei r=(1/4)[sqrt(3)-1]a
ist.
Nach längerer Rechnung erhält man r3=(1/12)[9-5sqrt(3)]a.
... ... ... |
Es ist bemerkenswert, dass sich die Radien der ersten
drei Kreise in ganzen Zahlen verhalten, r : r1 :
r2=12
:
4
:
3. |
Es folgt ein Screenshot des
passenden Geogebra-Programms, geschrieben von Peter Katzlinger und mir
freundlicherweise zur Verfügung gestellt.
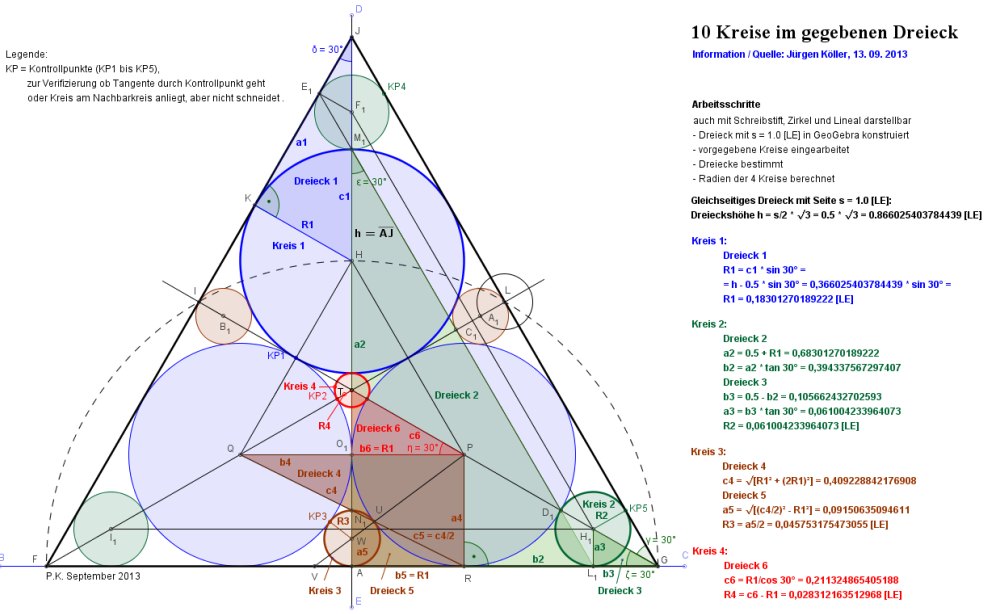
Das ist das zugehörige Programm.
Es benötigt das Java Runtime Environment (JRE), das man erhält,
wenn man Geogebra als (freie) Software installiert. Das Besondere ist,
dass man sich die einzelnen Schritte zum Erstellen der Zeichnung anzeigen
lassen kann. Dazu geht man unten rechts auf das Feld Abspielen.
Vorher sollte man die Größe der Zeichnung mit dem Mausrädchen
dem Bildschirm anpassen.
Weitere Kreise
im Dreieck top
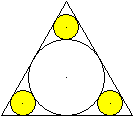
Inkreis und drei Kreise in den
Ecken
... ... ... |
...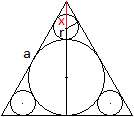 ... ... |
Der Höhe des Dreiecks mit der Seitenlänge a
setzt sich aus drei Teilstrecken zusammen, nämlich dem Durchmesser
des Inkreises, dem gesuchten Radius des Kreises an der Spitze und der Strecke
x.
Es gilt sin(30°)=r/x oder x=2r.
Das heißt (1/2)(sqrt(3)a=2*(1/3)[(1/2)sqrt(3)a]+3r.
Nach einigen Rechenschritten erhält man r=(1/18)sqrt(3)a. |
Malfatti
Problem
... ... ... |
... ... ... |
...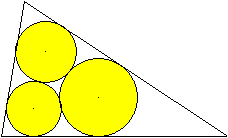 ...: ...: |
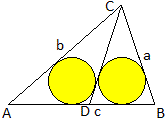
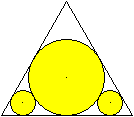
Drei Kreise in einem beliebigen Dreieck, die sich außen
und die Dreiecksseiten innen berühren, heißen Malfatti-Kreise. |
... ... ... |
Der italienische Mathematiker Gianfrancesco Malfatti
(1731 bis 1807) hat sich nämlich mit dem Problem beschäftigt,
ein beliebiges Dreieck mit drei Kreisen so auszufüllen, dass sie zusammen
einen möglichst großen Flächeninhalt bilden.
Das Problem ist rechnerisch und zeichnerisch gelöst.
Diese Zeichnung und Näheres findet man auf der Webseite
Malfatti's
Problem bei Mathworld (URL unten). |
Ist das Dreieck gleichseitig,
so gibt es einfache Lösungen.

72,9 %
|

73,9 %
|
Links stehen die Lösungen für den Fall gleicher
Kreise und für den Fall verschiedener Kreise.
Quelle: http://en.wikipedia.org/wiki/Malfatti_circles
Die Prozentzahlen geben den Anteil der Kreise an der Dreiecksfläche
an. |
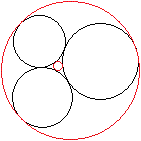
Ein
Dreieck und 17 Kreise
...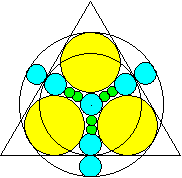 ... ... |
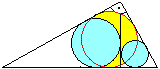
Gegeben sei der Radius c eines grünen Kreises.
Gesucht sind der Radius R des großen Kreises, des
Inkreises des Dreiecks r, eines gelben Kreises a und eines blauen Kreises
b.
Man liest unmittelbar ab: a+b = 2b+4c, r = 3b+4c, R =
5b+4c, R = b+2a
Daraus ergibt sich a=6c, b=2c, r=10c
und R=14c.
Quelle: Alexander Bogomolny, Problem11: Sangaku by a teen
(URL unten) |
Neun
Kreise im Quadrat top
...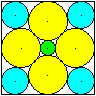 ... ... |
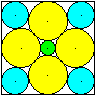
Gegeben sind neun Kreise in einem Quadrat der Seitenlänge
a. .........................................................
Gesucht sind ihre Radien. |
Lösung
Vier große Kreise
... ... ... |
...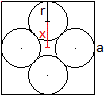 ... ... |
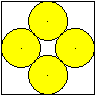
Gegeben sei die Seite a des Quadrates, gesucht ist der
Radius r eines Kreises.
Es gilt (1/2)a=x+r mit x=sqrt(2)r. Dann ist (1/2)a=sqrt(2)r+r
oder r=(1/2)[sqrt(2)-1]a. |
Vier
Kreise in den Ecken
... ... ... |
...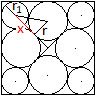 ... ... |
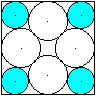
Gegeben sei die Seite a des Quadrates, gesucht ist der
Radius r1 eines Kreises in der Ecke.
Es gilt (1/2)sqrt(2)a=r+x+sqrt(2)r1, wobei
(r1+r)²=x²+r² und r=(1/2)[sqrt(2)-1]a ist.
Nach langer Rechnung ergibt sich r1={(1/2)[2sqrt(2)-1]-sqrt[2-sqrt(2)]}a. |
Ein
Kreis in der Mitte
... ... ... |
... ... ... |
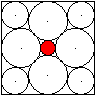
Gegeben sei die Seite a des Quadrates, gesucht ist der
Radius r2 des Kreises in der Mitte.
Es gilt r+r2 = sqrt(2)r mit r=(1/2)[sqrt(2)-1]a.
Nach einigen Rechenschritten ergibt sich r2=(1/2)[3-2sqrt(2)]a. |
Es folgt noch ein Screenshot
eines weiteren Geogebra-Programms, auch zur Verfügung gestellt von
Peter Katzlinger.
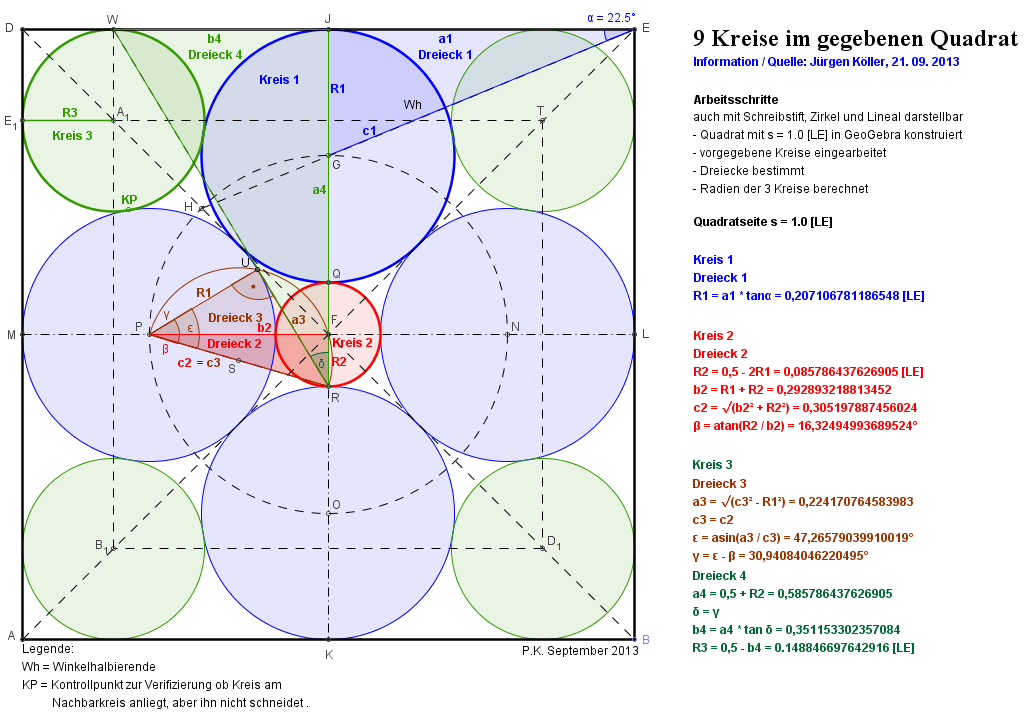
Das ist das zugehörige Programm.
Weitere Kreise
im Quadrat top
Drei gleiche Kreise im Quadrat
... |
...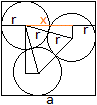 ... ... |
Gegeben sei der Radius r eines Innenkreises, gesucht
ist die Seitenlänge des umfassenden Quadrats.
Verbindet man die Mittelpunkte der Kreise, so entsteht
ein gleichseitiges Dreieck mit der Seite 2r.
Man errichtet über zwei Seiten je ein rechtwinkliges
Dreieck mit einer zur Seite des Quadrates parallelen Kathete x. Diese Dreiecke
haben die spitzen Winkel 15° und 75°.
Dann gilt a = r+x+r = 2r+2rcos(15°) = 2r+2r(1/4)[sqrt(6)+sqrt(2)]
oder a = [2+(1/2)sqrt(2)+(1/2)sqrt(6)]r. |
Fünf
Kreise im Quadrat
... ... ... |
...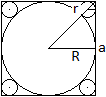 ... ... |
Gegeben sei die Seite a des Quadrates, gesucht ist der
Radius eines Kreises in der Ecke.
Der große Kreis hat den Radius R=(1/2)a.
Für den Radius r eines kleinen Kreises gilt (1/2)sqrt(2)a=R+r+sqrt(2)a.
Nach etlichen Rechenschritten ergibt sich r = (1/2)[3-2sqrt(2)]a. |
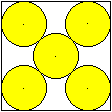
Fünf
gleiche Kreise im Quadrat 1
... ... ... |
 ... ...
|
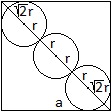
Gegeben sei die Seite a des Quadrates, gesucht ist der
Radius eines Kreises.
Es gilt 2sqrt(2)r+4r=sqrt(2)a oder r=(1/2)[sqrt(2)-1)]a. |
Fünf
gleiche Kreise im Quadrat 2
...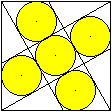 ... ... |
Es gibt eine interessantere Variante der letzten Aufgabe.
Da gilt die Formel r=(1/4)[sqrt(3)-1)]a.
Die Aufgabenstellung und Lösung findet man unten
unter "sangaku - a geometrical puzzle" bei Mathematics
Stack Exchange (URL unten). |
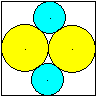
Zwei
Kreispaare in Quadrat 1
... |
|
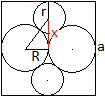
Gegeben sei die Seite a des Quadrates, gesucht sind die
Radien der Kreise.
Es gilt für den gelben R = (1/4)a.
Nach dem Satz des Pythagoras gilt (R+r)² = x²+R².
Weiter ist (1/2)a = x+r.
Nach einigen Rechenschritten ergibt sich für den
blauen Kreis r = (1/6)a. |
Zwei
Kreispaare in Quadrat 2
... ... ... |
Gegeben sei die Seite a des Quadrates.
Gesucht sind die Radien R und r der Kreise. ......................................................................... |
...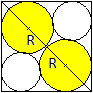 ... ... |
Für die Diagonale des Quadrats gilt sqrt(2)a = 2R*sqrt(2)+2R.
Nach einigen Rechenschritten ergibt sich R = (1/2)[2-sqrt(2)]a....................... |
...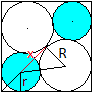 ... ... |
Für die halbe Diagonale gilt (1/2)sqrt(2)a = sqrt(2)r+x.
Nach dem Satz des Pythagoras gilt (R+r)² = R²+x².
Man setzt R = (1/2)[2-sqrt(2)]a ein und erhält 2
Gleichungen in den Variablen x und r.
Nach etlichen Rechenschritten ergibt sich r={2-(1/2)sqrt(2)-sqrt[4-2sqrt(2)]}a
oder gerundet 0,211a. |
Kreis
einpassen 1
... 0... 0... |
Gegeben seien ein Quadrat der Seitenlänge a und
fünf Kreise mit dem Radius r=(1/6)a, die sich und zwei nebeneinander
liegende Seiten des Quadrates innen berühren.
Gesucht ist der Radius R des Kreises, der vier Kreise
und die freien Seiten des Quadrates innen berührt. |
...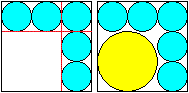 ... ... |
Zeichnet man die gemeinsamen Tangenten zu je drei Kreisen,
so wird ein Quadrat gebildet.
Der Inkreis des Quadrates hat einen Radius von (1/3)a.
So hat man einen Anhaltspunkt: Der gesuchte Kreis muss
einen etwas größeren Radius haben. |
...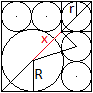 ... ... |
Ergänzt und beschriftet man die Zeichnung wie links,
so kann man zwei Gleichungen ablesen.
Für die Diagonale gilt sqrt(2)a = sqrt(2)R+x+2sqrt(2)r.
Nach dem Satz des Pythagoras gilt (R+r)² = x²+[sqrt(2)r]².
Man setzt r=(1/6)a und man erhält 2 Gleichungen
in den Variablen x und R. |
Nach längerer Rechnung erhält
man R=(1/6)[9-4sqrt(3)]a. Das ist gerundet R=0,345a, also ein wenig
größer als (1/3)a.
Kreis einpassen 2
...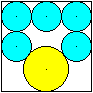 ... ... |
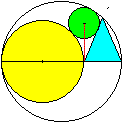
Das Problem wird einfacher, wenn man die fünf Kreise
wie links vorgibt.
Wie eine Rechnung bestätigt, hat der untere Kreis
den Radius R=(1/4)a, wenn die Länge des Quadrates a ist. |
13
Kreise im Quadrat
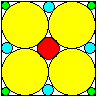
...
|
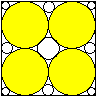
r=(1/4)a
|
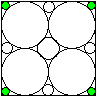
r1=(1/4)[3-2sqrt(2)]a
|
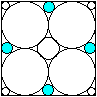
r2=(1/16)a
|
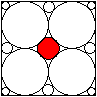
r3=(1/4)[sqrt(2)-1]a
|
Zur Herleitung der Formeln
Die bisherigen Rechnungen auf dieser Seite erfolgten
auf gleichen Wegen: Man zerlegt den Radius eines In- oder Umkreises in
Streckenabschnitte. Eine Teilstrecke x wird dann nach dem Satz des Pythagoras
bestimmt.
Auf diese Darstellung verzichte ich in dieser Aufgabenfolge.
Auf meiner Webseite Sangaku-Figuren
findet man mehr zum Thema.
Kreise
in einer Figur im Internet top
Deutsch
Wikipedia
Satz
von Descartes, Malfatti-Kreis,
Ford-Kreis,
Wasan
Englisch
Alexander Bogomolny (Cut-the Knot)
Malfatti's
Problem, Soddy
Circles and David Eppstein's Centers: What Are They?, 11
Sangaku by a teen
Eric W. Weisstein (MathWorld)
Malfatti
Circles, Malfatti's
Problem, Marble
Problem, Circle-Circle
Intersection, ReuleauxTriangle,
Monge's
Circle Theorem,
Tangent
Circles, Johnson
Circles, Circle
Packing, Soddy
Circles, Casey's
Theorem
Mathematics Stack Exchange
sangaku
- a geometrical puzzle (http://math.stackexchange.com/questions/4480/sangaku-a-geometrical-puzzle)
Wikipedia
Descartes'
theorem, Malfatti
circles, Circle
packing in a square,
Ford
circle
Feedback: Emailadresse auf meiner Hauptseite
URL meiner Homepage:
https://www.mathematische-basteleien.de/
© 2013 Jürgen Köller
top |




 ...
...
 ...
...

 ...
...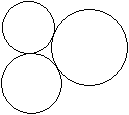 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...:
...: ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...
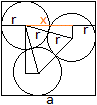 ...
... ...
... ...
... ...
... ...
... ...
...

 ...
... ...
... ...
... 0...
0... ...
... ...
... ...
...