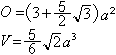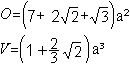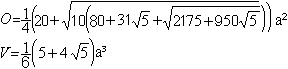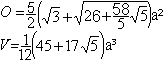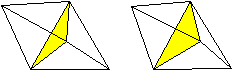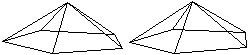|
Die Kuppeln unter den Johnson-Körpern
|
Was ist eine Kuppel?
... ... ... |
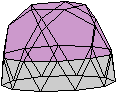
Im landläufigen Verständnis ist eine Kuppel
eine Halbkugel, die einen Raum oben abschließt.
Auf dieser Seite ist die Kuppel ein von regelmäßigen
Vielecken gebildeter mathematischer Körper, der wie eine Kuppel aussieht. |
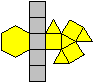
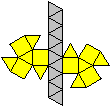
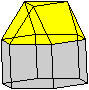
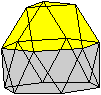
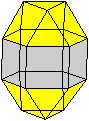
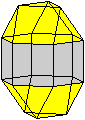
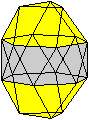
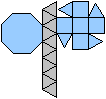
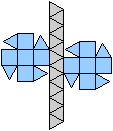
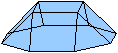
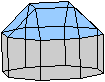
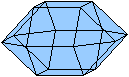
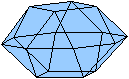
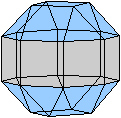
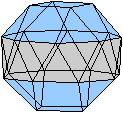
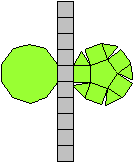
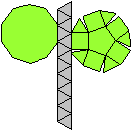
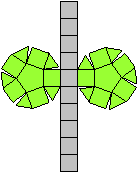
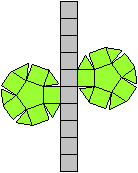
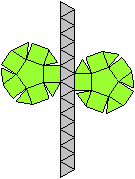
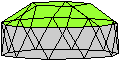
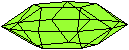
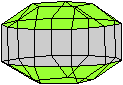
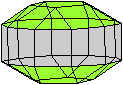
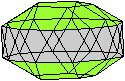
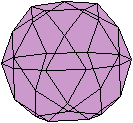
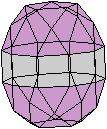
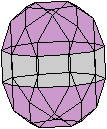
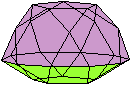
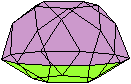
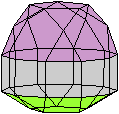
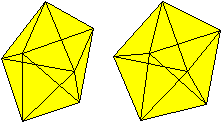
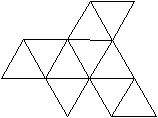
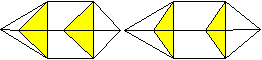
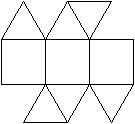
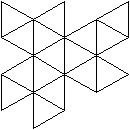
Es folgen die Bilder einfacher Körper dieser Art. Das
sind die Dreieckskuppel, die Quadratkuppel und die Fünfeckskuppel.
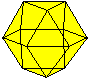
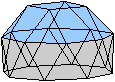
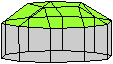
Der vierte Körper rechts heißt wohl auch wegen der aufwändig
gestalteten Kuppel Rotunde, genauer Fünfecksrotunde.
So kann man zwei Körper mit gleicher Deckfläche voneinander unterscheiden.
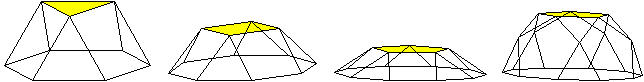
Was ist ein Johnson-Körper?
Neben den fünf platonischen
Körpern und den 13 archimedischen Körpern
gibt es noch beliebig viele konvexe Körper, die von regelmäßigen
Vielecken begrenzt werden, die Prismen und die
Antiprismen.
Die restlichen konvexen Körper aus regelmäßigen
Vielecken sind die 92 Johnson-Körper.
Von ihnen werden auf dieser Seite die 34 Körper
vorgestellt, die Kuppeln sind oder die auf die vier oben vorgestellten
Grundkörper zurückgeführt werden können.
Dreieckskuppel
top
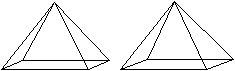
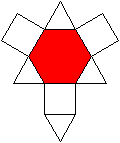
Die Dreieckskuppel hat ein Sechseck
als Grundfläche und ein Dreieck als Deckfläche. Die Fläche
dazwischen besteht aus drei Dreiecken und drei Quadraten. Das zeigen die
folgenden Ansichten in 3D.
... ... ... |
...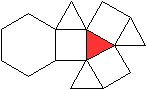 ... ... |
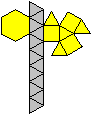
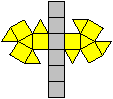
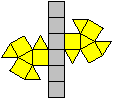
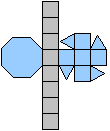
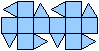
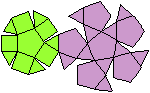
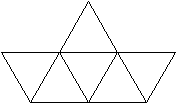
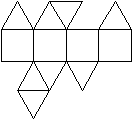
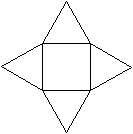
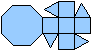
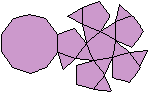
Ein Netz kann man so anlegen, dass entweder die Grundfläche
oder die Deckfläche isoliert ist. |
...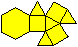 ... ... |
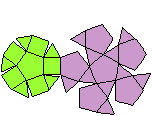
Bei den folgenden Kuppel-Darstellungen bevorzuge ich
die, die die Kuppeln gut veranschaulichen und die Grundflächen isoliert
zeigen. |
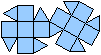
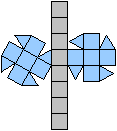
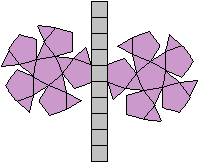
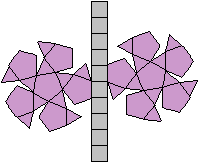
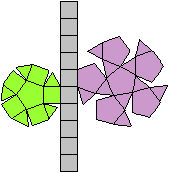
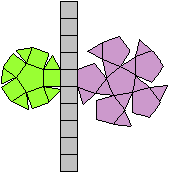
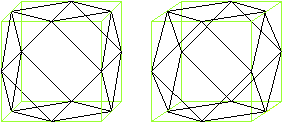
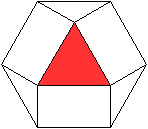
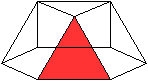
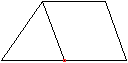
Es gibt besondere, in der
Ebene symmetrische Ansichten der Dreieckskuppel. Die rot gezeichneten Elemente
liegen vorne.
... ... ...
|
Die Dreieckskuppel ist ein halbes Kuboktaeder,
das in der Sechseck-Ebene halbiert wird. |
Quadratkuppel
top
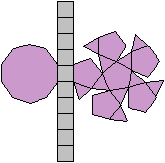
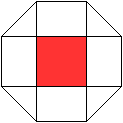
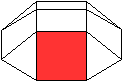
Die Quadratkuppel hat ein Achteck
als Grundfläche und ein Quadrat als Deckfläche. Die Fläche
dazwischen besteht aus vier Dreiecken und vier Quadraten.
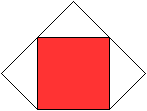
Es gibt besondere, in der Ebene symmetrische Ansichten
der Quadratkuppel. Die rot gezeichneten Elemente liegen vorne.
Fünfeckskuppel
top
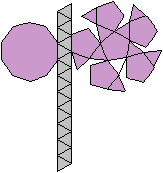
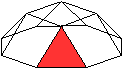
Die Fünfeckskuppel hat ein
Zehneck als Grundfläche und ein Fünfeck als Deckfläche.
Die Fläche dazwischen besteht aus fünf Dreiecken und fünf
Quadraten.
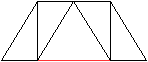
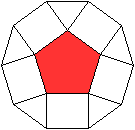
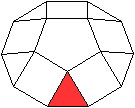
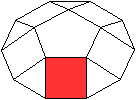
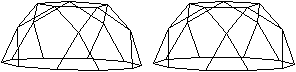
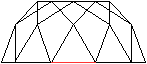
Es gibt besondere, in der
Ebene symmetrische Ansichten der Fünfeckkuppel.
Die rot gezeichneten Elemente liegen vorne.
Fünfecksrotunde
top
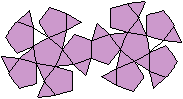
Die Fünfecksrotunde hat ein
Zehneck als Grundfläche und ein Fünfeck als Deckfläche.
Die Fläche dazwischen besteht aus fünf Fünfecken und 10
Dreiecken, die paarweise, Spitze an Spitze, zwischen den Fünfecken
liegen.
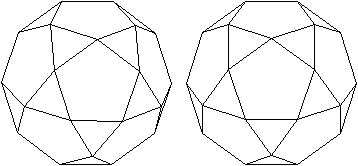
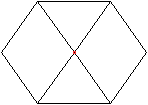
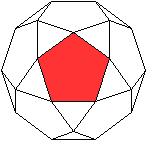
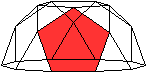
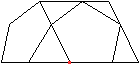
Es gibt besondere, in der
Ebene symmetrische Ansichten der Fünfecksrotunde.
Die rot gezeichneten Elemente liegen vorne.
... ... ...
|
Die Dreieckskuppel ist ein halbes Ikosidodekaeder,
das in der Zehneck-Ebene halbiert wird. |
Die folgenden Daten findet man bei MathWorld bzw. WolframAlpha.
- Gegeben sei jeweils die Kante a.
Dreieckskuppel
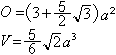
gerundet:
O=7,33a², V=1,18a³ |
Quadratkuppel
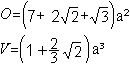
gerundet:
O=11,56a², V=1,94a³ |
Fünfeckskuppel
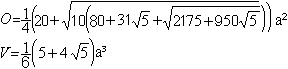
gerundet:
O=16,58a², V=2,32a³ |
Fünfecksrotunde
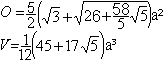
gerundet:
O=22,36a², V=6,92a³ |
Ordnen der Kuppeln
top
Sieben Körper gehen aus der Dreieckskuppel hervor.
|
J3
|
J18
|
J22
|
J27
|
J35
J36
|
J44
|
Beschreibung
J3 ist die Dreieckskuppel.
J18: Zwischen der Grundfläche und dem Mantel der
Kuppel liegt ein Ring aus Quadraten.
J22: Zwischen der Grundfläche und dem Mantel der
Kuppel liegt ein Ring aus gleichseitigen Dreiecken.
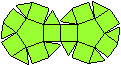
J27: Zwei Dreieckskuppeln bilden eine Doppelkuppel.
J35: Zwischen den beiden Dreieckskuppeln liegt ein Ring
aus Quadraten.
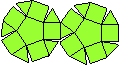
J36: Die beiden Kuppeln sind gegeneinander gedreht.
J44: Zwischen den beiden Dreieckskuppeln liegt ein Ring
aus gleichseitigen Dreiecken.
Sieben Körper gehen aus der Quadratkuppel
hervor.
|
J4
|
J19
|
J23
|
J28
J29
|
J37
|
J45
|
Acht Körper gehen aus
der Fünfeckskuppel hervor.
|
J5
|
J20
|
J24
|
J30
J31
|
J38
J39
|
J46
|
Sieben Körper gehen
aus der Fünfecksrotunde hervor.
J48
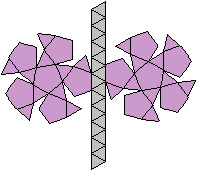
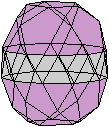
Fünf Körper sind
eine Kombination von Fünfeckskuppel und Fünfecksrotunde.
Das sind zusammen 7+7+8+7+5=34 Körper.
Namen top
Der Name einer Kuppel ist so gewählt, dass er den
Körper gut beschreibt.
J03 Dreieckskuppel
J04 Quadratkuppel
J05 Fünfeckskuppel
J06 Fünfecksrotunde
J18 verlängerte Dreieckskuppel
J19 verlängerte Quadratkuppel
(beschnittenes kleines
Rohmbenkuboktaeder)
J20 verlängerte Fünfeckskuppel
J21 verlängerte Fünfecksrotunde
J22 verdreht verlängerte Dreieckskuppel
J23 verdreht verlängerte Quadratkuppel
J24 verdreht verlängerte Fünfeckskuppel
J25 verdreht verlängerte Fünfecksrotunde
J27 Dreiecksdoppelkuppel
(verdrehtes Kuboktaeder)
J28 Quadratdoppelkuppel
J29 verdrehte Quadratdoppelkuppel
J30 Fünfecksdoppelkuppel
J31 verdrehte Fünfecksdoppelkuppel
J32 Fünfeckskuppelrotunde
J33 verdrehte Fünfeckskuppelrotunde
J34 Fünfecksdoppelrotunde
(verdrehtes Ikosidodekaeder)
J35 verlängerte Dreiecksdoppelkuppel
J36 verlängerte verdrehte Dreiecksdoppelkuppel
J37 verlängerte verdrehte Quadratsdoppelkuppel
(verdrehtes kleines
Rhombenkuboktaeder)
J38 verlängerte Fünfecksdoppelkuppel
J39 verlängerte verdrehte Fünfecksdoppelkuppel
J40 verlängerte Fünfeckskuppelrotunde
J41 verlängerte verdrehte Fünfeckskuppelrotunde
J42 verlängerte Fünfecksdoppelrotunde
J43 verlängerte verdrehte Fünfecksdoppelrotunde
J44 verdreht verlängerte Dreiecksdoppelkuppel
J45 verdreht verlängerte Quadratdoppelkuppel
J46 verdreht verlängerte Fünfecksdoppelkuppel
J47 verdreht verlängerte Fünfeckskuppelrotunde
J48 verdreht verlängerte Fünfecksdoppelrotunde
J91 Bilunadoppelrotunde
J92 Dreieckshebosphenorotunde |
J03 Triangular cupola
J04 Square cupola
J05 Pentagonal cupola
J06 Pentagonal rotunda
J18 Elongated triangular cupola
J19 Elongated square cupola
(diminished rhombicuboctahedron)
J20 Elongated pentagonal cupola
J21 Elongated pentagonal rotunda
J22 Gyroelongated triangular cupola
J23 Gyroelongated square cupola
J24 Gyroelongated pentagonal cupola
J25 Gyroelongated pentagonal rotunda
J27 Triangular orthobicupola
(gyrate cuboctahedron)
J28 Square orthobicupola
J29 Square gyrobicupola
J30 Pentagonal orthobicupola
J31 Pentagonal gyrobicupola
J32 Pentagonal orthocupolarotunda
J33 Pentagonal gyrocupolarotunda
J34 Pentagonal orthobirotunda
(gyrate icosidodecahedron)
J35 Elongated triangular orthobicupola
J36 Elongated triangular gyrobicupola
J37 Elongated square gyrobicupola
(gyrate rhombicuboctahedron)
J38 Elongated pentagonal orthobicupola
J39 Elongated pentagonal gyrobicupola
J40 Elongated pentagonal orthocupolarotunda
J41 Elongated pentagonal gyrocupolarotunda
J42 Elongated pentagonal orthobirotunda
J43 Elongated pentagonal gyrobirotunda
J44 Gyroelongated triangular bicupola
J45 Gyroelongated square bicupola
J46 Gyroelongated pentagonal bicupola
J47 Gyroelongated pentagonal cupolarotunda
J48 Gyroelongated pentagonal birotunda
J91 Bilunabirotunda
J92 Triangular hebesphenorotunda |
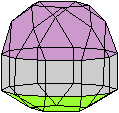
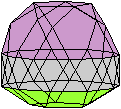
J91 und J92
top
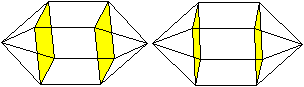
Die beiden Johnson-Körper J91 und J92 tragen auch
den Namen Rotunde.
Man überzeuge sich in 3D selbst, dass bei ihnen
zwei Kuppeln aufeinander liegen.
Bei J91 sind die Kuppeln identisch und um 180° gegeneinander
gedreht.
Es gibt keine ebene Grundfläche, die Deckflächen
sind in dieser Ansicht Dreiecke.
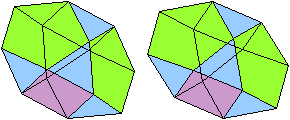
Vorderansicht Vorderansicht
|
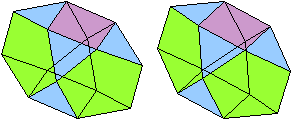
Rückansicht
Rückansicht
|
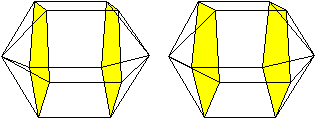
Bei J91 sind die Kuppeln verschieden. Es
gibt keine ebene Grundfläche, die Deckflächen sind in dieser
Ansicht ein Sechseck und ein Dreieck.
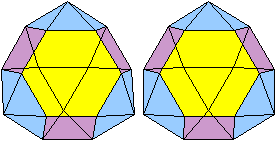
Vorderansicht Vorderansicht
|
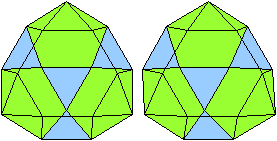
Rückansicht
Rückansicht
|
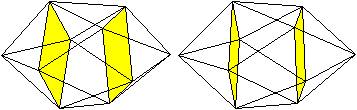
Hier sind beide Körper
noch einmal, dieses Mal blickt man in die Körper. Dazu vertauscht
man die Bildpaare.
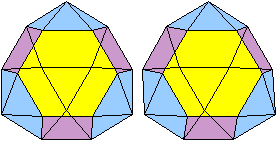
Blick ins Innere
Blick ins Innere
|
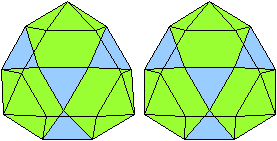
Blick ins Innere Blick ins Innere
|
Bipyramiden
top
Auf meiner Seite Bipyramiden
stelle ich sechs weitere Johnson-Körper vor.
J12 Dreiecksbipyramide
J13
Fünfecksbipyramide.
J14
Verlängerte triangulare Bipyramide
J15
Verlängerte tetragonale Bipyramide
J16
Verlängerte pentagonale Bipyramide
J17
Verdreht verlängerte Quadratbipyramide
Der Vollständigkeit
halber folgen noch die beiden Pyramiden unter den Johnson-Körpern.
J1 Quadratpyramide
J2 Fünfeckpyramide
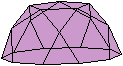
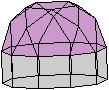
Kuppeln im Internet
top
Deutsch
Werner Brefeld
Geodätische
Kuppeln
Wikipedia
Johnson-Körper,
Geodätische
Kuppel, Kuppel
Englisch
Eric W.Weisstein
Johnson
Solid,
Triangular
Cupola, Square
Cupola, Pentagonal
Cupola, Pentagonal
Rotunda,
Geodesic
Dome
Poly
A program
for downloading (Poly is a shareware program for exploring and constructing
polyhedra)
Mit diesem Programm entstanden die meisten Bilder
dieser Seite.
Wikipedia
Johnson
solid,
Triangular
cupola,
Square
cupola,
Pentagonal
cupola,
Pentagonal
rotunda, Geodesic
dome, Dome
WolframAlpha
triangular
cupola, square
cupola, pentagonal
cupola, pentagonal
rotunda
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2010 Jürgen Köller
top |

 ...
...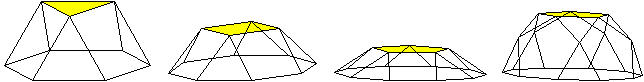
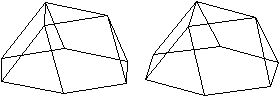
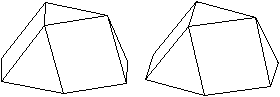
 ...
... ...
...
 ...
...
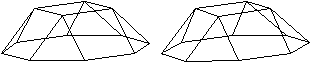
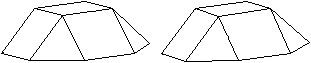
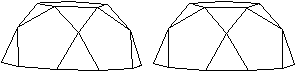
 ...
...