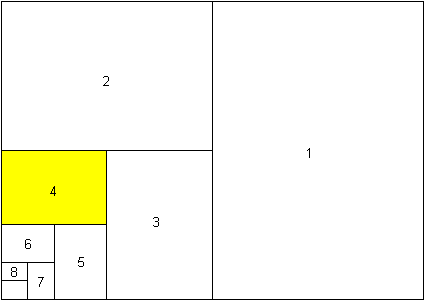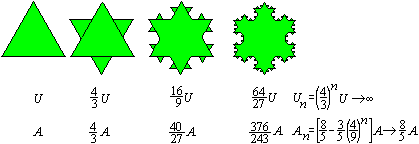|
Geometrische Folgen und Reihen
|
Was ist eine geometrische Folge?
Eine Folge heißt geometrisch, wenn der Quotient
zweier aufeinander folgender Glieder konstant ist.
Anders ausgedrückt:
Eine Folge heißt geometrisch, wenn jedes Glied
aus dem vorhergehenden durch Multiplikation mit einer Konstanten, dem Quotienten,
hervorgeht.
Formelsprache
Ist a das Anfangsglied und q der konstante Quotient,
so heißt die Folge a, aq, aq², aq³, ... aqn-1
oder
ai=aqi-1,
i = 1, 2, 3, ..., n.
Die Variablen a und q stehen für reelle Zahlen.
Damit man immer einen Quotienten bilden kann, dürfen
a und q nicht gleich Null sein.
Ist q=1, so sind alle Glieder gleich a. Dagegen ist nichts
einzuwenden. Es ist aber zweckmäßig, q=1 trotzdem nicht zuzulassen,
da unten in Formeln q-1 im Nenner steht.
Eine rekursive Darstellung der geometrischen Folge ist
a1=a und ai=qai-1 , i = 2, 3, ... n.
Name
Vielleicht ist der folgende Satz der Grund für den
Namen geometrische Folge.
Satz: Jedes Glied einer geometrischen Folge ist das geometrische
Mittel der beiden Nachbarglieder.
Herleitung
ai-1*ai+1=aqi-2 * aqi
=a2q2i-2 =(aqi-1)2=ai2
oder ai=sqrt(ai-1*ai+1), wzbw..
Zu ergänzen ist noch 1<i<n+1.
Zahlenbeispiele:
2
6
18
54
a=2, q=3
|
2
2/3
2/9
2/27
a=2, q=1/3
|
2
-6
18
-54
a=2, q=-3
|
2/3
-2/9
2/27
-2/81
a=2/3, q=-1/3
|
sqrt(2)
2
2sqrt(2)
4
a=sqrt(2),
q=sqrt(2)
|
sqrt(2)
sqrt(6)
3sqrt(2)
3sqrt(6)
a=sqrt(2), q=sqrt(3)
|
Ist q<1, so ist die Folge fallend. - Ist q>1, so ist die
Folge steigend. - Ist q<0, wechseln die Vorzeichen.
Graphische Darstellungen
top
Spiralen
...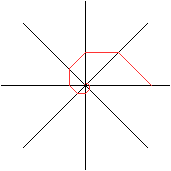 ... ... |
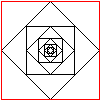
Die Glieder einer geometrischen Folge lassen sich als
eine Spirale aus Strecken graphisch darstellen.
In der Zeichnung ist q=(1/2)sqrt(2) |
Beweis
...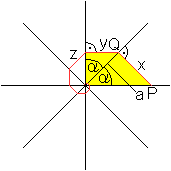 ... ... |
Gegeben seien n Geraden, die sich in einem Punkt schneiden.
Sie sollen so liegen, dass die Zwischenwinkel gleich sind. - Man fällt
von einem auf einer Geraden liegenden Punkt P aus das Lot auf die darüber
liegende Gerade, von da aus auf die nächste usw. . Es entsteht die
rote Spirale.
Das Augenmerk ist auf die beiden rechtwinkligen, gelben
Dreiecke gerichtet mit den gleichen Winkeln alpha=360°/n und der gemeinsamen
Seite a.
Es gilt tan(alpha)=x/a und sin(alpha)=y/a. Daraus folgt
y/x=sin(alpha)/tan(alpha)=cos(alpha).
Entsprechend gilt auch z/y=cos(alpha) usw. |
Ergebnis: Der Quotient der Längen aufeinanderfolgender
Strecken x, y, z, ... ist cos(alpha) und damit konstant. Sie bilden deshalb
eine geometrische Folge.
In der Zeichnung ist alpha
gleich 45°. Dann ist der konstante Quotient q=cos(45°)=(1/2)sqrt(2).
...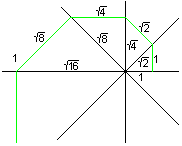 ... ... |
Man kann die Spirale auch so anlegen, dass sie immer
weiter wird.
Dann muss man q>1 wählen und auf den Geraden Senkrechte
errichten statt Lote fällen.
In der Zeichnung ist q=sqrt(2).
Wieder ist wie oben cos(alpha)
der konstante Quotient. |
Interessant ist der Grenzfall,
dass die Winkel zwischen den Geraden gegen Null gehen. Dann wird aus der
Spirale aus Geradenstücken eine logarithmische Spirale.
Zickzacklinie
... ... ... |
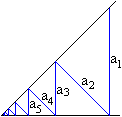 ... ... |
Die Glieder einer geometrischen Folge lassen sich auch
als (blaue) Zickzacklinie in einem Winkelraum grafisch darstellen.
Zur Erklärung betrachte man noch einmal die Figur
ganz links. Fällt man das Lot von Q aus zurück auf die Ausgangsgerade,
auf der P liegt, und fährt entsprechend fort, so entsteht die Zickzacklinie. |
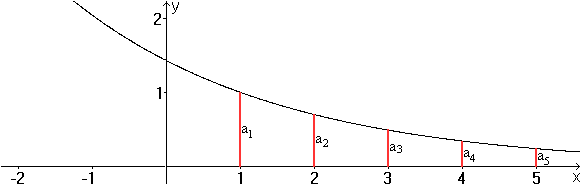
Graph
Der Graph der Exponentialfunktion
f(x)=0,7x-1 liefert an den Stellen x=1, 2, 3, 4, 5 die Glieder
der Folge.
Baumdarstellung
... ... ...
|
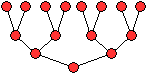
Das ist die Baumdarstellung der geometrischen Folge 1,
2, 4, 8, ... oder ai=1*2i-1, i=1,
2, 3, ... , n.
Sie heißt auch binärer Baum. |
Geometrische Reihe
top
Zu einer Folge gibt es als Erweiterung die Folge der
Partialsummen.
D.h., zur Folge an gibt es die Reihe sn
= a1 +a2 +a3 +...+an.
Für die geometrische
Folge ist es die Reihe sn = a + aq + aq² + aq³ + ...+
aqn-1.
Die Summe fasst man zusammen zu sn = a(1-qn)/(1-q).
Herleitung
sn = a +aq+ aq²+ aq³+ ...+aqn-1
qsn= aq+ aq²+ aq³+
...+aqn-1+aqn
Die linken und
rechten Terme subtrahiert man und erhält sn-qsn
=a-aqn oder sn =a(1-qn)/(1-q),
wzbw..
Ist q>1, schreibt man besser
sn = a(qn-1)/(q-1).
Unendliche
geometrische Folge und Reihe top
... ... ... |
Links wird die geometrische Folge mit q=(1/2)sqrt(2)
graphisch dargestellt. Man erkennt, dass die Glieder der Folge immer kleiner
werden und sich Null immer mehr nähern.
Das bestätigt auch die Formel an=aqn-1.
Die Potenz qn-1 und damit an gehen gegen Null.
Interessant ist das Verhalten der zugehörigen geometrischen
Reihe sn.
Die Länge der Zickzacklinie ist eine endliche Zahl. |
Nach der Formel sn = a(1-qn)/(1-q)
geht qn gegen Null und damit sn nach Grenzwertsätzen
gegen s=a/(1-q) für n gegen Unendlich und q<1.
Drei Zahlenbeispiele
(1) Ist q=(1/2)sqrt(2) wie in der Zeichnung, so
ist s=1/(1-q)=1/(1-[1/2sqrt(2)]=2/[2-sqrt(2)]=2+sqrt(2). Das ist rund 3,1.
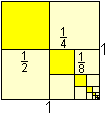
(2) 1 + 1/2 + 1/4 + 1/8 + 1/16 + ... = 2
(3) 1 - 1/2 + 1/4 - 1/8 + 1/16 - ... = 2/3
Exponentialfunktion
top
Eine Funktion mit f(x)=ax oder f(x)=ex*ln
a heißt Exponentialfunktion, wobei a>0 und a nicht gleich 1
ist.
Der größtmögliche Definitionsbereich
ist die Menge der reellen Zahlen, D=|R.
Ist die Menge der natürlichen Zahlen |N der Definitionsbereich,
so wird daraus die geometrische Folge an=qn
(n=1, 2, 3, ...).
Man kann also eine geometrische Folge auch als Funktion
über der Menge der natürlichen Zahlen auffassen.
Es folgen zwei Beispiele.
...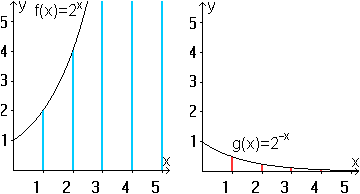 ... ... |
Zu f(x)=2x gehört die Folge 2, 4, 8,
16, 32, ...
Zu g(x)=2-x gehört die Folge 1/2, 1/4,
1/8, 1/16, 1/32, ...
Man kann an der Zeichnung die Monotonie der Folgen erkennen. |
Arithmetische
Folgen und Reihen top
Die arithmetischen Folgen und Reihen können wie
die geometrischen beschrieben werden. Man muss jedoch nicht von konstanten
Quotienten, sondern von konstanten Differenzen ausgehen. Das macht den
Sachverhalt einfacher.
Definition
Eine Folge heißt arithmetisch, wenn die Differenz
zweier aufeinander folgender Glieder konstant ist.
Anders ausgedrückt:
Eine Folge heißt arithmetisch, wenn jedes Glied
aus dem vorhergehenden durch Addition einer Konstanten, der Differenz,
hervorgeht.
Formelsprache
Ist a das Anfangsglied und d die konstante Differenz,
so ist die Folge a, a+d, a+2d, a+3d, ... , a+(n-1)d oder
ai=a+(i-1)d, i = 1,
2, 3, ..., n.
Die Variablen a und d stehen für reelle Zahlen.
Eine rekursive Darstellung der arithmetischen Folge ist
a1=a und ai=ai-1+d, i = 2, 3, ... n.
Name
Vielleicht ist der folgende Satz der Grund für den
Namen arithmetische Folge.
Satz: Jedes Glied einer arithmetischen Folge ist das
arithmetische Mittel der beiden Nachbarglieder.
Herleitung
ai-1+ ai+1 = [a+(n-2)d+a+nd) =
a+nd-2d+a+nd =2[a+(n-1)d]=2ai oder ai =(1/2)(ai-1+ai+1),
wzbw..
Zu ergänzen ist noch 1<i<n+1.
Zahlenbeispiele
1
2
3
4
...
a=1,
d=1
|
5
10
15
20
...
a=5,
d=5
|
2
5
8
11
...
a=2,
d=3
|
2
2 1/3
2 2/3
3
...
a=2,
d=1/3
|
2
-1
-4
-7
...
a=2,
d=-3
|
2/3
1/3
0
-1/3
...
a=2/3,
d=-1/3
|
Ist d>0, so ist die Folge steigend. - Ist d<0, so ist
die Folge fallend.
Graph
An die Stelle der Exponentialfunktion
tritt die lineare Funktion.
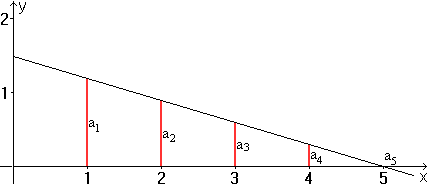 Die dargestellte Folge ist 1,2; 0,9; 0,6; 0,3;
0.
Die dargestellte Folge ist 1,2; 0,9; 0,6; 0,3;
0.
Arithmetische
Reihe
Zur arithmetrischen Folge gibt es die Reihe sn
= a + [ a+d] + [a+2d] + [a+3d] + ... + [a+(n-1)d].
Diese Summe fasst man zusammen zu sn = (1/2)n(a+an)
oder ausführlich zu sn = an+(1/2)d²n-(1/2)dn.
Herleitung
Man kann schreiben
sn = a1 + a2
+ a3 + ... + an-2 + an-1 + an
= a + [a+d] + [a+2d] + ... + [an -2d] + [an
-d] + an oder
sn = an + an-1
+ an-2 + ... + a3 + a2 + a1
= an + [an-d] + [an-2d] + ... + [a+2d]
+ [a+d] + a
Bildet man die Summe der untereinander stehenden Summanden
rechts, so ergibt sich n-mal die gleiche Summe a+an.
Es ist also 2sn =n(a+an)
oder sn =(1/2)n(a+an), wzbw.
Im Spezialfall
a=1 und an=n ergibt sich die Summe der natürlichen
Zahlen 1+2+3+...+n = (1/2)n(n+1).
Mehr über arithmetische
Folgen und Reihen findet man unten in der Linkliste und auf meiner Seite
Dreieckszahlen.
Es folgen Anwendungen der Formeln der geometrischen Folgen
und Reihen.
Weizen-Schachbrett-Aufgabe
top
Aufgabe
In einem Lehrbuch der Mathematik von 1940 (1) findet
man, wie in fast allen Lehrbüchern, die geometrische Folgen behandeln,
die berühmte Weizen-Schachbrett-Aufgabe.

Dahinter steckt eine Legende, die man auf der Wikipedia-Seite
Sissa
ibn Dahir (URL unten) nachlesen kann.
Lösung
Die Anzahl der Weizenkörner ist 1+2+22+
... +263 = a(qn-1)/(q-1) = (264-1)/(2-1)=
264-1= 18.446.744.073.709.551.615.
Gerundet sind das 1,84*1019 Körner.
Damit ist die Aufgabe gelöst.
Diese Riesenzahl nimmt erst Gestalt an, wenn man sie
veranschaulicht.
Veranschaulichung
2007 betrug die Weizenproduktion weltweit m=607.047.690
t oder gerundet m=610.000.000 t = 6,1*108 t.
(Quelle: http://de.wikipedia.org/wiki/Weizen)
Sind diese Weizenmenge m und die Weizenmenge auf den
Schachbrett M vergleichbar?
Angenommen, 20 Körner gehen auf 1g.
Dann ist die Masse M=(1,84*1019):(20*1.000.000)
t = 92.000.000.000 t = 9,2*1010 t.
Der Quotient M/m=(9,2*1010 t):(6,1*108
t)
= 1500 kann gedeutet werden als die 1500fache Weizenproduktion von 2007.
Rein-periodische
Dezimalbrüche top
Die rationalen Zahlen oder Bruchzahlen sind von der Form
a/b, wobei für a und b ganze Zahlen einzusetzen sind mit der Ausnahme
b=0. Man erhält eine gute Vorstellung von der Größe der
Zahlen, wenn man sie als Dezimalbrüche darstellt.
Beispiele sind 7/20=0,35,
4/33=0,121212... und 7 5/12=7,41666...
.
Diese Zahlen repräsentieren die drei möglichen
Darstellungen eines Dezimalbruches, die endliche, die rein-periodische
und die gemischt-periodische. Man kann sich überlegen, dass allein
der Nenner bestimmt, welche Klasse vorliegt.
Im ersten Fall ist der Nenner eine Zahl, die nur 2 und
5 als Teiler hat (20=2*2*5).
Im zweiten Falle hat der Nenner weder 2 noch 5 (33=3*11)
als Teiler.
Im dritten Fall hat der Nenner mindestens eine 2 oder
5, aber auch mindestens einen von 2 und 5 verschiedenen Teiler (12=2*2*3).
An drei weiteren Beispielen
wird gezeigt, dass rein-periodische Dezimalzahlen geometrische Reihen sind.
>0,444... = 4*10-1+4*10-2+4*10-3+...
.
Es gilt a=4*10-1 und q=10-1. -
Der Grenzwert ist s=a/(1-q)=(4/10)/(9/10)=4/9.
>0,121212... = 12*10-2+12*10-4+12*10-6+...
Es gilt a=12*10-2 und q=10-2. Der
Grenzwert ist s=a/(1-q)=(12/100)(99/100)=4/33.
>0,0369369369...=369/10-4+369/10-7+369/10-10+....
Es gilt a=369/10-4 und q=10-3.
Der Grenzwert ist s=a/(1-q)=(369/10000)(999/1000)=22/555.
Auch gemischt-periodische Zahlen können als geometrische
Reihen angesehen werden, wenn man den nichtperiodischen Anteil als Summand
vorwegnimmt.
Zinseszinsen
top
Aufgabe
Ein Kapital von K0=100 € wird auf n=100
Jahre angelegt. Die Zinsen betragen p%=3%.
Auf welchen Betrag wird das Kapital anwachsen?
Lösung
Im 1.Jahr wächst K an auf K1=K0+(p/100)K0=K0(1+p/100)=K0q.
Im 2.Jahr wächst K an auf K2=K0q+(p/100)K0q=K0q(1+p/100)=K0q2.
Im 3.Jahr wächst K an auf K3=K0q2+(p/100)K0q2=K0q2(1+p/100)=K0q3.
...
Im n.ten Jahr beträgt das Endkapital Kn=K0qn.
Das ist die Formel einer geometrischen Folge.
Ist K0=100 €,
n=100 und p=3,
so ist q=1,03 und das Kapital nebst Zinsen und Zinseszinsen
K100
= 100 €*1,03100 = 1921,86 €.
Werden die Zinsen am Ende
eines jeden Jahres abgehoben, so ist K100' = K0+100*(3/100)K0
=
100 €+300 € = 400 €.
Währungsreformen z.B.
machen die Rechnungen unrealistisch, aber die Aufgabe veranschaulicht gut
den exponentiellen Anstieg einer geometrischen Folge.
Hier ist noch ein Beispiel
aus dem Leben.
Ich zeige mein altes Postsparbuch, heute auch ein Zeitdokument
zum Lastenausgleich.

1.Blatt
|

6.Blatt
Die Namen der Postbeamten habe ich unlesbar gemacht.
|
Überschlagsrechnung
dazu: K14 = 11 DM*1,0414 = 19 DM
Achilles
und die Schildkröte top
Aufgabe
Achilles verfolgt eine Schildkröte, die einen Vorsprung
von 100 Fuß hat, mit 10mal so großer Geschwindigkeit. Wo holt
Achilles die Schildkröte ein?
Lösung
Wenn Achilles 100 Fuß zurückgelegt hat, ist
die Schildkröte 10 Fuß weitergekrochen.
Wenn Achilles diese 10 Fuß zurückgelegt hat,
ist die Schildkröte 1 Fuß weitergekrochen.
Wenn Achilles 1 Fuß zurückgelegt hat, ist
die Schildkröte 0,1 Fuß weitergekrochen.
Wenn Achilles 0,1 Fuß zurückgelegt hat, ist
die Schildkröte 0,01 Fuß weitergekrochen.
...
Überholt wird die Schildkröte schließlich
bei 111,111... Fuß = 111 1/9 Fuß.
Das Problem ist als Paradoxon
des Zenon bekannt und gilt als eine Spitzfindigkeit, wie sie bei den Sophisten
beliebt war.
Heute ist das Problem in
der Mathematik nichts Besonderes, seit man den Grenzwert eingeführt
und akzeptiert hat.
Eine Summe mit unendlich vielen Summanden wie 0,111...=1/10+1/100+1/1000+
... muss nicht unendlich groß werden.
Der Grenzwert ist die Summe.
Potenzierung
in der Homöopathie top
Eine "Urtinktur" ist in der Homöopathie meist nicht
direkt eine Medizin, sondern sie wird erst zu einer Medizin mit Verdünnungsmitteln
wie Alkohol, destilliertem Wasser oder Ähnlichem.
Dabei geht man so vor, dass man in einem ersten Schritt
im Verhältnis 1:10 verdünnt.
Dann nimmt man davon eine Probe und verdünnt diese
wieder im Verhältnis 1:10, also im ganzen 1:100.
Eine Probe davon, wieder im Verhältnis 1:10 verdünnt,
führt zur Verdünnung 1:1000, bezogen auf die Urtinktur.
Die drei bisher genannten Verdünnungen tragen die
Kennzeichnungen D1, D2 und D3 auf der so hergestellten Medizin.
Mit dem Verdünnen ist ein Schütteln verbunden,
das zusammen nennt man Potenzieren im Sinne von Verstärkung.
Eine Verstärkung wie D8 gibt es durchaus.
D8 entspricht einer Verdünnung von 1:100.000.000.
D.h., 1cm³ Wirkstoff kommt auf 100.000.000 cm³=100.000
Liter=1.000hl=100m³= 4m*5m*5m.
Das letzte Produkt kann man als Volumen eines Quaders
mit der Länge 5m, der Breite 5m und der Höhe 4m auffassen.
Ein Würfel von 1cm³ ist winzig in diesem riesigen
Raum. - Kein Kommentar.
Zusammenfassung: Zu D1, D2,
... gehört die geometrische Folge an=10-n.
Chromatische Tonleiter
top
Es besteht ein Zusammenhang zwischen der geometrischen
Folge und den Tönen des Klaviers.
Dort treten nämlich Schwierigkeiten auf, wenn man
z.B. von der Tonart C-Dur zu D-Dur wechselt.
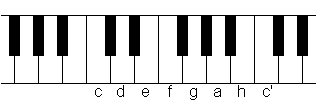
C-Dur-Tonleiter
|
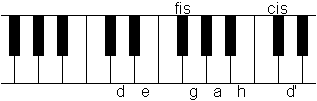
D-Dur-Tonleiter
|
Die Höhe eines Tones
wird durch die Frequenz bestimmt.
Bei einer Tonleiter stehen sie in bestimmten, einfachen
Beziehungen zueinander.
Die folgende Tabelle zeigt in der zweiten Zeile die Verhältnisse
der Frequenzen der Töne zum Grundton c.
In der dritten und vierten Zeile stehen die sich daraus
ergebenden Verhältnisse der Frequenzen nebeneinander liegender Töne.
Bezeichnungen
Frequenzverhältnisse
Intervalle
Intervalle |
c
1:1
.
.
|
.
.
9:8
=1,12
|
d
9:8
.
.
|
.
.
10:9
=1,11
|
e
5:4
.
.
|
.
.
16:15
=1,07
|
f
4:3
.
.
|
.
.
9:8
=1,12
|
g
3:2
.
.
|
.
.
10:9
=1,11
|
a
5:3
.
.
|
.
.
9:8
=1,12
|
h
15:8
.
.
|
.
.
16:15
=1,07
|
c'
2:1
.
.
|
Dieses sind die Merkmale der sogenannten diatonischen
Tonleiter.
Gibt man eine solche Tonleiter
in C-Dur vor, so entstehen Konflikte, wenn man auf die Tonart D-Dur übergehen
will.
Bei einer diatonischen C-Dur-Tonleiter wird das Intervall
der Töne d/e nach der Tabelle durch das Verhältnis 10:9=1,111
bestimmt.
Lässt man die Tonleiter in d beginnen, gehört
zur gleichen Abfolge der Töne d/e das Verhältnis 9:8=1,125.
Das ist ein Widerspruch.
Der Widerspruch wird gelöst
durch einen Kompromiss.
Die diatonische Tonleiter wird in Maßen aufgegeben
und durch die sogenannte chromatische Tonleiter ersetzt.
Von der diatonischen Tonleiter übernimmt man die
Eigenschaft, dass die Frequenz des Grundtons (hier c) und des nächsten
Obertons (c') im Verhältnis 1:2 stehen. Neu ist, dass man die Frequenzen
der Töne c cis d dis e f fis g gis a b h c' zu einer geometrischen
Folge anordnet.
Das seien die Frequenzen als geometrische Folge: a, aq,
aq2, aq3, aq4, aq5, aq6,
aq7, aq8, aq9, aq10, 2a=aq21.
Aus 2a=aq12 folgt q12.=2 oder q=21/12
=1,06.
Dieser Quotient ist das neue Verhältnis der Frequenzen
aufeinanderfolgender Töne.
Die Frequenzverhältnisse einer Tonleiter sind nur
leicht abgeändert, wie die folgende Tabelle zeigt.
Bezeichnungen
Frequenzverhältnisse
...
Frequenzverhältnisse
... |
c
1:1
=1,000
q0
=1,000 |
d
9:8
=1,125
q2
=1,123 |
e
5:4
=1,250
q4
=1,260 |
f
4:3
=1,333
q5
=1,336 |
g
3:2
=1,500
q7
=1,498 |
a
5:3
=1,667
q9
=1,682 |
h
15:8
=1,875
q11
=1,888 |
c'
2:1
=2,000
q12
=2,000 |
Die abgeänderten Frequenzen stehen in roter Schrift.
Man kann nachlesen, dass nur geschulte Musiker den Unterschied
heraushören.
Quelle (3) Seite 33ff.
Papier falten
top
Aufgabe
Ein Blatt Schreibmaschinenpapier von 80g/m² hat
eine Dicke von ca. 0,1mm.
Wie dick wird der Papierstapel, wenn man das Blatt siebenmal
jeweils in der Mitte faltet?
Lösung
Anzahl der Faltungen
Dicke
... |
1x
2*0,1mm
=0,2mm |
2x
22*0,1mm
=0,4mm |
3x
23*0,1mm
=0,8mm |
... |
7x
27*0,1mm
=12,8mm |
... ... ... |
... ... ... |
Faltet man tatsächlich ein Din A 4-Blatt mehrmals,
kommt man bei bestem Willen nicht über fünffaches Falten hinaus.
Ist das Blatt größer und dünner, könnte
man noch weiter falten. Es gibt aber wegen des exponentiellen Anstiegs
auf jeden Fall eine Grenze.
Es hieß, mehr als 7x kann ein Blatt Papier nicht
gefaltet werden. |
Diese Anzahl Sieben wurde im Januar 2002 von der High-School-Schülerin
Britney Gallivan korrigiert, die erfolgreich ein großes Blatt Papier
12x in der Technik "Single Direction Folding" unter Geräteeinsatz
faltete und auch dafür eine Formel entwickelte.
Mehr findet man z.B. auf der Seite Folding bei
Mathworld (URL unten).
Auch an anderen Stellen meiner Homepage kommen geometrische
Folgen und Reihen vor.
Kochkurve und
Sierpinski-Dreieck
Geometrische
Folgen und Reihen im Internet top
Deutsch
Wikipedia
Geometrische
Folge, Geometrische
Reihe, Geometrisches
Mittel, Arithmetische
Folge, Sissa
ibn Dahir
Achilles
und die Schildkröte, Zinseszins,
Gleichstufige
Stimmung, Binärbaum,
Ahnentafel
Englisch
Eric W. Weisstein (MathWorld)
Geometric
Sequence, Geometric
Series, Zeno's
Paradoxes, Folding
Wikipedia
Geometric
progression, Geometric
mean, Arithmetic
progression, Wheat
and chessboard problem, Paper
folding, Compound
interest, Equal
temperament, Binary
tree, Ahnentafel
Referenzen top
(1) Otto Zoll: Mathematisches Lehr- und Arbeitsbuch,
Braunschweig 1940
(2) Lambacher/Schweizer: Analysis, Stuttgart 1954
(3) Jean Pütz (Hrsg.): Hifi, Ultraschall und Lärm,
Köln 1973
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2009 Jürgen Köller
top |

 ...
... ...
... ...
... ...
...
 ...
... ...
...



 ...
... ...
...