|
Was ist eine Spirale?
Eine Spirale ist eine ebene oder räumliche Kurve,
die in bestimmter Weise um eine Mitte läuft.
Es folgen unterschiedliche
Spiralen, die meisten werden durch Formeln erzeugt.
Spiralen
durch Polargleichungen
top
Archimedische Spirale
top
Die Spirale kann man durch eine Überlagerung zweier
Bewegungen eines Punktes erzeugen, nämlich durch eine gleichförmige
Bewegung längs eines Strahls vom Anfangspunkt aus und durch eine gleichförmige
Kreisbewegung des Strahls um den Anfangspunkt herum.
.......................... . |
|
|
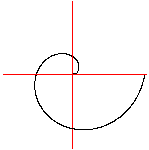
(1) Die gleichförmige Bewegung links bewegt einen
Punkt nach rechts. - Das Bild enthält neun Momentaufnahmen.
(2) Die gleichzeitig stattfindende gleichförmige
Kreisbewegung in der Mitte bringt die Punkte auf eine Spiralbahn.- Nach
jeder Achteldrehung wird ein Punkt gesetzt.
(3) Die Spirale entsteht als Kurve, wenn der Ort zu jedem
Zeitpunkt festgehalten wird.
Man gelangt in Analogie zum
Kreis zu Formeln.
Kreis
... ... |
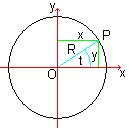Es sei P ein beliebiger Punkt eines Kreises mit dem Radius
R, der in der Mittelpunktslage gegeben ist.
Es gibt u.a. drei Darstellungen des Kreises.
(1) Koordinatengleichung: x²+y² = R² oder
[y = sqr(R²-x²) und y = -sqr(R²-x²)],
(2) Parametergleichungen: x(t) = R cos(t), y(t) = R sin(t),
(3) Polargleichung: r(t) = R. |
In der (einfachen) Polargleichung (3) wird ein Punkt durch
das Paar (Radius OP, Winkel t) angegeben. Der Radius ist die Entfernung
des Punktes vom Nullpunkt (0|0). Der Winkel liegt zwischen dem Radius und
der positiven x-Achse, sein Scheitel im Nullpunkt.
Spirale
Bei der einfachsten Spirale, der Archimedischen Spirale,
sind Radius r(t) und Winkel t proportional. So bietet sich die folgende
Polargleichung an:
(3) Polargleichung: r(t) = at [a ist eine Konstante].
Daraus folgt
(2) Parametergleichungen x(t) = at cos(t), y(t) = at
sin(t),
(1) Koordinatengleichung: x²+y² = a²[arc
tan (y/x)]².
... ...
|
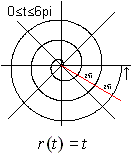
Die Archimedische Spirale links beginnt im Nullpunkt
und beschreibt um ihn eine immer weiter werdende Kurve mit drei Umläufen.
Der Abstand der Spiral-Äste bleibt gleich.
Genauer: Die Entfernungen benachbarter Kurvenpunkte auf
einer Nullpunktsgeraden sind konstant. |
... ... |
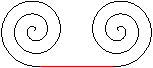Spiegelt man eine Archimedische Spirale, so erhält
man eine neue Spirale mit dem entgegegesetzten Richtungssinn.
Beide Spiralen laufen von innen nach außen. Schaut
man auf die Spiralen, so beschreibt die linke eine Linkskurve, die rechte
eine Rechtskurve. |
Verbindet man die beiden Spiralen durch eine gerade oder
gekrümmte Linie (rot), so entsteht die Doppelspirale.
Logarithmische
Spirale (Spirale des Bernoulli, englisch: Equiangular Spiral) top
... ...
|
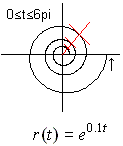
(1) Die Polargleichung lautet r(t)
= exp(t).
(2) Die Parametergleichung ist
x(t)
= exp(t) cos(t), y(t) = exp(t) sin(t).
(3) Die Koordinatengleichung ist
y = x tan[ln(sqr(x²+y²))].
Auch die logarithmische Spirale
läuft von innen nach außen.
Die Spirale hat eine charakteristische
Eigenschaft: Jede Nullpunktsgerade (rot) schneidet die Spirale unter demselben
Winkel. |
Weitere Spiralen top
Ersetzt man in der Polargleichung
zur Archimedischen Spirale den Term r(t)=at durch andere Funktionsterme,
so erhält man eine Folge neuer Spiralen. Es folgen sechs Spiralen,
die mit den Grundfunktionen mit f(x)=x^a [a=2,1/2,-1/2,-1] und f(x)=exp(x),
f(x)=ln(x) gebildet worden sind. Dabei unterscheidet man zwei Gruppen,
wenn man den Parameter t von 0 aus wachsen lässt.
... ......... |
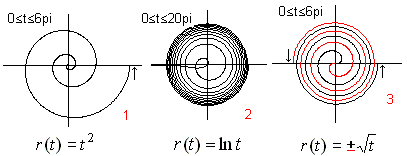Ist der Betrag einer Funktion r(t) monoton steigend,
so verlaufen die Spiralen von innen nach außen. Im allgemeinen beginnen
sie im Nullpunkt und gehen über alle Grenzen.
Die Spirale 1
heißt parabolische Spirale oder Spirale von Fermat. |
... .... |
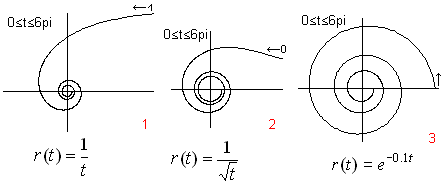Ist der Betrag einer Funktion r(t) monoton fallend, so
verlaufen die Spiralen von außen nach innen. Im allgemeinen laufen
sie auf ein Zentrum zu, das sie nie erreichen. Dann liegt ein Pol vor.
Die Spirale 2
heißt hyperbolische Spirale oder Lituus (Krummstab). |
Für die verschiedenen Spiralformeln wird jeweils ein
Vertreter mit einer für den Plotter geeigneten Gleichung ausgewählt.
Clothoide (Cornu-Spirale)top
... .... |
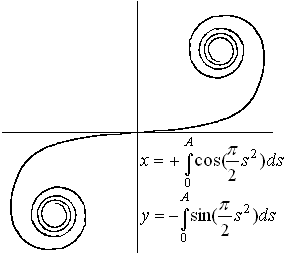Die Clothoide ist eine Doppelspirale, deren Krümmung
mit der Entfernung vom Nullpunkt immer größer wird. Der Krümmungsradius
ist umgekehrt proportional zu ihrer Bogenlänge, gemessen vom Nullpunkt
aus.
Zwei Gleichungen mit den Fresnelschen Integralen, die
nur näherungsweise lösbar sind, bilden die Parameterdarstellung.
Eine wichtige Anwendung der Cornu-Spirale ist die Fresnelsche
Beugung am Spalt oder an einer Kante. Mit Hilfe der Cornu-Spirale kann
man Aussagen zur Lichtverteilung machen.
|
Georg Schön teilte mir
mit, dass er viel wichtiger findet, dass die meisten Kurven von Straßen
Klothoiden sind. Die Klothoide ist nämlich die Kurve, die ein Auto
zurücklegt, wenn man bei konstanter Geschwindigkeit das Lenkrad mit
konstanter Winkelgeschwindigkeit dreht.
Spiralen aus
Kreisbögen
top
Halbkreisspirale
... ... |
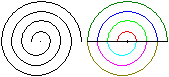Man kann stufenweise größer werdende Halbkreise
zu einer Spirale zusammensetzen.
Die Radien haben das Verhältnis 1 : 1.5 :
2 : 2.5 : 3..... |
Fibonacci-Spirale
... ... |
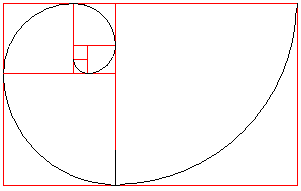Man zeichnet zuerst zwei kleine Quadrate übereinander.
Dann fügt man in Folge immer größer werdende Quadrate entgegengesetzt
dem Uhrzeigersinn hinzu.
In die Quadrate werden (schwarze) Viertelkreise eingezeichnet.
Sie bilden die Fibonacci-Spirale. |
Der Name der Spirale rührt von den Fibonaccizahlen her.
Schreibt man die Seitenlängen der Quadrate der Reihe nach auf, so
erhält man die Folge 1,1,2,3,5,8,13,21, ... Das sind die Fibonacci-Zahlen,
die sich nach der Rekursionsformel a(n)=a(n-1)+a(n-2) errechnen [a(1)=1,
a(2)=1, n>2].
Spiralen aus Strecken
top
... ... |
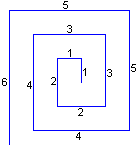Die Spirale besteht aus Strecken der Längen 1,1,2,2,3,3,4,4,....
Aufeinanderstoßende Strecken stehen paarweise aufeinander
senkrecht. |
... ... |
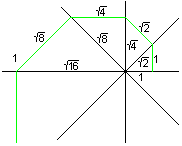Die Spirale wird in eine Geradenkreuzung
eingezeichnet, die aus vier Geraden besteht, die jeweils einen Winkel von
45° bilden. Man beginnt mit der horizontal liegenden Strecke 1 und
knickt die nächste Strecke so ab, dass sie auf der nächsten
Halbgeraden senkrecht steht. Die Strecken bilden eine geometrische Folge
mit dem konstanten Quotienten sqr(2).
Zeichnet man eine Spirale in ein
Geradenbüschel aus beliebig vielen Geraden, die gleiche Winkel einschließen,
so nähert sich die Streckenspirale einer logarithmischen Spirale,
wenn man die Winkel immer kleiner werden lässt. |
... ... |
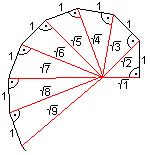Die nächste Spirale entsteht aus einer Kette von
rechtwinkligen Dreiecken, die jeweils eine Seite gemeinsam haben. Aus der
Hypotenuse eines Dreiecks wird eine Kathete des nächsten Dreiecks.
Erstes Glied ist das gleichschenklig-rechtwinklige Dreieck 1-1-sqr(2).
Die freien Katheten der Länge 1 bilden die Spirale.
Das Besondere ist, dass sich die Dreiecke in Seiten berühren,
deren Länge die Wurzeln aus den natürlichen Zahlen sind. Das
beweist man mit dem Satz des Pythagoras.
Diese Figur heißt Wurzelspirale oder Wurzelschnecke. |
... ... |
Ein Quadrat wird um seinen Mittelpunkt um jeweils 10°
gedreht und gleichzeitig so gestaucht, dass die Eckpunkte auf den Seiten
des vorhergehenden Quadrats liegen.
Ergebnis: Alle Eckpunkte beschreiben vier Spiralarme.
Je kleiner der Drehwinkel ist, desto mehr nähern sich die Spiralen
einer logarithmischen Spirale.
Man kann auch andere regelmäßige Vielecke,
z.B. ein gleichseitiges Dreieck, drehen und erhält ähnliche Figuren. |
Diese Grafiken erinnern an die Programmiersprache LOGO aus
den Kindertagen der Computerei (C64-Nostalgie).
Dreidimensionale
Spiralen
top
Helix
... ... |
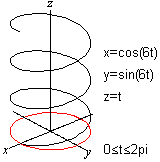Zeichnet man in der x-y-Ebene eine Kreislinie mit x=cos(t)
und y=sin(t) und zieht sie gleichmäßig in z-Richtung auseinander,
so ensteht eine räumliche Spirale.
Sie heißt zylindrische Spirale oder Helix. |
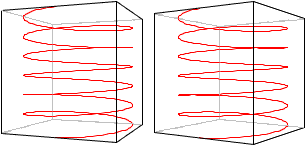
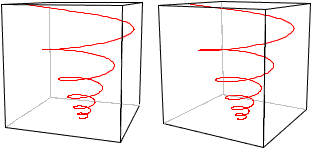
Das Bildpaar ermöglicht
eine dreidimensionale Sicht.
... ... |
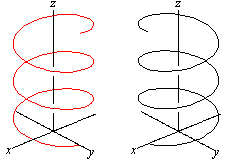Die Raumspirale wird an einer Vertikalebene gespiegelt.
Es entsteht eine neue Spirale (rot) mit dem entgegengesetzten Richtungssinn.
Umfasst man die rechte Spirale mit der rechten Hand und
zeigt der Daumen in z-Richtung, so geht es entgegen dem Uhrzeigersinn aufwärts.
Die Spirale hat eine Rechtsdrehung.
Für die linke Spirale muss man die linke Hand nehmen.
Die linke Spirale hat eine Linksdrehung.
Beispiel: Fast alle Schrauben haben eine Rechtsdrehung.
Sie sind rechtsgängig, passend für Rechtshänder. |
... ... |
In der "technischen" Literatur wird die Rechtsdrehung
so erklärt: Man wickelt ein rechtwinkliges Dreieck um einen Zylinder.
Es entsteht eine rechtsdrehende Spirale, wenn das Dreieck nach rechts steigt. |
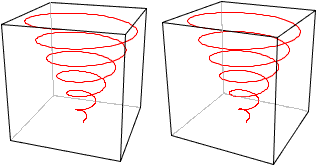
Konische
Spiralen
Kegelförmige Raumspiralen erhält man aus der
Archimedischen oder aus der logarithmischen Spirale. Sie heißen auch
konische Spiralen.
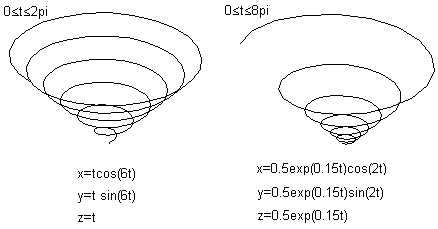
Die Bildpaare ermöglichen
eine dreidimensionale Sicht.
Loxodrome,
Sphärische Spirale
... ... |
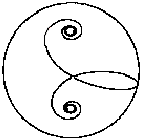Die Loxodrome ist eine Kurve auf einer Kugeloberfläche,
die die Meridiane unter gleichen Winkeln schneidet. Sie erscheinen auf
der Mercatorkarte als gerade Linien.
Die allgemeine Gleichung lautet:
x=cos(t) cos [tan-1(at)]
y=sin(t) cos[tan-1(at)]
z= -sin [tan-1(at)]
(a ist eine Konstante)
Man kann nachrechnen, dass x²+y²+z²=1
gilt. Diese Gleichung besagt, dass die Loxodrome auf der Kugeloberfläche
liegt. |
Allgemeiner gibt es zu jedem Rotationskörper eine Loxodrome.
Apfelmännchen-Spiralen
top
Die Koordinaten gehören zur Mitte der Bilder.
Schöne Spiralen findet man auch als Juliamengen. Hier
ein Beispiel:
Mehr über diese Graphiken findet man auf meiner Seite
Apfelmännchen.
Basteln von Spiralen
top
... ... |
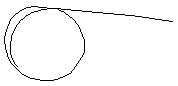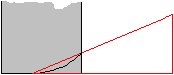
Zieht man zwischen dem Daumen und der Schneide eines
Messers unter Druck einen Papierstreifen, so krümmt sich dieser zu
einer Spirale. Er wird zu einer Locke, wenn man die Schwerkraft wirken
lässt.
Dieser Effekt wird auf Kunststoffbänder angewandt,
um die Enden eines Geschenkbandes ansehnlicher zu machen. |
Ich nehme an, dass dieser Effekt wie beim Bimetallstreifen
zu erklären ist.
Beim Bimetallstreifen werden zwei Streifen aus verschiedenen
Metallen aufeinandergeklebt. Erhitzt man den Bimetallstreifen, so dehnt
sich ein Metallstreifen stärker aus, der Bimetallstreifen krümmt
sich.
Beim Papierstreifen mag weniger der Temperaturunterschied
zwischen Ober- und Unterseite die Ursache sein. Mit dem Messer wird auf
einer Seite die Oberflächenstruktur verändert. Diese Seite wird
"kürzer".
Übrigens krümmt sich ein Papierstreifen auch
leicht, wenn man ihn hoch über eine Kerze hält.
... ... |
Die Bildung von Locken erinnert an ein Kinderspiel: Der
untere Teil des Stängels einer Butterblume (Löwenzahn) wird von
unten in Streifen längs des Stängels geschnitten, der oberer
Teil und die Blüte bleiben unangetastet. Taucht man die Blume ins
Wasser und lässt die Blüte auf der Wasseroberfläche schwimmen,
so bilden die Stängelstreifen nach einiger Zeit Locken. (Vorsicht,
Flecken.)
Zur Erklärung: Es dürfte die unterschiedliche
Wasseraufnahme der beiden Oberflächen eines Streifens eine Rolle spielen. |
Spiralen aus Metall
top
Spiralfiguren findet man als Verzierungen bei eisernen
Fenstergittern, Zäunen, Toren oder Türen. Man sieht sie überall,
wenn man darauf achtet.
... ... |
Ich fand schöne Spiralen in New Ulm, Minnesota,
USA.
Deutschamerikaner errichteten gegen 1900 als Symbol der
Freiheit eine Kopie des Hermannsdenkmals bei Detmold. Eiserne Gitter mit
vielen Spiralen schmücken den Aufgang (Foto).
Mehr über den amerikanischen und deutschen Hermann
findet man auf Wikipedia-Seiten (URL unten).
|
Auch Modeschmuck nimmt die
Spirale als Motiv.
... ... |
Annettes Schmuckspirale
 |
Spiralen,
Spiralen, Spiralen
top
Ammoniten, Anordnung der Sonnenblumenkerne, @, Bimetall-Thermometer,
Bischofsstab, Bretagne-Zeichen, Darm einer Kaulquappe, Diskus von Festós,
Doppelhelix der DNA, Doppelspirale, Doppelwendel der Glühbirne, Elektronenstrahl
im magnetischen Längsfeld, Exner-Spirale, Fadenpendels mit Reibung,
Fingerabdruck, Gehörn von Wildschafen, Gewinde, Schneckenminarett
in Samarra (Irak), Heizdraht in einer Kochplatte, Hoch- oder Tiefdruckgebiete,
Hühnerring, Korkenzieher, Kräuterspirale, Kreise eines Seeadlers,
Lakritzenschnecke, Lebensspirale, Locke, Lohn-Preis-Spirale, Lorenz-Attraktor,
Kopf des Musikinstruments Violine, Musikinstrument Horn, Pendelkörper
des sich überschlagenden Galilei-Pendels, Ranke, Rauchwirbel, rechtsdrehende
Milchsäure, Reliefband der Trajanssäule in Rom oder der Bernwardsäule
in Hildesheim, Rille einer Schallplatte, Rolle (Draht, Faden, Kabel, Schlauch,
Maßband, Papier, Verband), Mohnschnecke, Saugrüssel (Unterkiefer)
des Kohlweißlings, Schlange in Ruhestellung, Schlange des Äskulapstabes,
Schlingpflanzen, Schnecke des Innenohrs, Schneckenhaus, Schnörkel,
Schwanz des Seepferdchens, Schraube, Schraubenalge, Schraubenfeder, Segelflugzeug
aufsteigend, Spinnennetz, Spiralheftung, Spiralnebel, Spirallala, Spirelli-Nudeln,
Spirillen (z.B. Cholerabazillus), Sprungfedern einer Matratze, Spule, Spuren
auf einer CD oder DVD, Stoßzähne des Mammuts, Straße
eines Kegelberges, Tannenzapfen, Teilchenbahn im Zyklotron, Uhrfeder und
Unruh mechanischer Uhren, Violinschlüssel, Volute, Wärmespirale,
Wasserspirale des Archimedes, Wasserstrudel, Wendeltreppe (z.B. zwei Wendeltreppen
in der Glaskuppel des Reichstagsgebäudes in Berlin), Wirbelsturm,
Wissensspirale, Viren, Zapfen von Nadelgewächsen, Zunge und Wickelschwanz
des Chamäleons, Zyklone.
Spiralen im Internet
top
Deutsch
Asti
BEWEGUNGSFUNKTIONEN
Spiralen
Jürgen Berkemeier
Fibonacci-Spiralen
Matheprisma
Bewegungsfunktionen
(Spiralen 1 ) - (Spiralen online zeichnen)
Michael Komma
Fresnel-Beugung
am Einzelspalt (Cornu-Spirale)
Susanne Helbig, Kareen Henkel und Jan Kriener
Spiralen
in Naturwissenschaft, Technik und Kunst
Stephan Jaeckel und Sergej Amboni
Spiralen
in Natur, Technik und Kunst
(Referenz: Heitzer J, Spiralen, ein Kapitel phänomenaler
Mathematik, Leipzig 1998)
Wikipedia
Spirale,
Klothoide,
Logarithmische
Spirale, Fibonacci
Folge, Loxodrome,
Ulam-Spirale
Hermannsdenkmal,
Hermann
Heights Monument
Englisch
Ayhan Kursat ERBAS
Equiangular
Spiral
Bob Allanson
This
is a logarithmic spiral
David Eppstein (Geometry Junkyard)
Spirals,
(Links)
Eric W. Weisstein (MathWorld)
Spirals:
Archimedean
Spiral, Circle
Involute, Conical
Spiral, Cornu
Spiral, Curlicue
Fractal, Fermat's
Spiral, Helix,
Hyperbolic
Spiral, Logarithmic
Spiral, Mice
Problem, Nielsen's
Spiral, Polygonal
Spiral, Prime
Spiral, Rational
Spiral, Seashell,
Spherical
Spiral
Hop David (Hop's Gallery)
Riemann
sphere,
Ram's
Horn,
Spiral
Tile
Jan Wassenaar
spiral
John Macnab
Sculptures
Keith Devlin
The
Double Helix
Mark Newbold
Counter-Rotating
Spirals Illusion
Richard Parris (Freeware-Programme)
winplot
Xah Lee
Equiangular
Spiral, Archimedean
Spiral, Lituus,
Cornu
Spiral
Wikipedia
Spiral,
Archimedean
spiral,
Cornu spiral,
Fermat's
spiral,
Hyperbolic
spiral,
Lituus,
Logarithmic
spiral,
Fibonacci
spiral,
Golden
spiral,
Rhumb line,
Ulam
spiral,
Hermann
Heights Monument,
Hermannsdenkmal
Französisch
Robert FERRÉOL (COURBES
2D )
SPIRALE
COURBES
3D (SPHÉRO-CYLINDRIQUE, SPIRALE CONIQUE DE PAPPUS, SPIRALE CONIQUE
DE PIRONDINI, SPIRALE SPHÉRIQUE)
Referenzen top
(1) Martin Gardener: Unsere gespiegelte Welt, Ullstein,
Berlin, 1982 [ISBN 3-550-07709-2]
(2) Rainer und Patrick Gaitzsch: Computer-Lösungen
für Schule und Studium, Band 2, Landsberg am Lech, 1985
(3) Jan Gullberg: Mathematics - From the Birth of Numbers,
New York / London (1997) [ISBN 0-393-04002-X]
(4) Khristo N. Boyadzhiev: Spirals and Conchospirals
in the Flight of Insects, The College Mathematics Journal,
Vol.30, No.1 (Jan.,1999)
pp.23-31
(5) Jill Purce: the mystic spiral - Journey of the Soul,
Thames and Hudson, 1972, reprinted 1992
Ich bedanke mich bei Torsten Sillke für etliche
Tipps.
Feedback: Emailadresse auf meiner Hauptseite
Diese
Seite ist auch in Englisch vorhanden.
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2002 Jürgen Köller
top |
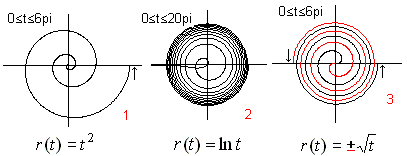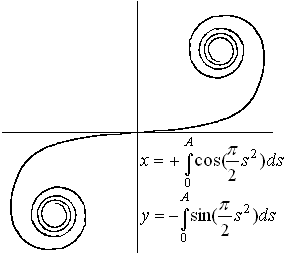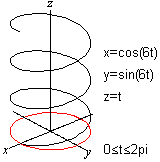
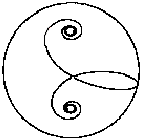