|
What is a Cuboctahedron?
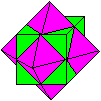
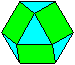
A cuboctahedron is a figure, which is formed by six squares and eight
equilateral triangles.
Two views follow:
A square and a triangle are lying parallel to the drawing plane.
Therefore these figures are true to the original.
Obviously the name cuboctahedron is formed
by the words cube and octahedron.
... ...
|
If you set squared pyramids on the faces of the cube, you can imagine
that a (green) cube and a (red) octahedron penetrate each other.
The intersection is the cuboctahedron. |
The cuboctahedron belongs to the 13 Archimedean
solids. I made a page (in German only).
Those who know how to use the 3D-View,
can see the cuboctahedron threedimensionally.
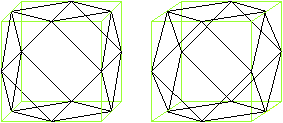
You can recognize that the cuboctahedron can develop from a (green)
cube. You connect the centres of the cube edges. Thus eight pyramids arise,
which you must cut off. The remaining solid is the cuboctahedron.
The cube is called " the producing cube" on this page.
Special Views top
Variables of the Cuboctahedron
top
The length of the edge of the cuboctahedron is
given as a.
Then you can calculate the Radius R of the circumscribed
sphere, the volume V, the area O, the distance d3 of the
triangles, and the distance d4 of the squares.
There is
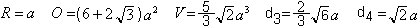
Derivations
Area
If a is the length of the edge of the cuboctahedron, the surface ist
O=6*a²+8*(1/4)sqrt(3)a²=[6+2sqrt(3)]a².
You use the area formulas A=(1/4)sqrt(3)a² of the equilateral
triangle and A=a² of the square.
Volume
The producing cube has the edge length sqrt(2)a.
Subtract the volumes of the eight triangle pyramids from the volume
of the producing cube.
Volume of the pyramid
|
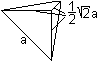
The formula is V=base*height/3. The triangle in front is chosen as
the base.
There is V'=(a²/4)*[(1/2)sqrt(2)a]/3=(1/24)sqrt(2)a³. |
Thus the volume of the cuboctahedron is V=2sqrt(2)a³-8V' = 2sqrt(2)a³-8(1/24)sqrt(2)a³
= (5/3)sqrt(2)a³.
Thickness
Two squares lie in opposite to each other.
Their distance is d1=sqrt(2)a.
Two triangles lie in opposite to each other.
Their distance d2 is the length of the space diagonal of
the cube sqrt(3)[sqrt(2)a]=sqrt(6)a, decreased by the double height of
the corner pyramid. The height h is related to the base "eqilateral triangle".
There is V'=[(1/4)sqrt(3)a²]h/3=(1/12)sqrt(3)a²h or V'=(1/24)sqrt(2)a³
(see above) for the volume of the triangle pyramid. Thus there is h=(1/6)sqrt(6)a.
The searched distance is d2=sqrt(6)a-2(1/6)sqrt(6)a = (2/3)sqrt(6)a.
Circumscribed sphere
R
|
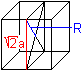
There is only drawn the producing cube.
You see R=a. |
If you know the hexagons inside the cuboctahedron, R=a is simpler
to be seen (below).
Inscribed sphere
There is no inscribed sphere. It has to touch
all squares and triangles. But the distances are different.
Properties top
Building an octahedron.
You can put together all eight triangle pyramids, which were cut off
the producing cube. They fit the cube.
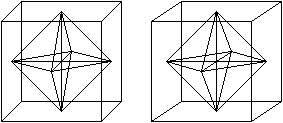
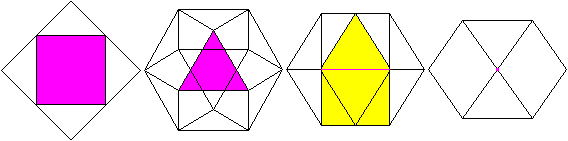
Hexagons
There are pairs of triangles at the cuboctahedron.
In the middle planes there are regular hexagons as borders.
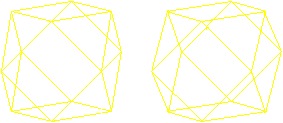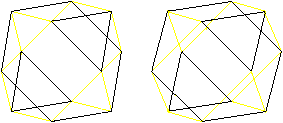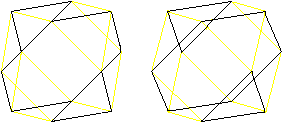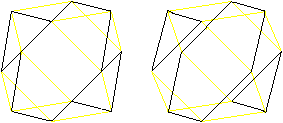
There are four different hexagons.
Now you see, why a circumscribed sphere exists. Its centre is the centre
of the cuboctahedron, the radius is the edge
length.
Closest packing of
spheres
If you lay around one (red) sphere six equal
spheres and lay in the dips three more spheres above and below, then the
centres of the (grey) spheres are the corners of a cuboctahedron.
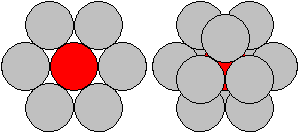
This leads to the closest packing of spheres in space. 12 spheres touch
a central sphere.
In 2D six circles touch a central circle. 24 hyperspheres touch a central
hyperspheres in the fourdimensional case.
Numbers like 6,12,24 are called "kissing numbers".
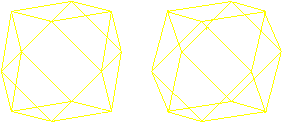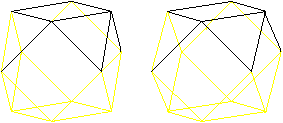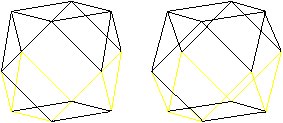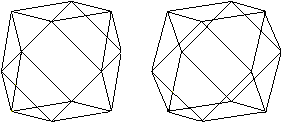
Euler's path
Four edges meet at the corners of the cuboctahedron. Therefore it is
possible to follow the edges, so that you use the edges once only.
You find more on my page House of Santa Claus.
Net top
If you spread out the cuboctahedron, you
get the following net from six squares and eight triangles. This is one
example.
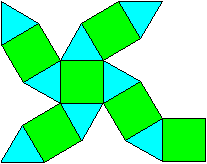
You see:
|
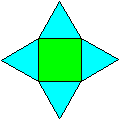
Every square is surrounded by four equilateral triangles. |
|
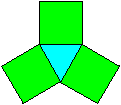
Every triangle is surrounded by three squares. |
There is a template in the book (1) "M.C.Escher
Kaleidozyklen".
Rainbow Cube top
... ... |
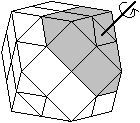The cuboctahedron has become a puzzle similar to Rubik's Cube. It is
from Japan.
There are middle planes between the two triangles and the hexagon. Thus
you get a slice to every triangle, which you can turn around an axis, which
goes through the centre of the cubeoctahedron and is perpendicular to the
triangle.
On the left there is one of the eight slices drawn in grey. |
... ... |
The surface of the cuboctahedron is coloured in a similar way to Rubik's
Cube. Opposite areas have the same colours.
If you turn some of the eight slices, the puzzle is out of order. There
is the aim now to reproduct one colour for all squares and triangles. |
This is the puzzle:
Cuboctahedron on the
Internet top
English
Eric W. Weisstein (MathWorld)
Cuboctahedron,
Archimedean
Solid, Kissing
Number
Eric Swab
Why This Site?,
Archimedean
Polyhedra
George W. Hart
Virtual
Polyhedra (The Encyclopedia of Polyhedra)
Gijs Korthals Altes
Paper model
Cuboctahedron
H. B. Meyer (Polyhedra plaited with paper strips)
Cuboctahedron
Jaap Scherphuis
Rainbow Cube
Kenneth James Michael MacLean
THE CUBEOCTAHEDRON
Poly
A program for downloading
(Poly is a shareware program for exploring and constructing polyhedra)
Ulrich Reitebuch
Cubeoctahedron
Wikipedia
Cuboctahedron,
Truncated
cuboctahedron
German
Claus Michael Ringel
Kuboktaeder
Geneviève Tulloue ( Figures Animées pour la Physique )
Truncated
Cube and Cuboctahedron (Applet)
H. B. Meyer (Polyeder aus Flechtstreifen)
Kubo-Oktaeder
Horst Steibl
Erzeugung
von archimedischen Körpern aus Tetraeder, Würfel, Oktaeder durch
Kappen der Ecken und Kanten
Natalie Wood, Christoph Pöppe
Platonische
Körper
Wikipedia
Kuboktaeder,
Archimedischer
Körper, Großes
Rhombenkuboktaeder
References
top
(1) Doris Schattenschneider und Wallace Walker, M.C.Escher Kaleidozyklen,
Köln 1992
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
http://www.mathematische-basteleien.de/
©
2004 Jürgen Köller
top |
