What is the House of Santa Claus?
The house of Santa Claus is an
old German drawing game for small children.
... ... ... |
You have to draw a house in one
line.
You must not lift your pencil while
drawing. You must not repeat a line. During drawing you have to say: "Das
ist das Haus des Nikolaus" (="This is Santa Claus' house.").
You must speak a syllable of this
sentence for every straight line. |
Girls must know:
"Wer dies nicht kann, kriegt keinen Mann [="Who can't
do this drawing, will get no man"].
|
There is also a saying for two houses:
Das ist das Haus vom Ni-ko-laus
und ne-ben-an vom Weih-nachts-mann. |
This is the house of Santa Claus
and next door of Father Christmas. |
|
... ... ...
|
Wer <N>ach-ge-<DACH>t <Z>uvor am Start,
der kennt den Weg von Le-on-hard! |
Sent by Gerald Fischböck from
Vienna |
He also added a translation:
This is <N>o <CHEVRON>, nor a piece of <Z>ulu
art,
Here comes *a lan-tern made by Le-on-hard.*
(Please start drawing with *)
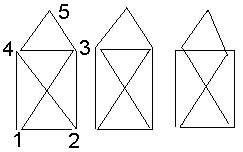
Number of the Houses
Three Examples
 ... ... |
Everybody, who knows the problem,
has a solution in his mind and can draw a house.
The question is:
How many ways are there for drawing
a house? |
Notation of
a Solution
You can write a solution as a sequence
of numbers. You number the corners of the house as shown in the left drawing.
The three houses above have the
descriptions
142354312, 145321342, 143213542.
You can record a solution by a
number with nine digits.
There are 44
Houses
The computer (C64 nostalgia) checked
all numbers between 111 111 111 and 155 555 552, whether they are a solution
or not. The computer found 44 possibilities of drawing a house:
1,2,3,1,4,3,5,4,2
1,2,3,5,4,3,1,4,2
1,2,4,5,3,1,4,3,2
1,3,2,4,5,3,4,1,2
1,3,4,2,3,5,4,1,2
1,3,5,4,2,1,4,3,2
1,4,2,1,3,5,4,3,2
1,4,3,2,1,3,5,4,2
1,4,5,3,1,2,4,3,2 |
1,2,3,1,4,5,3,4,2
1,2,4,1,3,4,5,3,2
1,2,4,5,3,4,1,3,2
1,3,4,1,2,3,5,4,2
1,3,4,5,3,2,1,4,2
1,3,5,4,2,3,4,1,2
1,4,2,3,4,5,3,1,2
1,4,3,2,4,5,3,1,2
1,4,5,3,2,1,3,4,2 |
1,2,3,4,1,3,5,4,2
1,2,4,1,3,5,4,3,2
1,3,2,1,4,3,5,4,2
1,3,4,1,2,4,5,3,2
1,3,4,5,3,2,4,1,2
1,3,5,4,3,2,1,4,2
1,4,2,3,5,4,3,1,2
1,4,3,5,4,2,1,3,2
1,4,5,3,2,4,3,1,2 |
1,2,3,4,5,3,1,4,2
1,2,4,3,1,4,5,3,2
1,3,2,1,4,5,3,4,2
1,3,4,2,1,4,5,3,2
1,3,5,4,1,2,3,4,2
1,3,5,4,3,2,4,1,2
1,4,3,1,2,3,5,4,2
1,4,3,5,4,2,3,1,2
1,4,5,3,4,2,1,3,2 |
1,2,3,5,4,1,3,4,2
1,2,4,3,5,4,1,3,2
1,3,2,4,3,5,4,1,2
...
1,3,5,4,1,2,4,3,2
1,4,2,1,3,4,5,3,2
1,4,3,1,2,4,5,3,2
1,4,5,3,1,2,3,4,2
1,4,5,3,4,2,3,1,2 |
All sequences start in 1 and end in 2. You can conclude
that there are also 44 houses starting in 2 and ending in 1. They are the
same because of their symmetry.
All Houses
Start at the Bottom
There are three lines coming together
in 1 and 2. But there are four lines coming together in 3 and 4. You have
only two lines in 5.
So you must go through 3 and 4
twice and through 5 once. You must go through 1 and 2 once, but also start
or end.
Euler Path top
The "house of Santa Claus"
is more than a simple children's game. The next statements show it.
For historical reasons I will start
with the Königsberger bridge problem (Königsberg is at the river
("old and new") Pregel. It was the capital of Ostpreußen before 1945
and is now called Kalingrad.).
The Swiss mathematician Leonhard Euler (1707-1783) worked
on this problem and solved it.
...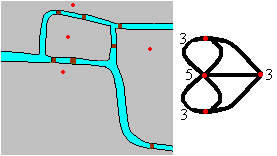 ... ... |
The problem is to find a way through Königsberg,
so that you cross all seven bridges not more than once. Is it possible?
You can simplify the locality by a graph of four points
with lines as paths. |
Euler found out, that a tour starting in one point and returning
to the same point is not possible because of the odd numbers of paths.
He generalized to his theorem: A tour this way is only possible, if all
the numbers of paths passing a point are even.
The problem of "The Seven Bridges of Königsberg"
is the origin of an important branch of mathematics, the Graph Theory as
a part of the Discrete Mathematic.
In the terminology of the Graph Theory a point is a vertex
and a path is an edge. The whole figure is a network. Every vertex has
a valence. This is the number of edges, which meet at a vertex. If the
tour begins and ends in the same vertex, you have an Euler circle, otherwise
an Euler path.
So Euler's theorem says: An Euler circle is only possible,
if the valences of all vertices are even.
... ... ... |
If you look at the house of Santa Claus again, you realize
that there is no Euler circle because of the two lower vertices with the
valence 3. But there is an Euler path beginning and ending below. |
By the way the network is planar, because you can draw it
in such a way that the edges don't cross (drawing). It is not complete,
because not all possible edges are drawn.
Hamilton Path top
There is a second problem. You don't watch the edges,
which you must pass once. You must go through the vertices once. These
paths are called Hamilton paths. If the journey is closed, you have Hamilton
circles, otherwise Hamilton paths.
Euler worked on a second popular problem, which needs
Hamilton circles, the knight's tour.
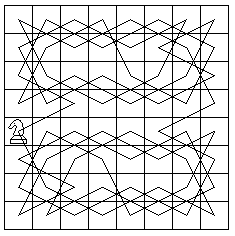 |
You are to move a knight on the chessboard, so that each
field is passed once and it returns to the start.
You look for an Hamilton circle. The vertices are the
centres of the squares of the chessboard. The Hamilton paths use two edges,
which meet in a vertex.
There are thousands of paths for the knight's tour. Actually
all tours are handsome.
There is one of Euler's solutions on the left. |
Three paths
...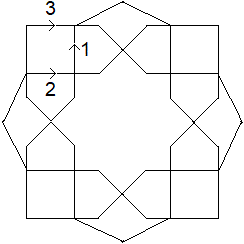 ... ... |
After three rounds, the figure is finally created by
a closed curve.
You start in 1, passes 2 and end in 3. |
... ... ... |
The best way to create the figure is to use a dot pattern.
You get a large square by placing small squares in the
corners and in between them half a square, a square and a half square in
this order. The large square gets four more points by mirroring the centers
of the small square.
The points are connected appropriately. |
The figure sent Volker Sayn.
Curves controlled by points. can be found on my website
Kolams
and Sona.
More Figures top
... .... .... |
There were two houses drawn separated above.
You can leave out a wall. Then the saying is "Das
ist das Haus vom Ni-ko-laus, ne-ben-an vom Weih-nachts-mann" (=This is
the house of Santa Claus, next door of Father Christmas.). This figure
is insoluble. There are four vertices with odd valences. |
If you remove the common wall, it is soluble again.
You find out (internet makes it possible!),
that the house of Santa Claus is nearly unknown in English speaking countries.
Sometimes it is called a purse or an envelope.
There are many figures instead, which admit Euler circles.
Here are some examples.

... ... ... |
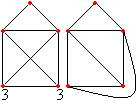
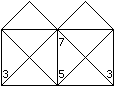
Looking for Euler circles is easier, if you colour the
figures in grey and white.
This proves the solution of Lewis Carrol's problem with
three squares on the left. |
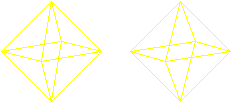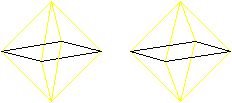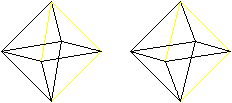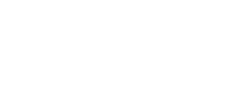
There are also Euler and Hamilton
paths in 3D-figures.
You can choose the octahedron as an example, where four
edges meet in a vertex.
If you succeed in the 3D-view, you see the octahedrons
three-dimensional.
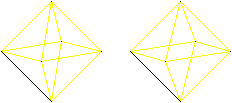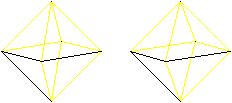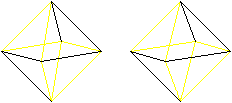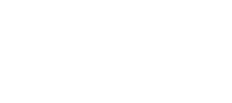
Hamilton circle
You can illustrate the Hamilton circle with a employee of
a parcel post, who must deliver the parcel to one customer (=vertex) after
the other. |
....... |
Euler circle
You can illustrate the Euler circle with a postman, who passes
definite streets (=edges) every day to deliver the post.
. |
Bonus: Cubeoctahedron and
square antiprism
Drawings in one
(closed) Line
top
1st Example:
.........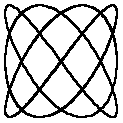 .............. .............. |
There are Lissajous figures, whose lines have no beginning
and no end. They are well known in physics and mathematics.
You find more similar lines on my website Egg
curves or my German page Spirograph. |
2nd Example:
Advertising doesn't miss this playing with lines. (Thank
you, Redzep)

|
It is situated at Bodenheim. |
3rd Example:
You find many examples in art.
There are Pablo Picasso's dog or peace pigeon drawings.
However he didn't follow the principle of the closed
line exactly.
There are also examples by Paul Klee.
Drohender Schneesturm (1927), Kleiner Narr in Trance
(1927),
Altes Fräulein (1931) (developed by an unwinded
thread)
I tell them without showing the drawings because of the
copyright.
Arabesques from Andalusia/Spain from
the Moor times are impressive. Here is an example.

The template of this drawing is on a tile bought in the
tourist shop of the Real Alcazar in Sevilla.
Three Old Writing
Games top
Houses
This is a competitive drawing game for children called
"houses".
...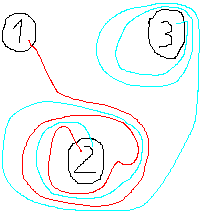 ... ... |
You spread out ten houses on a sheet of paper. You symbolize
them by circles with numbers. One player after the other must connect the
houses by lines (=paths). They must not touch the already drawn paths or
even cross them. You get a penalty point for every contact. If there is
a touch, the following players can use it as a crossing without getting
penalty points.
The drawing on the left shows that the players are older,
because there are already harassments in form of spirals. |
Probably I shouldn't make the following statement because
of possible imitating. But I do: You must have one hair torn for every
penalty point ;-(.
Two nice drawing games for
small children still unable to draw are following. You tell them a story
while drawing.
Shopping

|
Mrs. Meier,
two eggs, one sausage, one comb.
Please surround them
with two handles to carry.
Some pins,
one matchbox,
one big cake with raisins inside,
one broom, one scrubber. -
It makes 66 altogether. |

|
Fetching
Milk
Here is another game also passed down generations.

|
A girl looks out of the window. There is the milkman.
She fetches milk.
She runs, stumbles and stands up (1st leg).
She runs further.
She stumbles again, falls down and stands up again (2nd
leg).
She pours out the milk (spiral tail)
and runs home (back). |
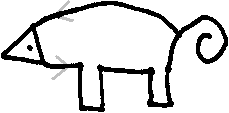
|
If you don't recognize the animal, it is a pig ;-).
References
(German only)
top
(1) Hermann Schubert: Mathematische Mußestunden,
Berlin 1941
... ... ... |
Als mir dieses Buch in die Hände fiel, versah ich
den ersten Satz dieser Seite doch lieber mit einem Fragezeichen. (Das
Haus des Nikolaus ist ein uraltes (?) deutsches Zeichenspiel für kleine
Kinder.)
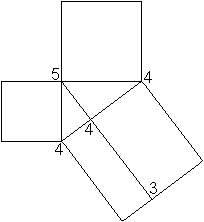
Im Kapitel Eulersche Wanderungen
wird auch ein Figur gezeigt, die wie beim Haus vom Nikolaus keine
Eulerkreise, wohl aber Eulerwege zulässt. Die Figur links ermöglicht
es, den Satz des Pythagoras zu beweisen.
Wäre Schubert das Haus vom
Nikolaus bekannt gewesen, hätte er diese ungewöhnliche Figur
wohl durch das Haus ersetzt.
Wenn ich zurückdenke, ich
lernte das Nikolaushaus in den 1940er / 1950ger als Kind kennen. |
(2) Will Grohmann, Paul Klee,
Handzeichnungen, Köln 1959
(3) Martin Gardner: Mathematisches Labyrinth, Braunschweig/Wiesbaden
1979 [ISBN 3-528-08402-2]
(4) Monika Dewess, Günter Dewess (Hrsg.): Summa
Summarum, Thun / Frankfurt/Main 1986 [ISBN 3-87144-898-2]
(5) Peter Gritzmann, René
Brandenberg: Das Geheimnis des kürzesten Weges, Springer Berlin...,
2002
[ISBN 3-540-42028-2]
I mention the book for two reasons. It contains a link
to this page :-). On the other hand, it is a good introduction to discrete
mathematics (especially graph theory). Reading the book, it becomes clear
that this relatively new field of research has applications in many areas
of our reality.
The
House
of Santa Claus on the Internet top
English
Behance
One-line-Animal-logos
Eric W. Weisstein (MathWorld)
Eulerian
Cycle
Torsten Sillke
Counting
Eulerian Circuits and Tours
Wikipedia
Eulerian
path,
Seven
Bridges of Königsberg, La
Linea , Space-filling
curve, Glossary
of graph theory
German
Dirk Brundelius
Das ist das
Haus vom Nikolaus (alle 44 Häuser als "animated Gifs")
Klaus Huneke
Dies
ist das Haus vom Nikolaus, Acryl auf Nessel, Startseite
Lutz Tautenhahn
Nikulus
Wikipedia
Haus
vom Nikolaus,
Eulerkreisproblem,
Hamiltonkreisproblem,
Königsberger
Brückenproblem, La
Linea, FASS-Kurve,
Glossar
Graphentheorie
Gail from Oregon Coast, thank
you for supporting me in my English.
Feedback: Email address
on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |