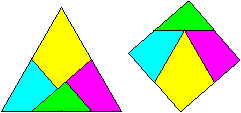|
Was sind Uhren-Aufgaben?
... ... ... |
Uhren-Aufgaben sind Denksportaufgaben, die vom Ziffernblatt
einer Uhr und den Zeigern handeln.
Dabei werden ideale Uhren vorausgesetzt, also Uhren, deren
Zeiger sich nicht wie üblich schrittweise weiter bewegen, sondern
stetig. |
Viele Aufgaben sind Klassiker der Unterhaltungsmathematik.
Neun Aufgaben
werden gestellt top
1) Zeiger liegen übereinander
Um 12 Uhr zeigen der große
und der kleine Zeiger nach oben.
Wann liegen die beiden Zeiger wieder
übereinander?
Quelle: (2) Problem 43
2) Zeiger bilden
eine Strecke
Um 6 Uhr zeigt der große
Zeiger nach oben, der kleine nach unten.
Wann bilden die beiden Zeiger wieder
eine Gerade?
3)
Winkel zwischen den Zeigern
Gegeben ist die Zeit 12:44 Uhr.
Welchen Winkel bilden die beiden Zeiger?
4)
Zeiger stehen aufeinander senkrecht
Um 3 Uhr bilden der große
und der kleine Zeiger einen rechten Winkel.
Wann bilden die beiden Zeiger wieder
einen rechten Winkel?
5)
Drei Zeiger liegen übereinander
Um 12 Uhr liegen der große,
der kleine und der Sekundenzeiger übereinander. Wann passiert dieses
Ereignis wieder?
6)
Zeiger vertauschen
Bei welchen Zeigerstellungen werden
Zeiten angezeigt, die auch Uhrzeiten bedeuten, wenn man den Minuten- und
den Stundenzeiger austauscht?
Quelle: (1) Problem 61
7)
Vierteilung des Ziffernblattes
...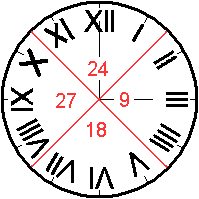 ... ... |
Das nebenstehende Ziffernblatt ist in vier Flächen
aufgeteilt. In jeder ist die Summe der dort liegenden Zahlen eingetragen.
Wie muss man das Ziffernblatt aufteilen, damit in jeder
Teilfläche die gleiche Summe erscheint?
(3) |
8) Weg der Zeigerspitze
Der große Zeiger einer Armbanduhr
hat die Länge von 1cm. Welchen Weg legt die Zeigerspitze in einem
Jahr zurück?
9)
Himmelsrichtung mit der Uhr
Wie kann man bei Sonnenschein die
Richtung Süden mit einer Uhr feststellen?
Quelle: Volksgut
Weitere
Aufgaben findet man z.B. als Aufgabe 57 bis 66 bei (1) im Kapitel Clock
Puzzles.
1) Zeiger
liegen übereinander --- Lösung top
Um 12 Uhr zeigen der große
und der kleine Zeiger nach oben. Wann liegen die beiden Zeiger wieder übereinander?
Erste
Lösung
Wenn der große Zeiger einmal das Ziffernblatt umkreist,
hat er einen Winkel von 360° überstrichen. In dieser Zeit hat
sich der kleine Zeiger um eine Ziffer weiter bewegt, also um einen Winkel
von 30°. Der große Zeiger ist also 12mal schneller als der kleine
Zeiger.
Ausgangszeit ist 12 Uhr. Der große und der kleine
Zeiger decken sich. Bei einem vollen Umlauf des großen Zeigers in
einer Stunde hat sich der kleine Zeiger um 1/12 weiter bewegt. Um ihn zu
erreichen, muss der große Zeiger um 1/12 weiterdrehen. Dann ist der
kleine Zeiger aber um 1/12 von 1/12, also um 1/12² weitergewandert.
Dem muss der große Zeiger folgen. Wieder bewegt sich der kleine Zeiger
um 1/12 von 1/12² weiter, der große folgt und so fort.
Der große Zeiger bewegt sich also um 1+1/12+1/12²+1/12³+...
weiter.
Das ist eine Summe mit beliebig vielen Summanden. Meist
geht sie über alle Grenzen. In diesem Falle nähert sie sich einem
Grenzwert.
Da es sich hier um eine geometrische Reihe mit a0=1
und q=1/12 handelt, ist er bekannt: s=a0/(1-q)=12/11.
Der große Zeiger bewegt sich also um 12/11 Stunden
weiter, also um 1/11 mehr als um eine volle Drehung.
1/11 von 60 Minuten sind 60/11 min. Es gilt weiter 60/11
min=5 min + 27 s + 3/11 s.
Ergebnis: Zum Zeitpunkt 13:05:27 und 3/11s stehen die
beiden Zeiger wieder übereinander.
Zweite
Lösung
Der große Zeiger läuft 12mal schneller als
der kleine Zeiger.
Der große Zeiger überstreicht in der Zeit
t den Winkel 360*t Grad, der kleine 30*t Grad.
Übereinstimmung der Zeiger ist gegeben, wenn gilt
30t =360t-360n oder t=(12/11)n.
n ist die Anzahl der Umdrehungen.
Der große Zeiger bewegt sich also für n=1
um 12/11 Stunden weiter, also um 1/11 mehr als um eine volle Drehung.
1/11 von 60 Minuten sind 60/11 min. Es gilt weiter 60/11
min=5 min + 27 s + 3/11 s.
Ergebnis: Zum Zeitpunkt 13:05:27 und 3/11s stehen die
beiden Zeiger wieder übereinander.
Verallgemeinerung
Für das n-te Treffen gilt (1/12)t = t - n oder t=(12/11)n.
Zu folgenden Zeitpunkten liegen die Zeiger übereinander.
n= 01
n= 02
n= 03
n= 04
n= 05
n= 06
n= 07
n= 08
n= 09
n= 10
n= 11
|
12/11
24/11
36/11
48/11
60/11
72/11
84/11
96/11
108/11
120/11
132/11
|
1:05:27 Uhr und 3/11s
2:10:54 Uhr und 6/11s
3:16:21 Uhr und 9/11s
4:21:49 Uhr und 1/11s
5:27:16 Uhr und 4/11s
6:32:43 Uhr und 7/11s
7:38:10 Uhr und 10/11s
8:43:38 Uhr und 2/11s
9:49:05 Uhr und 5/11s
10:54:32 Uhr und 8/11s
12:00:00 Uhr |
|
2) Zeiger
bilden eine Strecke --- Lösung top
Um 6 Uhr zeigt der große
Zeiger nach oben, der kleine nach unten.
Wann bilden die beiden Zeiger wieder
eine Gerade?
Lösung
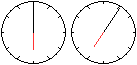
|
Hier trifft - leicht abgeändert - die Lösung
der Aufgabe 1 zu. Die Zeit ist 7:05:27 und 3/11s. |
3)
Winkel zwischen Zeigern --- Lösung top
Gegeben ist die Zeit 7:17 Uhr.
Welchen Winkel alpha bilden die beiden Zeiger?
Lösung
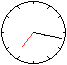 |
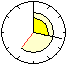 |
Der Winkel zwischen der nach oben gerichteten Vertikalen
und dem großen Zeiger ist 17*6°.
Der Winkel zwischen der Vertikalen und dem kleinen Zeiger
ist 7*30°+(17/60)*30°. |
Der gesuchte Winkel alpha ist gleich der Differenz der beiden
Winkel.
alpha=[7*30°+(17/60)*30°]-17*6° = 116,5°
Verallgemeinerung
Die Zeit sei hh:mm. Es gilt hh*30°+(mm/60)*30°-mm*6°
=hh*30°-mm*5,5°.
Der Winkel zwischen den Zeigern ist gleich dem Betrag
des Terms: alpha=|hh*30°-mm*5,5°|.
4)
Zeiger stehen aufeinander senkrecht --- Lösung top
Um 3 Uhr bilden der große
und der kleine Zeiger einen rechten Winkel.
Wann bilden die beiden Zeiger wieder
einen rechten Winkel?
Lösung
...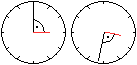 ... ... |
Es wird die Formel aus Aufgabe 3 vorausgesetzt: alpha=|hh*30°-mm*5,5°|.
Es soll mit hh=03 gelten: 90°=5,5°*mm -3*30°.
Daraus folgt 5,5°*mm=180° oder mm=180/5,5=360/11=32+8/11.
Ergebnis: Der nächste Zeitpunkt ist 3:32:43 und
7/11s. |
5)
Drei Zeiger liegen übereinander --- Lösung top
Um 12 Uhr liegen der große,
der kleine und der Sekundenzeiger übereinander. Wann passiert dieses
Ereignis wieder?
In Aufgabe 1 (zweite Lösung) wird gezeigt, dass
der
Minuten- und der Stundenzeiger zur Zeit t=(12/11)n übereinander
liegen. Das folgt aus dem Ansatz 30t =360t-360n.
Jetzt kommt noch der Sekundenzeiger hinzu.
Der Sekundenzeiger läuft 60-mal schneller als der
Minutenzeiger und 720-mal schneller als der Stundenzeiger.
Der Stundenzeiger überstreicht in der Zeit t
30t Grad, der Minutenzeiger 360t Grad und der Sekundenzeiger 21600t Grad.
Der Minuten- und der Sekundenzeiger stimmen überein,
wenn 360t-360n=21600t-360m gilt (n und m sind ganze Zahlen).
Aus 360t-360n=21600t-360m folgt t=(1/59)(m-n).
Bei Übereinstimmung aller Zeiger muss gelten: t=(12/11)n
/\ t=(1/59)(m-n) oder 719n=11m.
Diese Gleichung ist in ganzen Zahlen m und n nicht lösbar,
schon da 11 und 719 Primzahlen sind.
Ergebnis: Nur um 12 Uhr liegen die Zeiger übereinander.
Bei Dr. Math (URL unten)
kann man noch weiter nachlesen: "One could ask for the closest bunching
not at 12 o'clock. I find that this occurs at about 5:27:27.3, when all
the hands are within a 1.0014 degree sector."
6)
Zeiger vertauschen --- Lösung top
Bei welchen Zeigerstellungen werden
Zeiten angezeigt, die auch Uhrzeiten bedeuten, wenn man den Minuten- und
Stundenzeiger austauscht?
Lösung
In (1) wird nach den Zeigerstellungen zwischen 15 Uhr
und Mitternacht gefragt und dafür werden 66 Zeit-Paare angegeben.
Eine nachvollziehbare Lösung bietet Manfred Börgens
im Internet an (URL unten).
Er findet 143 Zeit-Paare. Darunter sind die 11 Stellungen,
bei denen beide Zeiger übereinanderliegen.
Ist x die Zeigerstellung des Stundenzeigers, so gilt x
= (12/143)j (j = 0,1,2,...,142).
7)
Vierteilung des Ziffernblattes --- Lösung top
... ... ... |
Das nebenstehende Ziffernblatt
ist in vier Flächen aufgeteilt. In jeder ist die Summe der dort liegenden
Zahlen eingetragen.
Wie muss man das Ziffernblatt aufteilen,
damit in jeder Teilfläche die gleiche Summe erscheint?
(3) |
Lösung
...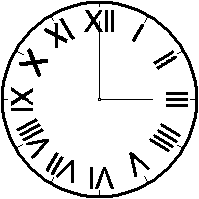 ... ... |
Das Ziffernblatt einer Uhr hat, wenn sie mit römischen
Ziffern versehen ist, üblicherweise das nebenstehende Aussehen. Die
Zahlen werden von innen aus gelesen. Die Vier wird als IIII und nicht als
IV geschrieben. Warum das so ist, ist ungeklärt.
Zählt man die Werte zusammen, erhält man 1+2+...+12=78.
Ordnet man die Ziffern um, erhält man XXXXVVVVIIIIIIIIIIIIIIIIIIII.
Das ergibt den Wert 40+20+20=80.
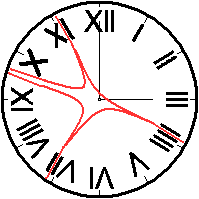
Für eine Lösung kann man auch auf die Summe
80 kommen, wenn man bestimmte zusammengesetzte Darstellungen einer Zahl
aufteilt. Das geschieht in den nächsten beiden Bildern. |
... ... ... |
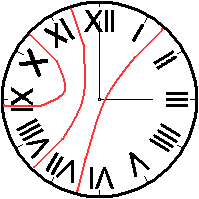 ... ... |
Die beiden Lösungen findet man in Martin Gardners
Buch "Mathematischer Karneval" auf den Seiten 231ff. unter dem Namen Cooks
(frei übersetzt: Irrtümer).
Sie wurden von den beiden Pionieren der Unterhaltungsmathematik
angegeben, von Dudeney (links) und Loyd.
Ein Schönheitsfehler in Dudeneys Lösung liegt
darin, dass man die IX von außen lesen muss, damit sie zu XI wird.
Gardner merkt noch an, dass Loyd mindestens 12 weitere
Lösungen übersehen hat. |
Anmerkung:
Hier ist eine Stelle, einmal auf die beiden "Rätselerfinder"
Sam Loyd (1841-1911) aus den USA und Henry Ernest Dudeney (1857-1930) aus
England einzugehen.
Beide waren Zeitgenossen und Berühmtheiten in ihrer
Zeit. Dudeney war unter den beiden Puzzle-Experten derjenige mit den größeren
mathematischen Fähigkeiten, Sam Loyd, ursprünglich nur Schachexperte,
war ein gewiefterer Geschäftsmann.
Beide standen miteinander in Kontakt. Dudeney schickte
eine große Anzahl seiner Puzzles zu Loyd, stellte das aber bald ein,
als er bemerkte, dass dieser sie unter seinem eigenen Namen veröffentlichte.
Die beiden verschiedenen Lösungen des obigen Problems
"Vierteilung des Ziffernblattes" mögen ein Beispiel dafür sein,
dass sie oft ähnliche Rätsel veröffentlichten und dass sie
sich gegenseitig zu übertreffen versuchten.
In Martin Gardners Buch (4) kann man mehr über die
beiden nachlesen:
>Sam Loyd: Amerikas größter Rätselerfinder
(Seite 40 bis 48)
>Henry Ernest Dudeney: Englands größter Rätselerfinder
(Seite 70 bis 77)
In meiner Homepage gehe ich
auf einige berühmte Puzzles von Dudeney ein:
Tangram, Zerschneidung
eines Dreiecks, Fliege-Spinne-Problem, Crescent
Puzzle, Send more money.
Sam Loyd war auf meiner Homepage
durch das Fünfzehnerspiel vertreten. Neuere Forschungen haben ergeben,
dass er nicht der Erfinder dieses Puzzles war.
8) Weg der Zeigerspitze
--- Lösung top
Der große Zeiger einer Armbanduhr
hat die Länge von 1cm. Welchen Weg s legt die Zeigerspitze in einem
Jahr zurück?
Lösung
s=(2*pi*1cm)*60*24*365=33 km (gerundet auf zwei Stellen)
9)
Himmelsrichtung mit der Uhr --- Lösung top
Wie kann man bei Sonnenschein die
Richtung Süden mit einer Uhr feststellen?
Lösung
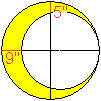
Hält man die Uhr so, dass
der Stundenzeiger auf die Sonne zeigt und halbiert dann den Winkel zwischen
dem Stundenzeiger und der gedachten Linie der 12-Uhr-Anzeige, so ist die
Halbierungslinie nach Süden gerichtet.
Uhren-Aufgaben
im Internet
top
Deutsch
Wikipedia
Samuel
Loyd,
Ernest
Dudeney
Englisch
Gary Darby
Clock
Angles
Henry Ernest Dudeney (Project Gutenberg Literary Archive
Foundation)
Amusements
in Mathematics
Wikipedia
Clock
angle problem, Henry
Dudeney, Sam
Loyd
Referenzen top
(1) Henry Ernest Dudeney: Amusements in Mathematics,
Project Gutenberg (aus dem Internet herunterladen möglich)
(2) Sam Loyd: Mathematische Rätsel und Spiele, Köln
2003 [ISBN 3-8321-1049-6]
(3) Martin Gardner: Mathematischer Karneval, Frankfurt/M,
Berlin 1977 [ISBN 3 550 07675 4]
(4) Martin Gardner: Mathematische Rätsel und Probleme,
Braunschweig 1968
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2008 Jürgen Köller
top |
 ...
... ...
...


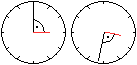 ...
... ...
... ...
...