Was ist ein Symbolrätsel?
...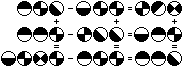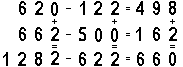 ... ...
|
Ein Symbolrätsel ist eine Anordnung von Symbolen
und Rechenzeichen. Für Symbole müssen einstellige Zahlen gesucht
werden, so dass sechs ineinander verschachtelte Gleichungen erfüllt
sind. |
Im Unterschied zu den Variablen in der gewöhnlichen
Algebra bedeuten gleiche Symbole auch gleiche Zahlen, verschiedene Symbole
verschiedene Zahlen.
Symbolrätsel sind in Deutschland bekannt und beliebt.
Es gibt eine Reihe von Zeitschriften wie STERN, GONG oder HÖR ZU,
die regelmäßig ein Rätsel dieser Art bringen (2001).
Symbolrätsel sind im englischsprachigen Raum kaum
bekannt.
Vier Beispiele
top
Man benötigt kein Spezialwissen für das Entschlüsseln
von Symbolrätseln. Wer die Grundrechenarten kennt, kann sie lösen.
Der Reiz der Symbolrätsel liegt darin, dass jedes
Rätsel in eine kleine selbstständige Zahlenwelt führt. Für
jedes Rätsel muss man sich eine neue Strategie zurechtlegen. Es gibt
keinen allgemeingültigen Lösungsweg.
Man kommt mit einer Kombination aus Probieren und logischem
Schließen zum Ziel. Es gibt ein paar Tricks, die in den folgenden
vier Beispielen vorkommen.
Beispiel 1:
top
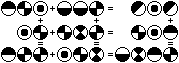 ... ... |
Das Rätsel enthält 6
Summen. Es werden 7 Symbole verwendet; also werden 7 Zahlen gesucht. |
Der erste Schritt ist die Einführung von Variablen.
Das schafft Übersicht und Vertrautheit.
In den folgenden Darstellungen werden der Einfachheit
halber die Rechenzeichen in der Vertikalrichtung nicht notiert.
abc+dde=.fcf
.cb+bge=..bca
aee+cbg=dgae... |
Wegen e+g=e in der letzten Zeile ist g=0.
 |
abc+dde=.fcf
.cb+b0e=..bca
aee+cb0=d0ae.... |
Die nächste Ziffer ist d=1. Werden zwei dreiziffrige
Zahlen addiert, so ist die Summe eine vierziffrige Zahl mit 1 an der ersten
Stelle. |
abc+11e=fcf
.cb+b0e=bca
aee+cb0=10ae |
Wegen e+e=10 ist e=5. Wegen 1+1=b ist b=2.

 |
a2c+115=fcf
.c2+205=2ca
a55+c20=10a5 |
Wegen c+2=5 ist c=3.
Wegen 2+5=a ist a=7.

 |
723+115=.f3f
.32+205=.237
755+320=1075 |
Wegen 3+5=f ist f=8.
 |
Ergebnis:
723+115=.838
.32+205.=.237
755+320=1075
Dieses Rätsel ist ein Glücksfall, da sich die
Ziffern nacheinander eindeutig ergeben.
Es gibt ein lineares Lösungsdiagramm:
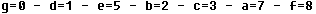
Beispiel 2:
top
...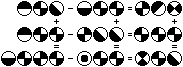 ... ... |
Das Rätsel enthält 3
Summen und 3 Differenzen. 9 Ziffern sind zu finden. |
.abc-dbb=efg
.abb-ecc=bbb
dbeb-hbb=ibc |
Wegen c+b=b ist die Ziffer c=0.
Weiter ist in der letzten Zeile d=1 (s.o).
 |
.ab0-1bb=efg
.abb-e00=bbb
1beb-hbb=ib0... |
Für a kommen wegen a+a=10+b
die Ziffern a=6, a=7, a=8 oder a=9 in Frage.
 |
a=6 wird weiter verfolgt.
.6b0-1bb=efg
.6bb-e00=bbb
1beb-hbb=ib0... |
Es sei a=6.Wegen 6+6=10+b ist b=2.
(b=3 ist wegen b+b=g nicht möglich.)
Weiter ist wegen g+b=0 (10) die
Variable g=8.. |
.620-122=ef8
.622-e00=222
12e2-h22=i20... |
Wegen 620-122=ef8 sind e=4 und f=9.
 |
.620-122=498
.622-400=222
1242-h22=i20... |
Wegen 122+400=522 ist h=5. - Wegen 498+222=720
ist i=7.
 |
Ergebnis:
.620-122=498
.622-400=222
1242-522=720.
Die Erfahrung zeigt, dass Symbolrätsel nur eine Lösung
haben. (Ich weiß, es gibt auch mehrdeutige Rätsel. Das sind
Exoten. Dieses ist die Antwort auf eine Email.) Deshalb muss man die Fälle
a=7, a=8 oder a=9 nicht weiter verfolgen. Verfolgt man sie, so gelangt
man schnell zu Widersprüchen.
Lösungsdiagramm:
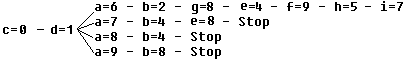
Beispiel 3:
top
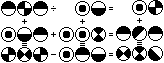 ... ...
|
Das Rätsel enthält 1 Quotienten, 4 Summen und
1 Differenz.
Es müssen 9 Ziffern bestimmt werden. |
aba :.cd=.ce
cda+ccf=aga
ehe-cad=hfi... |
Wegen d+f=d ist f=0.
 |
aba :.cd=.ce
cda+cc0=aga
ehe-cad=h0i... |
Wegen der ersten Zeile ist c=1 oder c=2 oder c=3.
Ein Produkt aus zwei zweistelligen Zahlen ist nur dreistellig,
wenn die erste Ziffer 1,2 oder 3 ist.
 |
c=1 wird weiter verfolgt.
aba :..1d=..1e
1da+110=aga
ehe-1ad.=h0i... |
Wegen 1+1=a ist a=2.
 |
2b2
:..1d=..1e
1d2+110=2g2
ehe-12d=.h0i... |
Wegen 2+2=e ist e=4.
 |
2b2 :..1d=..14
1d2+110=2g2
4h4-12d=h0i... |
Die erste Zeile wird nur durch 252=18x14 erfüllt.
.........
Damit sind b=5 und d=8.
 |
252 :..18=..14
182+110=2g2
4h4-128.=h0i... |
Wegen 4+2=i ist i=6.
Wegen 182+110=292 ist g=9. Dann ist h=3.
 |
Ergebnis:
252 :..18=..14
182+110=292
434-128.=306
Lösungsdiagramm:
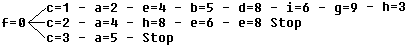
Beispiel 4:
top
...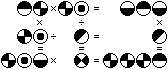 |
Das Rätsel enthält 4 Produkte und 2 Quotienten.
Man muss 7 Ziffern ermitteln. |
..ab*.bc=..dad
..ec:....f=......f
bcd*...g=bbea... |
ec ist eine Quadratzahl mit verschiedenen Ziffern.
Für f kommen f=4 oder f=7 oder f=8 oder f=9 in Frage.
 |
f=4 wird weiter verfolgt. Wegen 4*4=16 sind e=1 und c=6.
..ab*.b6=..dad
..16:....4=.....4
b6d*...g=bb1a |
Wegen 36:4=9 sind b=3 und g=9.
 |
..a3*.36=..dad
..16:....4=.....4
36d*...9=331a |
Wegen 3*6=18 ist d=8.
 |
..a3*.36=..8a8
..16:....4=.....4
368*...9=331a |
Wegen 8*9=72 ist a=2.
 |
Ergebnis:
..23*.36=..828
..16:....4=.....4
368*...9=3312
Lösungsdiagramm:
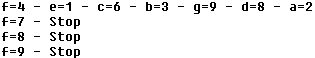
Mathematischer
Hintergrund
top
Beim Symbolrätsel handelt es sich um ein Gleichungssystem
aus 6 Gleichungen mit mehr als 6 Variablen. Nur 6 Gleichungen mit 6 Variablen
führen i.a. zu eindeutigen Lösungen. Wenn Symbolrätsel trotzdem
praktisch nur eine Lösung haben, so liegt es daran, dass nur natürliche
Zahlen als Lösung zugelassen sind ("diophantische Gleichungen") und,
das ist eine weitere Einschränkung, für verschiedene Symbole
verschiedene Zahlen, für gleiche Symbole gleiche Zahlen eingesetzt
werden müssen.
Herstellung
eigener Symbolrätsel top
Es ist leicht, Symbolrätsel nur aus Summen herzustellen.
Man gibt 4 Zahlen vor, zum Beispiel 723,115, 32 und 205, bildet die Summen
und ordnet sie zu dem Schema an.
...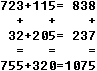 ... ... |
Dann ersetzt man die Zahlen durch
Symbole (rechts). |
...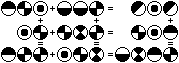 ... ... |
Das ist Beispiel 1.
Sollen Differenzen vorkommen, addiert
man negative Zahlen (Beispiel 2)
Beweis:
...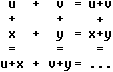 ... ... |
Das Schema links liefert den Beweis, dass Symbolrätsel
mit Summen oder Differenzen tatsächlich auf so einfache Weise zu finden
sind. Der Term, der für die drei Punkte unten rechts steht, ist gleich
(u+v)+(x+y) oder (u+x)+(v+y).
Diese beiden Terme sind gleich. |
Sollen auch Produkte oder Quotienten
vorkommen, wird es schwieriger, geeignete Anordnungen zu finden. Man sollte
den Computer einsetzen. Damit habe ich mich nicht beschäftigt.
Kryptogramme
top
Die Symbolrätsel gehören zu den Kryptogrammen.
Das sind Zahlenrätsel, die Zeichen enthalten, für die Zahlen
gesucht werden müssen, so dass eine Gleichung erfüllt wird. Man
verlangt, dass Kryptogramme
eindeutig lösbar sind.
Man beachte bei der Suche nach Kryptogrammen im Internet,
dass allgemein jede Geheimschrift Kryptogramm heißt und dass die
Informatiker heute diesen Begriff im Sinne von Verschlüsselung
neu besetzt haben.
Als Zeichen werden häufig Buchstaben verwendet, die
Worte bilden. Diese Worte ergeben dann zusammen mehr oder weniger
einen Sinn.
Diese Kryptogramme bezeichnet man als Alphametiken.
Das bekannteste Beispiel einer Alphametik ist "SEND +
MORE = MONEY"
(1000s+100e+10n+d+1000m+100o+10r+e = 10000m+1000o+100n+10e+y).
Diese Gleichung enthält acht Variable. Trotzdem gibt es nur eine
Lösung, nämlich 9567+1085=10652.
Alphametiken mit einem Sinn und vor allem einer Lösung
sind nicht leicht zu finden.
Ich habe aus Vor-Computer-Zeiten meine Alphametik anzubieten,
die "send more money" nachempfunden ist: GEHE + NACH = NAUEN. [Na ja ;-)].
Kryptogramme
im Internet top
Deutsch
Angela und Otto Janko
Alphametics
Klaus Diller
Symbolrätsel
mit Lösungen
Erik Krämer
Symbolrätsel
- die Rätsel für Zahlenfetischisten
Julia Singer
Symbolrätsel
online
Klaus Nagel
Zahlenrätsel
- Applet
Wikipedia
Mathematisches
Rätsel, Kryptogramm
Wolfgang Stanglmeier
Zahlenrätsel-Generator
Englisch
Alexander Bogomolny
Alphametics
(in der linken Spalte)
Colin Barker
Cryptarithms
(alphametics)
Mike Keith
Alphametics
The Contest Center
Collection
of alphametics
Torsten Sillke
Alphametics
Truman Collins
Alphametic
Puzzles
Wikipedia
Alphametic
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2001 Jürgen Köller
top |