|
Trio und andere Rechenspiele
|
Was ist Trio?
... ... |
... ... |
Trio*) ist ein Rechenspiel von Heinz Wittenberg für
einen oder mehrere Spieler bei einem Mindestalter von etwa 10 Jahren.
49 kleine Karten mit den Nummern 1 bis 9 werden zu einem quadratischen
7x7-Feld ausgelegt.
Gibt man zum Beispiel eine Zahl vor wie 11, so besteht die Aufgabe
darin, im Quadrat möglichst schnell eine Zerlegung der Art 11 = 3*2+5
zu finden. |
*) Copyright 1974 by Otto Maier Ravensburg
Erklärung
des Spiels top
Beschreibung
Das Spiel enthält in einer Schachtel 99 bunte Zahlenkarten, 49
quadratische und 50 runde.
Die Farben haben offenbar keine Bedeutung, sie sind Zierde.
| Die 49 quadratischen Karten tragen die Zahlen 1 bis 9 in der folgenden
Verteilung: |
 |
... ...
|
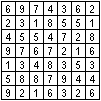Die Karten werden zu Beginn des Spiels ungeordnet zu einem 7x7-Quadrat
ausgelegt.
Dieses ist die Verteilung, die der Hersteller in seiner Anleitung vorgibt. |
Die 50 runden Karten tragen fortlaufend die Zahlen 1 bis 50. Sie werden
zu Beginn verdeckt in den Schachteldeckel gelegt.
Spielverlauf
Ein Spieler deckt zu Beginn des Spiels eine beliebige runde Karte auf,
zum Beispiel 32.
... ...
|
Jeder Spieler versucht, möglichst schnell eine Zerlegung von 32
zu finden.
Eine Zerlegung besteht aus drei Zahlen im Feld, die die Form a*b+c
oder a*b-c hat. Die drei Zahlen können nebeneinander, untereinander
oder diagonal liegen. Sie können vorwärts oder rückwärts
gelesen werden. Nebenan wird von jeder Sorte eine Zerlegung farbig gekennzeichnet.
Der Spieler, der als erster eine Zerlegung der Zahl 32 findet, nennt
sie und erhält das runde Kärtchen 32. |
Sind alle runden Karten aufgebraucht, ist das Spiel beendet. Der Spieler
mit den meisten Karten hat gewonnen.
Anmerkung: In der Spielanleitung lässt man auch ein Produkt aus
erster und dritter Zahl zu. Diese Regel habe ich auf dieser Seite nicht
berücksichtigt.
Analyse des Beispiels
Der Spielverlauf hängt von der Anordnung der quadratischen Karten
ab, die bei jedem Spiel verschieden ist.
|
......
|
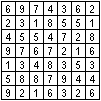Wie erwähnt wähle ich als Beispiel die Anfangskonfiguration,
die in der Spielanleitung angegeben ist. |
Mit Hilfe eines Computers habe ich diese Anordnung untersucht.. Für
die Zahl 32 z.B. gibt es 11 Zerlegungen.
|
horizontal: 32 = 5*8-8
= 9*4-4
vertikal: 32 = 9*3+5
= 5*7-3 = 5*7-3 = 5*7-3 = 6*4+8
diagonal: 32 = 6*5+2
= 7*5-3 = 4*7+4 = 4*7+4 = 5*7-3 |
Trio als Lernspiel
Trio ist ein Spiel, das in den Grundschulen verbreitet ist. Trio-Spielen
ist ein guter Weg, das kleine Einmaleins zu trainieren. Es macht darüber
hinaus Spaß.
Trio kann auch zu einem interessanten Klassenspiel werden.
Man schreibt ein 7x7-Feld aus einstelligen Zahlen an die Tafel und
teilt die Klasse in zwei Gruppen ein, z.B. in Jungen und Mädchen.
Eine Zahl um die 25 wird an die Tafel geschrieben. Dann beginnt das Suchen.
Wird eine Lösung gefunden, so dürfen die drei Zahlen mit Kreide
eingekreist werden und die betreffende Gruppe erhält einen Punkt.
Wird keine Zerlegung mehr gefunden, folgt die nächste Zahl.
Das Klassenspiel wird zu einem kostenlosen Familienspiel, wenn man
die Tafel durch einen Zettel ersetzt.
Was versteht man unter Gedachte Zahl erraten?
Es geht darum, dass sich jemand eine Zahl ausdenkt und auf Anweisungen
mit ihr rechnet und zu einem Ergebnis kommt. Der Aufgabensteller kann dann
meist zur Überraschung aller aus dem Ergebnis auf die Anfangszahl
schließen.
Beispiel:
Denke Dir eine Zahl (zum Beispiel 7); verdoppele sie; zähle 4
hinzu; halbiere die Summe; addiere 7; multipliziere das Ergebnis
mit 8; ziehe 12 ab; dividiere durch 4; ziehe 11 davon ab und gib das Ergebnis
an.
Das Ergebnis ist 18. Daraus ergibt sich die gedachte Zahl 7.
Man könnte, um von 18 zu 7 zu gelangen, die Rechenschritte umkehren.
Zu Aufgaben dieser Art gehört immer ein Trick, der die Bestimmung
erleichtert. Wie der Aufgabensteller auf die gesuchte Zahl kommt, wird
unter 01 Grundaufgabe erklärt.
Auf dieser Seite findet man weitere Aufgaben
dieser Art, die durch ein Stichwort gekennzeichnet sind, und ihren Hintergrund.
01 Grundaufgabe top
Das ist noch einmal die Aufgabe.
Denke Dir eine Zahl. Verdoppele sie; zähle 4 hinzu; halbiere
die Summe; addiere 7; multipliziere das Ergebnis mit 8; ziehe 12 ab; dividiere
durch 4; ziehe 11 davon ab und gib das Ergebnis an.
Wie oben beschrieben, ist das Ergebnis 18.
Begründung
x sei die gedachte Zahl.
Dann gilt
{[(2x+4)/2+7]*8-12}/4-11 = {[(x+2)+7]*8-12}/4-11 = [(x+9)*8-12]/4-11
= (8x+60)/4-11 = 2x+15-11= 2x+4.
Wenn 2x+4=18 ist, dann ist 2x=14 oder x=7.
Die Rechnung wird durch den Term {[(2x+4)/2+7]*8-12}:4-11 beschrieben.
Er ist durch die geschachtelten Klammern unübersichtlich. Deshalb
könnte man die praktische Notation x |*2 |+4 |:2
|+7 |*8 |-12 |:4 |-11 verwenden. Auf keinen Fall
darf man x*2+4:2+7*8-12:4-11 schreiben. Das würde zu 2x+44 führen.
02 Binomische
Formel top
Denke Dir eine Zahl. Addiere 1; quadriere die Summe; subtrahiere vom
Ergebnis das Quadrat der gedachten Zahl; addiere noch 1 und gib das Ergebnis
an.
Zahlenbeispiel: Ist 7 die gedachte Zahl, so ist das Ergebnis 14.
Begründung
x sei die gedachte Zahl.
Dann gilt (x+1)²-x²-1 = (x²+2x+1)-x²-1 = 2x.
03 Mit
unbekannter Zahl top
Denke Dir eine Zahl. Verdoppele sie und addiere irgendeine gerade Zahl;
halbiere das Ergebnis; multipliziere das Ergebnis mit 4; subtrahiere das
Doppelte von der vorher addierten geraden Zahl und gib das Ergebnis an.
Zahlenbeispiel: Die gedachte Zahl sei 5. Das Ergebnis ist 20.
Begründung
x sei die gedachte Zahl, 2n die gerade Zahl.
Dann gilt [(2x+2n)/2]*4-2*2n = (x+n)*4-2n = 4x+4n-4n = 4x
Es wird eine unbekannte Zahl n in die Rechnung eingebaut, die im Laufe
der Rechnung wieder herausfällt.
04
Aufeinander folgende Zahlen top
Denke Dir eine Zahl. Bilde die Summe dieser und der beiden darauf folgenden
Zahlen; dividiere durch 3 und gib das Ergebnis an.
Zahlenbeispiel: Ist 7 die gedachte Zahl, so ist das Ergebnis 8.
Begründung
x sei die gedachte Zahl.
Dann gilt [x+(x+1)+(x+2)]/3 = (3x+3)/3 = x+1.
05 Zwei Zahlen streichen top
Denke Dir eine Zahl. Verdoppele sie; addiere 5; multipliziere die Summe
mit 5; addiere zum Produkt 3; multipliziere die Summe mit 10; addiere 3;
subtrahiere 150 und gib das Ergebnis an.
Zahlenbeispiel: Ist 7 die gedachte Zahl, so ist das Ergebnis 833. Streicht
man die beiden Dreien weg und subtrahiert von 8 Eins, so ergibt sich die
gesuchte Zahl 7.
Begründung
x sei die gedachte Zahl.
Dann gilt [(2x+5)*5+3]*10+3-150 = (10x+25+3)*10-147 = (100x-280)-147
= 100x+100+33 = 100(x+1)+33.
06 Zehnfaches
top
Denke Dir eine Zahl. Multipliziere sie mit 50; addiere 72; ziehe vom
Ergebnis 111 ab; addiere 39; dividiere die Summe durch 5 und gib das Ergebnis
an.
Zahlenbeispiel: Ist 7 die gedachte Zahl, so ist das Ergebnis 70.
Begründung
x sei die gedachte Zahl.
Dann gilt {[(x*50+72)-111]+39}/5 = [(50x-39)+39]/5 = 50x/5 = 10x.
07
Gedachte Zahl wird Ergebnis top
Denke Dir eine vierstellige Zahl. Lass die letzte Ziffer weg; dann
die vorletzte; schließlich die drittletzte; addiere die so entstandenen
Zahlen; multipliziere die Summe mit 9; addiere die Quersumme der gedachten
Zahl und gib das Ergebnis an.
Zahlenbeispiel: Ist 1234 die gedachte Zahl, so ist das Ergebnis auch
1234.
Begründung
1000a+100b+10c+d sei die gedachte Zahl.
Dann gilt [(100a+10b+c)+(10a+b)+a]*9+(a+b+c+d) = (999a+99b+9c)+(a+b+c+d)
= 1000a+100b+10c+d
08
Immer das gleiche Ergebnis top
Denke Dir eine Zahl. Verdoppele sie; addiere 8; halbiere die Summe;
subtrahiere vom Ergebnis die gedachte Zahl und gib das Ergebnis an.
Zahlenbeispiel: Ist 7 die gedachte Zahl, so ist das Ergebnis 4.
Begründung
x sei die gedachte Zahl.
Dann gilt [(2x+8):2]-x = (x+4)-x = 4.
Für jede gedachte Zahl ist das Ergebnis 4.
09 Zwei Zahlen vorhersagen
top
Denke Dir zwei zweistellige Zahlen. Verdoppele die erste Zahl; addiere
5; multipliziere mit 50; addiere die zweite Zahl; addiere 365; subtrahiere
615 und gib das Ergebnis an.
Zahlenbeispiel: Sind 23 und 45 die gedachten Zahlen, so ist das Ergebnis
2345.
Begründung
x und y seien die gedachten Zahlen.
Dann gilt (2x+5)*50+y+365-615=100++250+y-250=100x+y.
Kommentar
zu Gedachte Zahl erraten top
Diese Seite geht hervor aus Kapiteln der mir zugänglichen Bücher
(1), (2) und (3) der Unterhaltungsmathematik.
Ich habe Aufgaben dieser Art gelegentlich als
aktiver Lehrer in der Unterstufe in Klasse 5 und 6 eingesetzt, um das Kopfrechnen
zu beleben. In diesem Alter sind die Schüler beeindruckt, weil algebraische
Kenntnisse und somit ein tieferer Einblick fehlen. Trotzdem kann sich schon
ein Aha-Erlebnis einstellen, wenn man des Spaßes halber eine Aufgabe
wie diese stellt. Denke Dir eine Zahl; addiere 5; nenne
das Ergebnis.
Es empfiehlt sich, die Schüler aufstehen
zu lassen, damit sie nicht schreiben können, und nur von einstelligen
Zahlen auszugehen, damit die Rechnungen nicht zu aufwändig werden.
Als Gedächtnisstütze hielt ich eine
Notation wie x |*2 |+4 |:2 |+7 |*8
|-12 |:4 |-11 bereit.
Referenzen top
(1) Hermann Schubert: Mathematische Mußestunden, Berlin 1941
(2) Walter Sperling: Auf du und du mit Zahlen, Rüschlikon-Zürich
1955
(3) Walter Lietzmann: Lustiges und Merkwürdiges von Zahlen und
Formen, Göttingen 1969
Weitere Zahlenspiele auf meiner Homepage: Sudoku,
Kaprekarzahl,
Symbolrätsel
Rechenspiele im Internet top
Deutsch
Angela und Otto Janko.
Rätsel, Puzzles
und anderer Denksport
Eva Börgens
Make 24 (Online-Spiel
von Manfred Börgens) |
Gegeben: 9 3 2 9 + - x / ( )
Gesucht 24=...
Eine Lösung: 24=9-3+2x9 |
Luding - die Spieldatenbank
Trio
(1989), Trio
mathekiste
Das 1999
Spiel
Wikipedia
Kuhhandel
(Spiel)
Wilhelm-Hittorf-Gymnasium Münster
Trio
(Eine Computer-Version für einen oder zwei Spieler)
Wikipedia
Trio (Spiel),
Make 24
Wolfgang Niehaus
Trio
(Spielvorlage)
Englisch
MathsIsFun
Mixed Times
Tables
Toby Gottfried
Solutions
to the 24 Game
Wikipedia
24 Game
| Number (Game)... |
Number—the player guesses a number from 1 to 100, trying to identify
the computer's target number.
"Der Computer kann ja denken." - Eines der ersten Computerspiele |
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2009 Jürgen Köller
top |