Was ist die Kaprekar-Zahl?
Die Zahl 6174 heißt Kaprekar-Zahl. 
Der indische Mathematiker D.R.Kaprekar machte im Jahre 1949 die folgende Entdeckung. 

Das 3n+1-Problem (Collatz-Problem)     top
Gegeben ist eine beliebige natürliche Zahl, aus der sich eine Folge von Zahlen nach folgenden Regeln bildet. 
Ist die Zahl gerade, so ist die nächste Zahl gleich der halben Zahl. Ist die Zahl ungerade, so wird die Zahl verdreifacht und um 1 erhöht. Das ist dann die nächste Zahl. Merkwürdigerweise erreicht diese Folge immer die Zahl 1. 

Der Steinhaus-Zyklus    top
Der Steinhaus-Zyklus heißt 145, 42, 20, 4, 16, 37, 58, 89. 
Hintergrund: 
(1) Gegeben ist eine beliebige vierstellige Zahl (abcd).
(2) Man berechnet die Summe der Quadrate ihrer Ziffern (a²+b²+c²+d²).
(3) Mit dieser Summe verfährt man ebenso und wiederholt die Rechnung.

Dieses Verfahren führt entweder auf  1 oder man gelangt unweigerlich zur Zahl 145. Dann wiederholt sich der Zyklus 42, 20, 4, 16, 37, 58, 89, 145. 

196-Problem     top
(1) Gegeben ist eine beliebige Zahl, zum Beispiel eine dreistellige Zahl (abc).
(2) Aus ihr bildet man die Spiegelzahl, indem man die Ziffern von hinten nach vorne liest (cba).
(3) Man addiert Zahl und Spiegelzahl (abc+cba).

Vielleicht ist die Summe ein Palindrom, also eine Zahl, die sich nicht ändert, auch wenn man sie von hinten nach vorne liest. 
Liegt kein Palindrom vor, addiert man zur Summe die Spiegelzahl der Summe. Vielleicht hat sich jetzt ein Palindrom ergeben. Wenn nicht, wiederholt man den Prozess. 

Fast alle Zahlen haben am Ende ein Palindrom. 

Die Zahl 1089  top
(1) Gegeben ist eine dreistellige Zahl aus nicht gleichen Ziffern (abc)..
(2) Aus ihr bildet man die Spiegelzahl, indem man die Ziffern von hinten nach vorne liest (cba)..
(3) Man bildet Unterschied zwischen der Zahl und der Spiegelzahl (|abc-cba|).
(4) Zur Differenz wird wieder die Spiegelzahl gebildet (Differenz=def, def, fed). 
.
Man addiert die beiden Zahlen und erhält 1089 (def+fed=1089).

Die Zahl 222   top
Gegeben ist eine dreistellige Zahl aus nicht gleichen Ziffern (abc). 
Man bildet 5 weitere Zahlen, indem man die Ziffern auf jede mögliche Weise umstellt (abc, acb, bac, bca, cab, cba). 
Man addiert die sechs Zahlen (abc+acb+bac+bca+cab+cba). .
Man erhält das 222-fache der Quersumme [222*(a+b+c)].

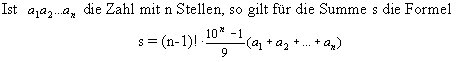Die Zahl 2997    top
Herr Pfiffig (Buch 2, Seite 75) kennt einen Trick. Er sagt: 
"Nenne drei beliebige dreistellige Zahlen (unten schwarz) ohne 0. Ich nenne auch drei dreistellige Zahlen (unten blau). Wenn wir diese sechs Zahlen addieren, ist die Summe immer 2997."
Drei Beispiele:

724 +196  +732 +803 +267 +275 ---- 2997

166 +456 +822 +177 +543 +833 ---- 2997

111 +555 +888 +888 +444 +111 ---- 2997

Erkennst du Herrn Pfiffigs Trick?

Kaprekar-Zahlen im  Internet         top

English

Alfred.Wassermann
Experiments with the 3n+1 sequence   (Applet)

Douglas E. Iannucci
The Kaprekar Numbers
6174 ist die Kaprekar-Zahl. Es gibt auch noch die Kaprekar-Zahlen. 
Beispiel: 494 und 209   (703² = 494209 und 494+209=703)

Eric W. Weisstein (world of mathematics)
Kaprekar Number     Kaprekar Routine     196-Algorithm

Math Fun Facts (Francis Su) 
Kaprekar's Constant

Terry Trotter
KAPREKAR-6174

Wikipedia
Kaprekar number, Collatz Problem, 196 problem, 

Yutaka Nishiyama
Mysterious number 6174

Alfred.Wassermann
Experiment mit der 3n+1 Folge   (Applet)

KOW’s Blog
1089

Mathetreff 
Aufgabe 1

Gomeck
Schockierende Welt der Zahlen

Wikipedia
Collatz-Problem, Lychrel-Zahl

Winfrid Krone 
Strukturen in einigen künstlichen Zahlenfolgen

Referenzen top
(1) Walter Lietzmann: Sonderlinge im Reich der Zahlen, Bonn 1948
(2) Walter Sperling: Auf du und du mit Zahlen, Rüschlikon-Zürich 1955
(3) Hugo Steinhaus, 100 Aufgaben, Urania-Verlag Leipzig, Jena, Berlin 1968