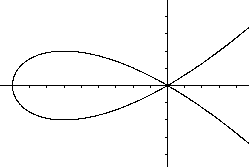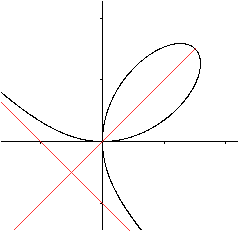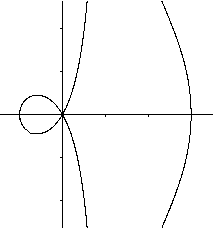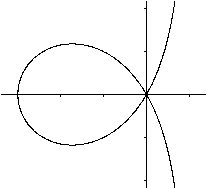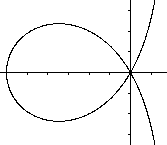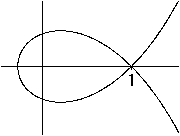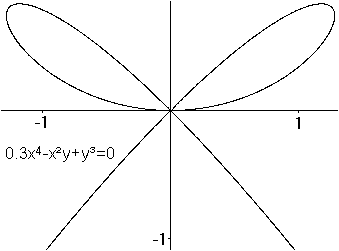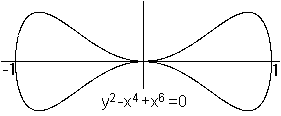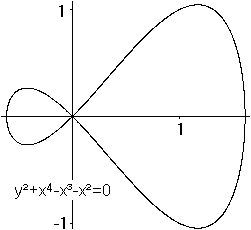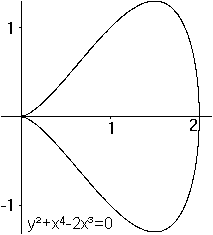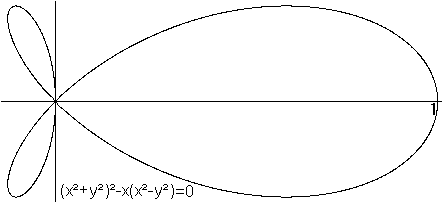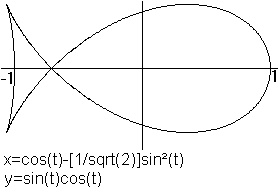Gerade Strophoide
Inhalt dieser Webseite
Was ist eine gerade Strophoide?
Zehn Eigenschaften
Geometrische Definition
Strophoide und Kreisinversion		 Weitere Kurven mit Schleifen
Strophoide im Internet
Referenzen
.
Zur Hauptseite    "Mathematische Basteleien"

Was ist die gerade Strophoide?
...... Die gerade Strophoide ist der Graph der Relation y²(a-x)-x²(a+x)=0. 

Der Parameter a steht für eine reelle Zahl. In der Zeichnung ist a=1. 

Die Gleichung y²(a-x)-x²(a+x)=0 hat die Ordnung 3.

Das Wort Strophoide kommt aus dem Griechischen. 
Strophé bedeutet Wendung, Kurve, Drehung, Biegung.

......
Man kann die Gleichung y²(a-x)-x²(a+x)=0 nach y auflösen.

Man erhält so die Strophoide als Graph der beiden Funktionen mit f1(x)=+x*sqrt[(a+x)/(a-x)] und (Bild) f2(x)=-x*sqrt[(a+x)/(a-x)].
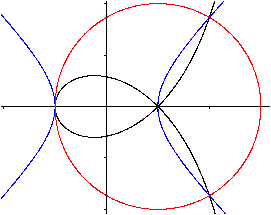
Gerade Strophoiden für einige Parameter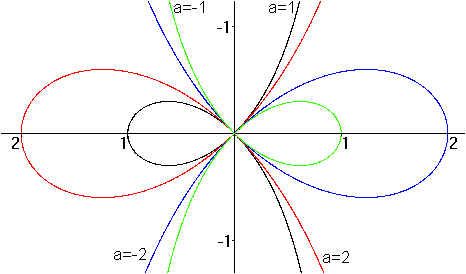
Ist a=0, so ist der Graph nur der Nullpunkt.
Neben der geraden Strophoiden gibt es auch die schiefe Strophoide.
Die schiefe Strophoide wird durch die Gleichung y²(x-a)-2x²ycos(alpha)+x²(x+a)=0
beschrieben.

In der Zeichnung ist a=1 und alpha=45°. 

Zehn Eigenschaften top
Vorweg wird die Ableitung der Teilfunktion f2(x)=-x*sqrt[(a+x)/(a-x)] oder f2(x)=-sqrt[(ax²+x³)/(a-x)] gebildet.
... Es gilt nach der Kettenregel, kombiniert mit der Quotientenregel:
f2'(x)=-(1/2)sqrt[(a-x)/(ax²+x³)]{[(2ax+3x²)(a-x)+(ax²+x³)]/(a-x)²}
f2'(x)=-(1/2)sqrt[(a-x)/(a+x)]/x{[-2x³+2ax²+2a²x]/(a-x)²}
f2'(x)=-sqrt[(a-x)/(a+x)]{[-x²+ax+a²]/(a-x)²}
f2'(x)=(x²-ax-a²)/sqrt[(a+x)(a-x)³]

(01) Der größtmögliche Definitionsbereich ist D={x|-a<=x<a}.
Für den Definitionsbereich ist entscheidend, für welche x-Werte der Term (a+x)/(a-x) positiv ist. Da gibt es zwei Fälle.
(I) a+x /\ a-x sind beide positiv. Dann ist a+x>0 /\ a-x>0 oder x>-a /\ x<a. Das bedeutet -a<x<a.
(II) a+x /\ a-x sind beide negativ. Dann ist a+x<0 /\ a-x<0 oder x<-a /\ x>a. Das ist nie erfüllt.
Der Grenzfall x=-a ist zugelassen. Ist x=a, so liegt eine Polstelle vor.
Somit ist D={x|-a<=x<a}.
Ist a<0, so führt eine entsprechende Überlegung zu demselben größtmöglichen Definitionsbereich. 
(02) Der Graph ist achsensymmetrisch zur x-Achse.
Wegen des Terms y² ändert sich die Gleichung y²(a-x)-x²(a+x)=0 nicht, wenn man y durch -y ersetzt.
(03) Der Graph hat einen Scheitelpunkt in A(-a|0).
Der Term der Relation mit y²=x²(a+x)/(a-x) hat in x=-a eine Nullstelle, und das ist ein Randpunkt.
Die Steigung, gegeben durch den Term f2'(x)=(x²-ax-a²)/sqrt[(a+x)(a-x)³], hat in x=-a auch eine Polstelle. Das bedeutet eine vertikale Tangente. Das zusammen ergibt einen Scheitelpunkt.
(04) Der Graph hat einen Hoch- bzw. Tiefpunkt an der Stelle x1=[1/2-(1/2)sqrt(5)]a.
Man benötigt die Stellen mit waagerechter Tangente, für die y'=0 ist. 
Es gilt f2'(x)=(x²-ax-a²)/sqrt[(a+x)(a-x)³].
Interessant ist, wenn x²-ax-a²=0 gilt. Dann ist x1=(1/2)a+(1/2)sqrt(5)a und x2=(1/2)a-(1/2)sqrt(5)a. 
An der Stelle x2=(1/2)a-(1/2)sqrt(5)a (angenähert -0,6a) liegen die beiden Extremstellen.
Die Stelle x1=(1/2)a+(1/2)sqrt(5)a (angenähert 1,6a) liegt außerhalb des Definitionsbereichs.
(05) Der Graph hat einen Knotenpunkt im Nullpunkt mit den Steigungen 1 und -1.
Das kann man an f2(x)=-x*sqrt[(a+x)/(a-x)] und f2'(x)=(x²-ax-a²)/sqrt[(a+x)(a-x)³] ablesen.
Es gilt f2(0)=0 und f2'(0)=-1. 
Aus Symmetriegründen hat die andere Teilfunktion f1(x)=+x*sqrt[(a+x)/(a-x)] in x=0 die Steigung +1.
(06) Die Gerade x=a ist Asymptote.
Man betrachtet wieder die Teilfunktion f2(x)=-x*sqrt[(a+x)/(a-x)].
Die Stelle x=a ist nicht definiert, wohl aber für Werte kleiner als a. 
Nähert man sich der Stelle von links, so gehen die Werte von f2(x) über alle Grenzen gegen -Unendlich. 
Aus Symmetriegründen geht f1 gegen +Unendlich.
(07) Die Strophoide wird in Polarkoordinaten durch r(t)=-a*cos(2t)/cos(t) beschrieben. 
t durchläuft die Winkel von 0 bis pi. 
Den Zusammenhang zwischen den kartesischen Koordinaten und den Polarkoordinaten beschreiben die Formeln x=r*cos(t), y=r*sin(t) und r²=x²+y². Entsprechend wird die Gleichung y²(a-x) = x²(a+x) umgeformt.
 y²(a-x) = x²(a+x)
<=>  ay²-xy² = ax²+x³
<=>  x³+xy²  = -ax²+ay²
<=>  x(x²+y²) = (-a)(x²-y²)
<=>  [r*cos(t)]*r² = (-a)r²[cos²(t)-sin²(t)]    |:[r*cos(t)]
<=>  r²={(-a)r[cos²(t)-sin²(t)]}/cos(t)     |:r
<=>  r=-a*cos(2t)/cos(t), wzbw.
(08) Eine Parameterdarstellung ist x=a(t²-1)/(t²+1) /\ y=at(t²-1)/(t²+1), wobei t alle reellen Zahlen durchläuft. 
y²(a-x) = x²(a+x)     (y=tx)
<=>  t²x²(a-x) = x²(a+x)    |:x²
<=>  t²a-t²x = a+x
<=>  t²a-at²(t²-1)/(t²+1) = a+a(t²-1)/(t²+1)   |*(t²+1)
<=>  at²(t²+1)-at²(t²-1) = a(t²+1)+a(t²-1)     |:a
<=>  t²(t²+1)-t²(t²-1) = (t²+1)+(t²-1)
<=>  t4+t²-t4+t² = t²+1+t²-1
<=>  0 = 0
Die Schlussrichtung ist von unten nach oben.
(09) Die eingeschlossene Fläche hat einen Flächeninhalt von A1=(2-pi/2)a².
(10) Die zwischen dem Graphen und der Asymptote liegende Fläche hat den Grenzwert A2=(2+pi/2)a².
In der folgenden Berechnung eines Integrals gibt es zwei Substitutionen.
1. Substitution: u=sqrt(a-x) 
Dann ist du/dx=(1/2)[-1/sqrt(a-x)], dx=-2sqrt(a-x)du, x=a-x², sqrt(a+x)=sqrt(2a-u²).

2. Substitution: sin(t)=u/sqrt(2a) oder u=sqrt(2a)sin(t)
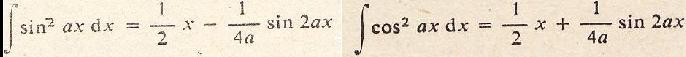Dann ist du/dt=sqrt(2a)cos(t) oder du=sqrt(2a)sin(t)dt.

Auch werden zwei Grundintegrale verwendet.

Rechnung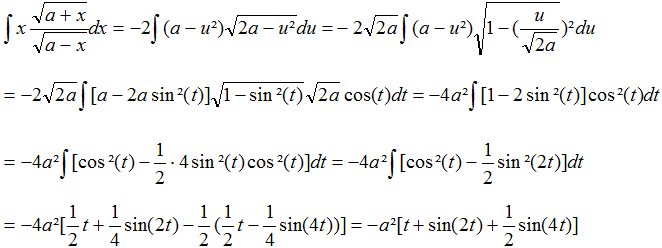
Die gesuchten Flächeninhalte sind Integrale. 
Für A1 gilt: 
Man muss noch verfolgen, wie sich die Grenzen durch die Substitutionen ändern. 
x=-a führt zu u=sqrt(a-x)=sqrt(2a) und zu sin(t)=u/sqrt(2a)=1, t=pi/2.
x=0 führt zu u=sqrt(a-x)=sqrt(a) und zu sin(t)=u/sqrt(2a)=(1/2sqrt(2), t=pi/4.

Dann ist A1=2*|(-a²)[t+sin(2t)+(1/2)sin(4t)| in den Grenzen von pi/2 bis pi/4
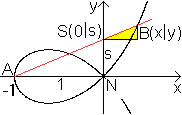
oder A1=2*|(-a²)[pi/4+sin(pi/2+0)+0-(pi/2+0+0)]|=2*(1- pi/4)a²=(2-pi/2)a², wzbw.

Für A2  gilt: 
x=0 führt wieder zu t=pi/4.
x=a führt zu u=sqrt(a-x)=sqrt(0) und zu sin(t)=u/sqrt(2a)=0, t=0.

Dann ist A2=2*|(-a²)[t+sin(2t)+(1/2)sin(4t)| in den Grenzen von pi/4 bis 0
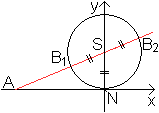
oder A2=2*|(-a²)[pi/4+sin(pi/2)+0-(0+0+0)]|=2*(1+ pi/4)a²=(2+pi/2)a², wzbw.

Quelle: http://www.stud.uni-hannover.de/~fmodler/

Geometrische Definition  top
...... Gibt man in einem kartesischen Koordinatensystem mit dem Nullpunkt N einen Punkt A auf der negativen x-Achse vor und zeichnet eine steigende Gerade, so entsteht auf der y-Achse ein Punkt S. Zeichnet man um diesen Punkt einen Kreis mit dem Radius SN, so entstehen mit der Geraden die Schnittpunkte B1 und B2. 

...... Zeichnet man durch Punkt A alle möglichen Geraden und ermittelt wie soeben beschrieben Punktepaare, so bilden sie die gerade Strophoide. 
Beweis
...... >Nach dem Satz des Pythagoras gilt SB²=x²+(y-s)² oder wegen SB=NS gilt (I) s²=x²+(y-s)².
>Die Gerade AB hat die Gleichung y=sx+s. Dann ist (II) s=y/(x+1).

(II) in (I) eingesetzt ergibt y²/(x+1)²=x²+[(y-y/(x+1)]² oder y²=x²(x+1)²+x²y² oder y²-x²y²=x²(x+1)² oder y²(1-x²)=x²(x+1)² oder y²(1-x)=x²(1+x) wzbw.

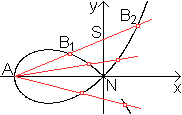
Strophoide und Kreisinversion     top
Die Inversion am Kreis ist eine Abbildung der ebenen Geometrie, bei der das Innere und das Äußere eines gegebenen Kreises miteinander vertauscht werden, und zwar nach Maßgabe von r1(t)*r2(t)=r². 
Unter bestimmten Voraussetzungen geht eine Strophoide in sich selbst und eine Hyperbel in eine Strophoide über.


Die Strophoide geht in sich selbst über.
......
 In dieser Lage hat die Strophoide die Polargleichung r(t)=[1-sin(t)]/cos(t).
Spiegelt man am Einheitskreis, so müsste [r(t)]²=1 gelten.
Es ist [r(t)]²=[1-sin(t)]²/cos²(t).
Setzt man zum Beispiel t=pi/4, so ist [r(pi/4)]²=[1-sin(pi/4)]²/cos²(pi/4)=6-2sqrt(2)
Also gilt [r(t)]²=1 nicht allgemein.

Dieses Dilemma löst sich auf, wenn man weiß, dass auch r2(t)=[1+sin(t)]/cos(t) die Strophoide beschreibt, allerdings wird sie dann in Gegenrichtung durchlaufen.
Dann gilt r(t)*r2(t)={[1-sin(t)]/cos(t)}*{[1+sin(t)]/cos(t)}=[1-sin²(t)]/cos²(t)=1, wzbw.
Mehr auf der Webseite http://haftendorn.uni-lueneburg.de (URL unten)
Eine Hyperbel geht in eine Strophoide über.
......
Hyperbel: x²-y²-1=0
Strophoide:   y²(3-x)-(x-1)²(1+x)=0
Kreis: (x-1)²+y²-1=0
 

Entdeckt auf der Seite http://xahlee.org/SpecialPlaneCurves_dir/Hyperbola_dir/hyperbola.html

Weitere Kurven mit Schleifen top
Es gibt viele andere Kurven in Schleifenform.
...... Das ist eine Schleifenkurve mit der einfachen Gleichung y²=-x²(x-1).

An den Bezeichnungen der folgenden Schleifenkurven sieht man, dass sie in der Geschichte der Mathematik eine Rolle gespielt haben. Ich habe die Namen mit einem Link auf die entsprechende Seite von MacTutor History of Mathematics archive verknüpft. So kann man sich einen ersten Überblick verschaffen. 
 
 
Tschirnhausen-Kubik

27ay²=x²(9a-x) mit a=-1
Kartesisches Blatt

x³+y³-3axy=0 mit a=1
Konchoide

 (x-a)²(x²+y²)-b²x²=0 mit a=1 und b=2.
Konchoide von de Sluze

(x-1)(x²+y²)-a²x²=0 mit a=1
Trisectrix des Maclaurin

2x(x²+y²)+4(3x²-y²)
Szegö-Kurve

x²+y²=e2x-2

Kuriositäten

Dreistrahlige Figuren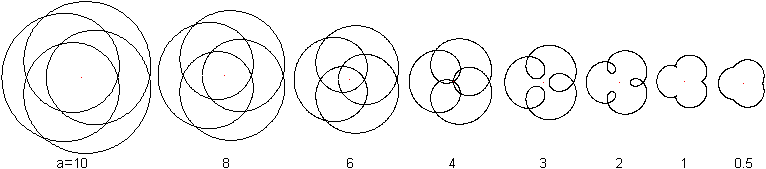

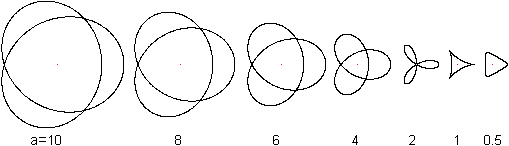Vierstrahlige Figuren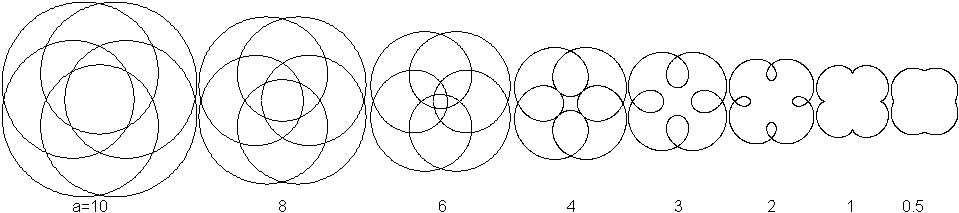

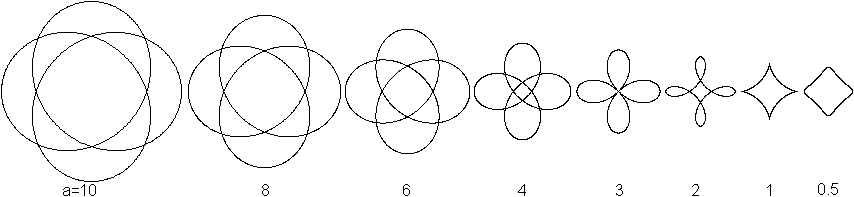Strophoide im Internet     top

Deutsch

Eckart Schmidt
Strophoiden  (.pdf-Datei)

Wikipedia
Strophoide, Inversion (Geometrie)


Englisch

Eric W. Weisstein  (MathWorld) 
Right Strophoid, Strophoid

MacTutor History of Mathematics archive  [University of St Andrews, Scotland]
Right Strophoid

Wikipedia
Strophoid, Inversive geometry


Französisch

Robert FERRÉOL
STROPHOÏDE, STROPHOÏDE DROITE

Referenzen    top
(1) I.N.Bronstedt, K.A.Semendjajew: Taschenbuch der Mathematik, Leipzig 1987
(2) M.J.Wygodski: Höhere Mathematik griffbereit, Braunschweig 1977 [ISBN 3 528 18309 8] Seite 723ff.

Feedback: Emailadresse auf meiner Hauptseite

URL meiner Homepage:
https://www.mathematische-basteleien.de/

©  2009 Jürgen Köller

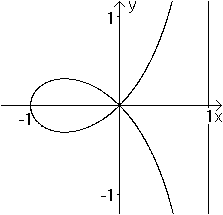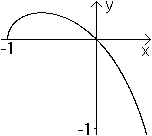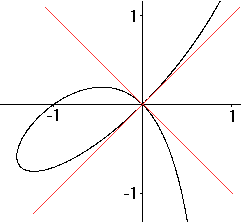
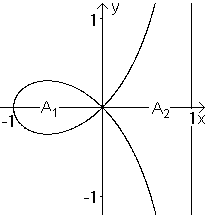
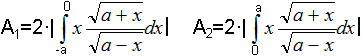
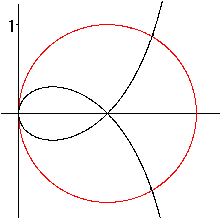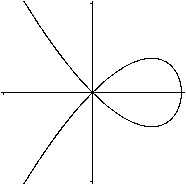top