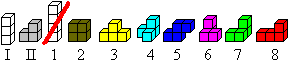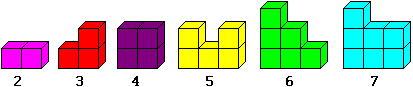|
What is a Soma Cube?
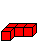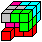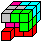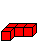
The seven pieces of cubes are named
Soma cubes. Altogether you have 1x3 + 6x4 = 27 separate smallcubes.
Main Problem top
... ... |
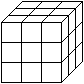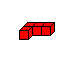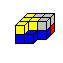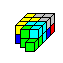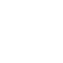
The main problem of the Soma "research"
is to assemble the seven Soma pieces or 27 cubes to make a 3x3x3 cube.
The chance of solving this three-dimensional
puzzle is good, because there are 240 possibilities to put
the cube together, not counting symmetries.
If you try to solve the puzzle for
the first time, you need approximately 15 min. You have a better chance
if you start with the three-dimensional pieces 5,6,7. |
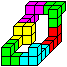
Three solutions
1
... ...
|
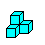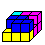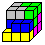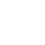2
 ...
|
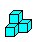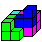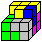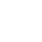3
 ...
|
Solution 1 was my first solution, which I kept in my
mind.
Solution 2 is easy to remember: You start with the three
3D pieces 5,6, and 7. Piece 4 follows.
Solution 3 is one of the few solutions without piece
7 forming a corner. |
All 240 solutions
Loesung Nr: 1
000 100 000 011 000
000 000
000 000 000 001 110
000 000
000 000 011 000 100
000 000
000 100 000 001 000
010 000
000 110 001 000 000
000 000
000 000 001 000 000
000 110
000 000 000 000 000
111 000
111 000 000 000 000
000 000
100 000 000 000 000
000 011
 |
... ... |
Jochen Wermuth makes available all 240 solutions found
by a program in C++.
He is using the notation on the left.
The pattern has seven rows. The whole cube and the position
of a soma cube is given in a row.
The three blocks in the lines are assigned to the three
layers on top, centre and bottom. |
I offer all
240 solutions for downloading, likewise the source
code in C++ with the author's agreement.
Positions
of the Soma Pieces 3 and 2 top
Piece 2 and 3 contain a 1x1x3 bar.
The shapes of the Soma cubes result in the following statements.
Piece 2 forms 0,1 or 2 corners.
Piece 3 forms either 0 or 2 corners.
Now there are two possibilities:
(1) Piece 3 forms no corners. The other six pieces form
at most 2+5 corners. This case is not possible, because you don't have
eight corners.
(2) Piece 3 forms two corners. The other 6 pieces form
6 corners. Therefore piece 2 must form at least one corner.
Results:
........ ..
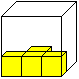Piece 3 forms two corners. |
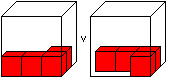
Soma piece 2 must always form a corner and must not lie
in the middle. |
This can be the first steps to prove that there are 240 solution.
Figures
of Soma Cubes top
It is interesting to look for new
27-cube-shapes. This is one example, a "car".
More well known figures are sofa,
bed, bathtub, gate, gravestone, and tower.
There are innumerable figures of
Soma cubes. This is proved by the following thoughts about designing new
ones.
... ... |
All Soma cubes have 27 cubes. If you give a mat of
5x4 = 20 cubes, there are [20 above 7] = 20!/13!/7! = 77520 places for
the remaining seven cubes, so 77520 figures. There is an example on the
left. |
... ... |
If you form a bar with five cubes, there are two left.
So you get [15 above 2] =15!/13!/2! = 105 figures. There is an example
on the left. If you demand symmetry, you only get 18 cube figures. You
can see them as top view on the right and in perspective below. |
... ... |
Two figures are insoluble.
Magnification Problem
top
Can you imitate a somacube with magnification? It is
a productive problem with pentominos and tetracubes, but not with Soma
cubes. Only the cube with three cubes is possible. You need the rest of
the Soma cubes to build it with double magnification.
Making
of Soma Cubes top
If you want to play with Soma cubes
you have to construct them by hand.
The simpliest way is to buy a length of wood which is
square in cross-section, cut it into cubes and glue the cubes together.
Another method is glueing dice.
The best idea is to use a two component glue, because it needs time to
harden. Then you can form the Soma pieces without having to hurry.
A cheap but difficult method is constructing them from
a sheet of paper. You have to design the base of every Soma cube and fold
it.
You can buy Soma cubes.
Parker Brothers sold the Soma cubes in 1969. Maybe they
protected the name "Soma cube" by copyright.
In Germany you can buy them on Christmas fairs, mostly
without a name or with other names like Ostfriesenwürfel ;-). Another
version is Babylon. This is the "Rehmsche Spielsatz".
In the United States there is a game using Soma cubes,
called Block by Block, which I bought in Las Vegas in 1996.
Three variants
1st Variant: Soma schräg
(Soma
crooked) top
There is a curiosity: You don't use a cube as the basic
piece, but a parallelepiped. This is a figure bordered by parallelograms.
In this case it is a rhombus with an 50° angle.
You should think you can simply apply the solutions of the
3x3x3 cube problem to this figure. You seldom succeed.
... ... |
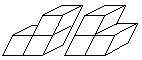If you add three or four parallelepipeds, you get two
possibilities of each Soma cube form. I only found one solution. |
(Soma schräg, HOLZINSEL 56290 Beltheim, Art.-Nr.
019/1)
2nd Variant:
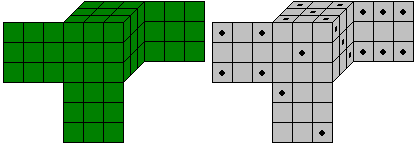
Chequered Pattern top
You can produce this Soma puzzle, if you build a cube with
method 2 and colour the cubes black and white alternately. This pattern
is transfered to the Soma pieces.
The problem is to form again a 3x3x3 cube of all pieces.
3rd Variant:
Coloured Cube
top
... ...
|
You can design new Soma puzzles, if you build a 3x3x3
cube and colour the surface all in one colour. You can also make a pattern
(Example: die). The Soma pieces will adopt these changings, too.
If you like you can transfer these changings to inner
squares in order to make the puzzle more difficult. |
The problem is to form again a 3x3x3 cube of all pieces.
History top
There are several forerunners of Soma Cubes.
In 1936 the Dane Piet Hein took seven polycubes, so that
they formed a 3x3x3-cube.
There are ten pieces with 2,3, and 4 cubes. He chose
the polycubes, which don't form a cuboid.
Maybe he obtained the name from the book "Brave New World"
by Aldous Huxley. Soma was the name of an addictive drug used in the fictional
state in Huxley's book which is set in the year 2600.
Piet Hein (1905-1996) was a poet and scientist with wide
ranging interests.
J.H. Conway and M.J.T. Guy worked out in 1961 that there
are 240 possible ways to form a 3x3x3-cube.
Computers confirmed this result later.
The Soma cubes became famous by its publication in the
magazine Scientific American (1958). In Germany the magazine
Bild
der Wissenschaften
circulated this puzzle (1967).
Similar Cube problems
top
Tetracubes
Theodore Katsani suggested a game with all polycubes
of four cubes in the 1950s.
It is impossible to build a 3x3x3 cube, but 8*4=32
leads to cuboids 2x4x4 or 2x2x8 (4). You find more on my page tetracube.
Rehm's Cube Set
There is the problem: Which polycubes with 3 or 4 cubes
form a 3x3x3 cube?
|
There are 2 tricubes and 8 tetracubes.
...
The numbers are used in book 5. |
There are 14 possibilities for a 3x3x3 cube because of
27=3+6*4.
I345678 (138)
|
I245678 (000)
|
I235678 (031)
|
I234678 (099)
|
I234578 (245)
|
I234568 (245)
|
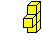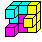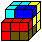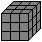
I234567 (027)
|
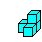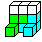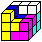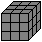
II345678 (240)
Somawürfel
|
II245678 (047)
|
II235678 (261)
|
II234678 (221)
|
II234578 (337)
|
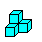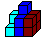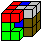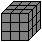
II234568 (337)
|
II234567 (039)
|
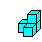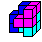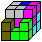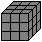
All
sets except the combination II2..45678
(3 is missing) leads to a cube (5).
The numbers inside the brackets
is the number of solutions (Torsten Sillke, Rehm's 3-Cubes, URL
below).
Hollow Cube
... ...
|
You can build a hollow cube from the tricubes I and II
and the tetracubes 3,4,6,7 and 8.
There is 2*3+5*4=26 |
You can ask for more solutions with other tetracubes of Rehm's
cube set and for the number of solutions.
(This idea had Volker Latussek from Würzburg.)
More 3x3x3-Puzzles
top
All soma cubes together contain 27 cubes. The distribution
is 27=3+4+4+4+4+4+4.
You can imagine that there are more sums between 27=1+1+...+1
and 27=9+9+9, which are suitable for puzzles.
I introduce some puzzles in this chapter, which I found
more at random.
Diabolical
Cube - Hoffmann (27=2+3+4+5+6+7)
... |
some solvable symmetric figures |
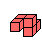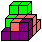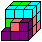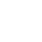
Mikusinski's
Cube (27=4+4+4+5+5+5)
... |
There are two solutions only. |
|
... |
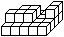I only found a 4x5 mat with 7 cubes on top, which is
worth to show, after playing around. |
Der
vertrackte Würfel- The tricky cube (27=4+4+4+5+5+5),
"Toys pure", Art.-Nr.:HS 630
... |
|
... |
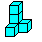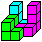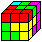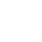
You can form a closed ring with all pieces. |
Loops
cube (27=4+4+4+5+5+5), designed and made by René Dawir
... |
Order in the solution: 564321 |
|
Soma Cube on
the Internet
top
German
http://www.zahlenjagd.at/
Würfelpuzzles
Matroid Matheplanet
Der
Soma Würfel
Thimo Rosenkranz
Soma-Figuren
Wikipedia
Somawürfel
English
Christian Eggermont
The
Soma Cube ("Go to the puzzles!")
Ed Vogel
A very large Soma puzzle
at the Minnesota State Fair 2006 |
|
Eric W. Weisstein, (MathWorld)
Soma
Cube
pelikanpuzzles.eu
SHRINKING
SOMA (more at Youtube)
Stewart T. Coffin
The
Puzzling World of Polyhedral Dissections
Thorleif Bungård
Thorleif's
SOMA page
Torsten Sillke
cube-secrets,
Rehm's
3-Cubes (1980)
Wikipedia
Soma
cube, Bedlam cube,
Conway
puzzle
Youtube
SOMA
CUBE puzzle solution, Puzzle
Cube Solution, How
to solve the Bedlam Cube Retro,
SOMA
CUBE ANIMATION (12 figures, 3D puzzle solution)
References top
(1) "Bild der Wissenschaft" November 1967
(2) Pieter van Delft /Jack Botermans: Denkspiele der
Welt, München 1980 (1998 neu aufgelegt) [ISBN 3-685-1998)
(3) Martin Gardner: Bacons Geheimnis, Frankfurt am Main,
1986 [ISBN 3-8105-0800-4]
Fast 30 Jahre nach Erscheinen einer Kolumne in der
Septemberausgabe 1958 von <Scientific American> zieht der Autor eine
Bilanz der "Somaforschung".
(4) R.Thiele, K.Haase: Der verzauberte Raum, Leipzig,
1991 [ISBN3-332-00480-8]
(5) R.Thiele, K.Haase: Teufelsspiele, Leipzig, 1991 [ISBN
3-332-00116-7]
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |
