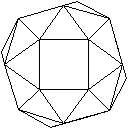
|
Was ist der abgeschrägte Würfel?
.. ....
|
Der abgeschrägte Würfel ist ein Körper,
der von 6 Quadraten und 32 gleichseitigen Dreiecken gebildet wird.
Der Körper heißt auch abgeschrägtes Hexaeder,
schräger Würfel oder Cubus simus. |
Neben den 6+32=38 Seitenflächen
hat der abgeschrägte Würfel 60 Kanten
und 24 Eckpunkte.
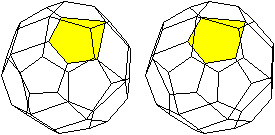
Die beiden folgenden, nebeneinander
liegenden Bilder ermöglichen mit dem "Stereoblick" eine dreidimensionale
Ansicht.
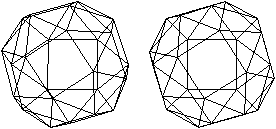
durchsichtig
|
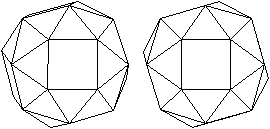
undurchsichtig
|
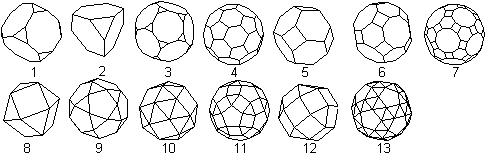Da beim abgeschrägten Würfel (10) an jeder Ecke
regelmäßige Vielecke in gleicher Weise aufeinandertreffen, gehört
es zu den 13
archimedischen Körpern.
Entstehung top
Der Körper entsteht aus einem Würfel, indem
man seine Seitenflächen (die Quadrate) dreht und gleichzeitig verkleinert.
Man verbindet dabei jeden Eckpunkt der Quadrate mit drei anderen Eckpunkten.
Es entstehen so zwischen den Quadraten Dreiecke. Man dreht und verkleinert
bis zu einem Drehwinkel, bei dem die Dreiecke gleichseitig sind.
Die folgende Bilderreihe zeigt diesen Vorgang an einer
Seitenfläche.
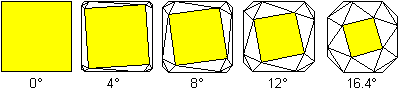
In der Zeichnung erkennt man bei 0° das Quadrat des
Ausgangswürfels. Nach einer Drehung von etwa 16,4° und gleichzeitiger
Schrumpfung ist der abgeschrägte Würfel entstanden.
... ... |
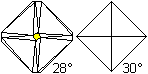Dreht und verkleinert man weiter, so zieht sich bei 30°
das Quadrat zu einem Punkt zusammen. Es ist ein Oktaeder entstanden.
Der abgeschrägte Würfel kann danach auch durch
eine Drehung von 30° auf 16,4° aus einem Oktaeder entstehen. |
Das Quadrat wird entgegen
dem Uhrzeigersinn gedreht.
Am Ende wird noch ein Spiegelkörper erwähnt,
bei dem das Quadrat im Uhrzeigersinn gedreht wird.
Die hier beschriebenen Vorgänge
zeigen zwei Applets von Geneviève Tulloue (URL
unten).
Beschreibungen top
Umgebungen
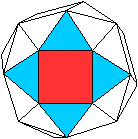
Jedes Quadrat ist
von 4 Dreiecken umgeben.
|
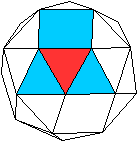
(I) Ein Dreieck ist von 2 Dreiecken
und einem Quadrat umgeben.
|
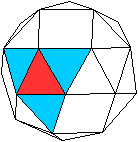
Oder: (II) Ein Dreieck ist
von 3 Dreiecken umgeben.
|
Besondere
Ansichten
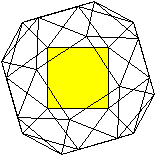
Ein Quadrat liegt vorne.
|
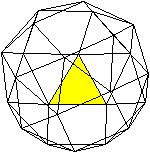
(I) Ein Dreieck liegt vorne.
|
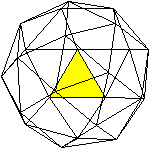
(II) Ein Dreieck liegt vorne.
|
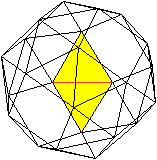
Die gemeinsame Seite
zweier Dreiecke liegt vorne.
|
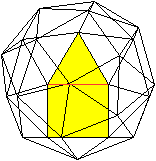
Die gemeinsame Seite von
Dreieck/Quadrat liegt vorne.
|
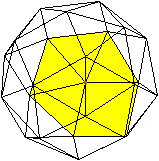
Ein Eckpunkt liegt vorne.
|
Die drei letzten Bilder sind Schätzungen.
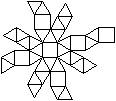
Netz und Schlegel-Diagramm
Diagonalen
12 Flächendiagonalen
... .... |
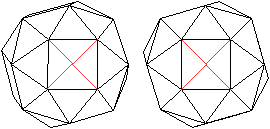Die Diagonalen der Quadrate sind die Flächendiagonalen
des abgeschrägten Würfels.
Das Quadrat hat 2 Diagonalen.
Das führt zu insgesamt 6*2=12 Flächendiagonalen. |
204
Raumdiagonalen
... ... |
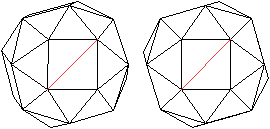Von jedem der 24 Eckpunkte gehen Verbindungslinien zu
den anderen Eckpunkten aus. Das sind eine Flächendiagonale und 5 Kanten,
wie die Zeichnung zeigt. In 24-6=18 Punkten enden dann Raumdiagonalen.
Das führt zu insgesamt (1/2)*24*17=204 Raumdiagonalen des abgeschrägten
Würfels. |
Bilanz
Auf meiner Seite Dreieckszahlen
steht: "Verbindet man n Punkte mit allen möglichen geraden Linien,
so ergeben sich 1+2+3+...+(n-1)=(1/2)(n-1)n Strecken."
Für den abgeschrägten Würfel bedeutet
das, dass es (1/2)*24*23=276 Verbindungslinien gibt.
Das sind die 60 Kanten, 12 Flächendiagonalen und
204 Raumdiagonalen.
Größen top
Vorweg: Tribonacci-Konstante
Die Formeln des abgeschrägten Würfels sind
eng verknüpft mit der Tribonacci-Konstanten t, der reellen Lösung
der Gleichung x³ - x² - x - 1 = 0.
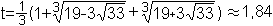
Der Name der Konstanten t erschließt sich über
die "Tribonacci-Folge", einer Varianten der bekannten Fibonacci-Folge.
Das Bildungsgesetz der Folge ist T1=1, T2=1,
T3=2 mit der Rekursionsformel Tn=Tn-1+Tn-2+Tn-3
(n>3).
Das führt konkret zur Folge 1, 1, 2, 4, 7, 13, 24,
44, 81, 149, ... (Sloane's A000073).
Der Quotient aufeinander folgender Glieder nähert
sich zunehmend der Tribonacci-Konstanten t.
Formeln
Der abgeschrägte Würfel sei durch die Kantenlänge
a
gegeben.
Daraus lassen sich die Größen Volumen V,
Oberfläche O, Radius
R der Umkugel, Abstand der Dreiecke
d3
=2r3 und Abstand der Quadrate
d4 =2r4
berechnen.
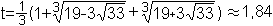
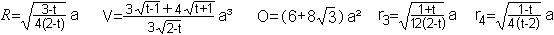
Quelle: MathWorld
Zur
Herleitung der Formeln
Die Oberfläche setzt sich aus 32 Dreiecken und 6
Vierecken zusammen.
O=32*A3+6*A4=32[(1/4)sqrt(3)]+6a²=8sqrt(3)a²+6a²=[6+8sqrt(3)]a²,
wzbw.
Weitere Herleitungen dürften
schwierig sein.
Weitere Körper top
Pentagonikositetraeder
... ... |
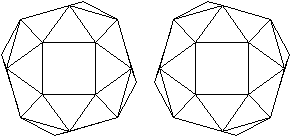
Verbindet man die Mittelpunkte benachbarter Seitenflächen
des abgeschrägten Würfels, so entsteht der duale Körper,
das Pentagonikositetraeder. |
Spiegelkörper
Oben wurde schon erwähnt, dass der abgeschrägte
Würfel einen Spiegelkörper hat. Man erhält ihn, wenn
man den abgeschrägten Würfel an einer passenden Ebene spiegelt.
Das ist kein Stereobild.
Es gibt nur noch einen zweiten archimedischen Körper,
der einen Spiegelkörper hat. Das ist das abgeschrägte
Dodekaeder.
Der
abgeschrägte Würfel im Internet top
Deutsch
H. B. Meyer (Polyeder aus Flechtstreifen)
Abgeschrägter
Würfel
Wikipedia
Abgeschrägtes
Hexaeder, Archimedischer
Körper, Catalanischer
Körper, Pentagonikositetraeder
Englisch
Eric W. Weisstein
Archimedean
Solid, SnubCube,
Pentagonal
Icositetrahedron, Tribonacci
Constant, Tribonacci
Number
Geneviève Tulloue ( Figures Animées pour
la Physique )
The
Snub Cube (1) (Applet), The
Snub Cube (2) (Applet)
Gijs Korthals Altes (Paper Models of Polyhedra)
Snub
cube
H. B. Meyer (Polyeder aus Flechtstreifen)
Snub
Cube
Poly
A program
for downloading (Poly is a shareware program for exploring and constructing
polyhedra)
Die meisten Zeichnungen auf dieser Seite entstanden
mit Hilfe dieses Programms.
Wikipedia
Snub
cube, Archimedean
solid, Catalan
solid, Pentagonal
icositetrahedron
Referenzen top
(1) H.Martyn Cundy and A.P.Rollett: Mathematical Models,
Oxford 1961 (Seite 107)
Feedback: Emailadresse
auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2008 Jürgen Köller
top |
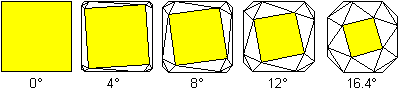
