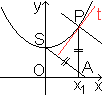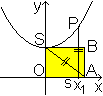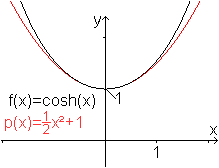|
Was ist eine Kettenlinie?
...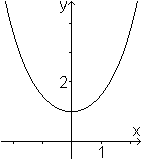 ... ... |
Die Kettenlinie (Katenoide) ist der Graph der Funktion
f(x)=cosh(x) oder f(x)=(1/2)(ex+e-x).
Man spricht cosh als Cosinus Hyperbolicus.
Der Name Kettenlinie rührt daher, dass eine
Kette diese Form annimmt, wenn man sie an zwei Punkten aufhängt. Cosh
wird
weiter unten erklärt. |
 ... ... |
Graphische Addition
top
...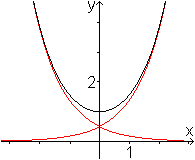 ... ... |
Zeichnet man die Graphen der Exponentialfunktionen f1(x)=(1/2)ex
und f2(x)=(1/2)e-x und addiert die y-Werte punktweise,
so erhält man den Graphen der Funktion f(x)=f1(x)+f2(x)=cosh(x).
Das ist ein einfacher Weg, um sich ein Bild von der Funktion
zu machen. |
Zur Herleitung
der Formel top
Über eine Kräftebetrachtung
leitet
man die Differentialgleichung ay''=sqrt(1+y'²) her,
wie z.B. auf der Webseite von René Grothmann (URL unten)
dargestellt.
Sie ist eine Bestimmungsgleichung für die gesuchte
Funktionsgleichung der Kettenlinie.
Sie wird gelöst von y=a cosh(x/a+c1)+c2,
im wesentlichen von y=a cosh(x/a), wie ein Einsetzen in die Differentialgleichung
zeigt.
Für y=a cosh(x/a) oder y=(a/2)(ex/a+e-x/a)
gilt y'=(1/2)(ex/a-e-x/a) und y''=[1/(2a)](ex/a+e-x/a).
Dann ist 1+y'²=1+ (1/2)2(ex/a-e-x/a)2=1+
(1/4)[(ex/a))²-2(ex/a)e-x/a))+(e-x/a))²]=1+(1/4)(ex/a))²-(1/2)+(1/4)(e-x/a))²
=(1/4)[(ex/a))²+2(ex/a)e-x/a))+(e-x/a))²]=(1/4)(ex/a+e-x/a)²
und weiter sqrt(1+y'²)=(1/2)(ex/a+e-x/a)=a[1/(2a)](ex/a+e-x/a)=ay'',
wzbw.
(Buch 2, Seite 538).
Ergebnis:
Die Funktionenschar fa(x)=a*cosh(x/a) oder
fa(x)=(1/2)a(ex/a+e-x/a) beschreibt die
Kettenlinie.
Dabei ist a ein Parameter ungleich Null.
Die Ausgangsfunktion f(x)=(1/2)(ex+e-x)
ist unter den Lösungen. Man setze a=1.
Diese Herleitung hält sich an Buch (1), Seite 520ff.
Graph von fa(x)=a*cosh(x/a)
...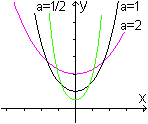 ... ... |
Der Parameter a beschreibt die "Öffnung" der Kettenlinie
und gibt die Entfernung des Scheitelpunktes vom Nullpunkt des Koordinatensystems
an. |
Ähnlichkeit
der Kettenlinien
top
So wie z.B. die Kreise und die Parabeln sind die Kettenlinien
ähnlich.
Zwei Figuren sind ähnlich, wenn sie durch eine einfache
Verkleinerung oder Vergrößerung ineinander übergeführt
werden können. Das erreicht man durch eine Maßstabänderung.
Man wählt x=aX und y=aY.
Dann wird y=(1/2)a[e(1/a)x+e-(1/a)x]
zu aY=(1/2)a[e(1/a)aX+e-(1/a)aX] oder Y=(1/2)[eX+e-X].
Aus jeder Kettenlinie mit fa(x)=a*cosh(x/a)
wird also eine Normal-Kettenlinie.
Ableitung top
Wegen der Grundformel (ex)'=ex ist
cosh(x) leicht zu differenzieren und zu integrieren.
...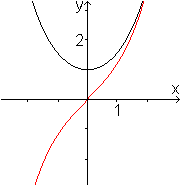 ... ... |
Es ist f(x)=cosh(x)=(1/2)(ex+e-x)=(1/2)ex+(1/2)e-x.
Nach Ableitungsregeln ist dann f '(x) = (1/2)ex-(1/2)e-x
=
(1/2)(ex-e-x)
Man fasst den Term (1/2)(ex-e-x)
als Funktionsterm einer neuen Funktion auf,
dem Sinus Hyperbolicus: g(x)=sinh(x). Die rote Kurve
ist ihr Graph. |
Leitet man f ' noch einmal ab [f ''(x) = (1/2)(ex+e-x)],
so ergibt sich wieder f(x)=cosh(x).
Die Stammfunktion ist F(x)=sinh(x).
Drei
Berechnungen - ein Ergebnis top
1 Steigung in Punkt P
...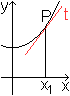 ... ... |
Oben wurde schon gezeigt, dass die Ableitung von f(x)=cosh(x)
gleich f '(x)=sinh(x) ist.
Die Steigung in Punkt P[x1)|cosh(x1)]
ist also sinh(x1). |
2 Länge
s des Kurvenstücks SP
...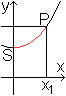 |
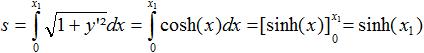 |
3 Flächeninhalt
unter der Kurve
...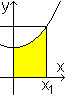 |
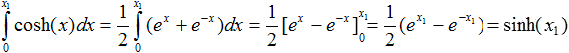 |
Veranschaulichungen
...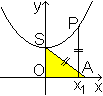 ... ... |
Es ist y=(1/2)(ex+e-x).
Dann ist y²-1=cosh²(x)-1=(1/4)(ex+e-x)2-1=(1/4)e2x+1/2+(1/4)e-2x)-1=(1/4)(ex-e-x)²=s²
Die Gleichung y²-1²=s² wird links durch
ein Dreieck dargestellt, indem man die Strecke des y-Wertes in den ersten
Quadranten einpasst. |
Ausgehend vom Dreieck kann
man sich Folgendes überlegen.
...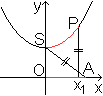
SP=OA=s
|
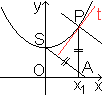
SA steht senkrecht zur Tangente t
|
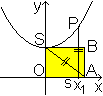
Das Rechteck OABS ist flächengleich der Fläche
unter der Kurve SP
|
Quelle: Buch (1), Seite 526.
Da wird auch gezeigt, dass die Veranschaulichungen für
alle Funktionen der Schar fa(x)=a*cosh(x/a) gelten.
e^(ix)=cos x+ i sin x. Darum muss es folgendermaßen weitergehen:
e^(ix)+e^(-ix)= cos x+ i sin x + cos x -i sin x= 2 cos x
Also cos x= cosh (ix). mit dem Argument ix für x folgt cos(ix)=cosh(i^2x)=cosh(-x)=cosh(x),
da letztere Fkt gerade ist.
Beziehung
zu den Kreisfunktionen
top
Es stellt sich die Frage, warum die Kettenlinie mit cosh
und die Ableitung mit sinh bezeichnet werden.
Da muss man den Bereich der reellen Zahlen verlassen und
zu komplexen Zahlen übergehen.
Die eulersche Formeln eix=cos(x)+i*sin(x)
bzw. e-ix=cos(x)-i*sin(x) mit i=sqrt(-1) geben eine Erklärung.
Es gilt eix+e-ix=[cos(x)+i*sin(x)]+[cos(-x)-i*sin(-x)]=
2*cos(x).
Dann ist cos(x) = (1/2)(eix+e-ix)
oder cos(x) = cosh(ix).
Weiter ist cos(ix) = cosh(i²x) oder cos(ix) = cosh(-x)
oder cos(ix) = cosh(x) oder cosh(x) = cos(ix).
Entsprechend leitet man sinh(x)=-i*sin(ix) her.
Mehr findet man zum Beispiel
auf der Wikipedia-Seite
Kreis- und Hyperbelfunktionen (URL unten).
Parabel und Kettenlinie
top
Die Kettenlinie ist keine Parabel, hat aber eine Parabelform.
Es stellt sich die Frage, welche Parabel der Kettenlinie
nahe kommt.
Dazu zieht man die Reihenentwicklung von cosh(x) heran.
ex= 1 + x/(1!) + x2/(2!) + x3/(3!)
+ x4/(4!) + ...
e-x= 1 - x/(1!) + x2/(2!) - x3/(3!)
+ x4/(4!) - ...
=> (1/2)(ex+e-x) = 1+ x2/(2!)
+ x4/(4!) + x6/(6!) + ...
Wenn man die Reihe nach dem zweiten Glied abbricht, erhält
man die Parabelgleichung p(x) = (1/2)x²+1.
...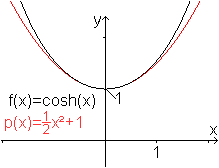 |
Bestätigung:
p(x) beschreibt die Kettenlinie in der Nähe x=0 recht
genau. |
Eine bessere Annäherung
erreicht man mit der biquadratischen Funktion mit b(x)=(1/24)x4+(1/2)x²+1.
Kettenlinie im
Internet top
Deutsch
Arndt Brünner
Die
Kettenlinie (mit Applet)
René Grothmann (Universität Eichstätt)
Die
Kettenlinie
Wikipedia
Katenoide,
Sinus
Hyperbolicus und Kosinus Hyperbolicus, Tangens
Hyperbolicus und Kotangens Hyperbolicus,
Sekans
Hyperbolicus und Kosekans Hyperbolicus, Areasinus
Hyperbolicus und Areakosinus Hyperbolicus,
Kreis-
und Hyperbelfunktionen, Eulersche
Identität, Gateway
Arch
Englisch
Eric W. Weisstein
Catenary,
Catenoid,
Roulette
jan wassenaar (2dcurves)
hyperbolic
cosine
Jonathan Lansey
Catenary
Demonstration Experiment
Paul Kunkel
Hanging
With Galileo
Robert Osserman
Mathematics
of the Gateway Arch
Wikipedia
Catenary,
Hyperbolic
function,
Inverse
hyperbolic function, List
of integrals of hyperbolic functions, Euler's
identity, Jefferson
National Expansion Memorial
Französisch
Robert FERRÉOL (mathcurve)
CHAÎNETTE
Referenzen top
(1) Georg Ulrich, Paul Hoffmann: Differential- und Integralrechnung
zum Selbstunterricht, Hollfeld [ISBN 3 8044 0575 4]
(2) Autorengemeinschaft: Analysis für Ingenieure,
Frankfurt/M Zürich 1966
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2009 Jürgen Köller
top |
 ...
... ...
... ...
... ...
...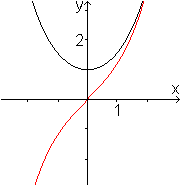 ...
... ...
...
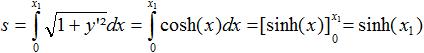

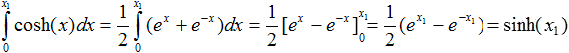
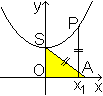 ...
...