Contents of this web page
|
What are Kolams, what are Sona?
Kolams are Indian floor paintings; sona (singular lusona)
are African sand paintings.
The only thing they have in common is that dot patterns
are given as a mnemonic and then lines are drawn around the dots so that
each dot is circled. The result is a great variety of attractive symmetrical
figures.
You can get an impression
of kolams and sona by watching the first two Youtube videos in the link
list below.
Kolams and sona are the subject
of ethnomathematics. There are links at the end of this web page.
Example of a kolam, example
of a lusona
Kolams top
Background
A kolam is a South Indian floor
painting.
In certain regions in South India,
women decorate the floors in front of houses with elaborate, rotationally
symmetrical figures. They draw dots
with rice flour as a guide and
then draw lines around the dots. To do this, they skillfully let powder
trickle between their index finger
and middle finger and portion it
out with their thumb.
The often complicated patterns
are passed on from generation to generation in a family. - They have a
religious background.
These kolams are more precisely
called stroke kolams on the English Wikipedia page, neli kolam, kambi kolam
or sikku kolam in Tamil.
In
other regions, point grids and lines are dispensed with. Instead, coloured
areas or carpets of flowers are laid out. Rice flour is replaced by stone
powder or chalk powder, often together with natural or synthetic colour
powders.
The pictures, which always have
rotational symmetry, are presented together with the stroke kolams at celebrations,
at festivals, in competitions and on the internet.
Simple
Example
...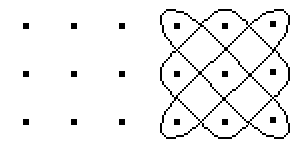 ... ... |
If you give nine points in square form, a kolam could
look like this. |
... ... ... |
Kolams are created by closed, overlapping lines.
In this case, the image is created from the three edge
curves of the yellow pieces. |
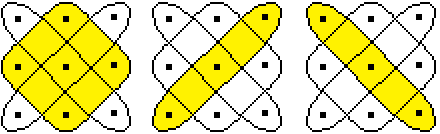
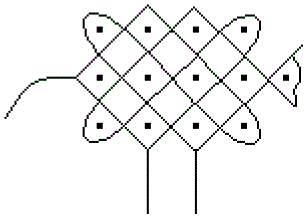
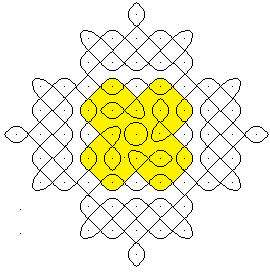
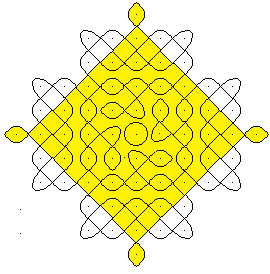
Example
of a Kolam
This kolam is created by
seven closed curves, marked by the lines in red (4x), green, blue and violet.
The structure of the kolam
is better recognized by yellow colorings.
- There are four outer figures and a central circle.
- In the center is a rounded cross.
- A square with tines surrounds the figure.
The kolam is created by drawing the closed lines.
Several closed lines, this is typical for kolams, although
they sometimes get by with one closed line.
Sona top
Background
Sona are traditional drawings of
some Bantu people like the Chokwe in an area of Angola and Zambia in southern
Africa.
Storytellers draw sona with their
finger in the smooth sand while telling a story. Without putting the finger
down, a closed line is drawn. The line leads around points of a predefined
pattern, crosses again and again and finally returns to the starting point.
The drawings illustrate the stories.
Simple
Example
The figure to a 4x3 grid is a lusona. It therefore consists
of a closed line without beginning and end. The figure is monolineal.
As the sona complement stories,
they often depict animals.
Antelope
... ... ... |
The compact lusona becomes an antelope...................................
Do you feel the irony in this picture? I do |
Leopard
|
The picture shows a leopard with extended paws, on the
left the little head, on the right the little tail.
More precisely: Two cubs are also visible in the drawing.
They are lying next to each other and opposite each other. |
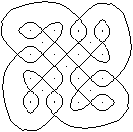
(1)
Three
Birds
... ... ... |
There are also sona in which images are repeated. They
are connected in such a way that a
closed line is maintained.
Here there are three birds, in my reference there are
ten (!).
(2) |
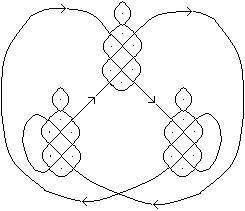
A Fable
... ... ... |
This lusona is also drawn with a closed line.
Four almost identical figures are linked together.
The abstract figure comes alive when you know the fable
that is told while drawing. |
...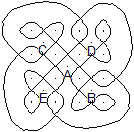 ... ... |
"The following sand drawing illustrates
a fable: Sambálu, the rabbit (positioned a point B), discovers a
salt mine (point A). Immediately, the lion (point C), the jaguar (point
D), and the hyena (point E) demand possession, asserting the rights of
the strong. The rabbit, affirming the inviolable rights of the weak, then
quickly makes a fence to isolate the mine from all usurpers.
Note that only from B can one go
to point A, without going beyond the line that represents the fence."
(3) |
Exceptionally, when the story
requires it, sona consists of several closed lines.
But on this page, for simplicity, a figure is called
a lusona when they arise from a closed line.
Some Mathematics top
Mirror Model
...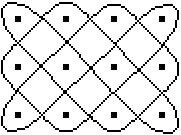 |
This lusona 4x3 is used to describe how the figure is
"mathematised" on the basis of a model conception. |
...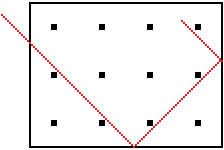 ... ... |
Place a rectangle around the 4x3 points and imagine that
the rectangle is mirrored on the inside. If a ray
of light is sent into the rectangle from the upper left, it is reflected
many times and describes a path as started on the left.
The ray drawn in is not allowed. The path is controlled
by grids.
|
... ... ... |
A grid is placed in the rectangle............................................................................................ |
...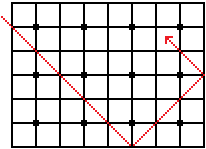 ... ... |
A ray of light is sent into the rectangle in such a way
that it makes its way exactly between the predefined points. |
...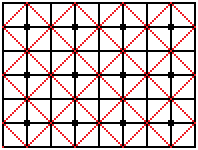 ... ... |
Finally, it returns to the starting point; it crosses
all the squares on diagonals.
What remains is a grid of squares standing on top. |
...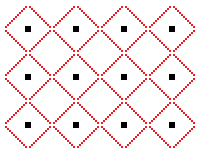 ... ... |
When you delete the black grid, then the red grid is
more clearly visible. ................................................. |
...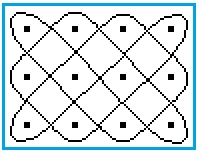 ... ... |
It is easy to recognise the 4*3-lusona above in the grid
of light rays.
The curves can be explained by the fact that the walls
of the rectangle act as mirrors. |
First
Rule
The question arises which rectangular figures m*n is
a lusona.
Here are four examples:
...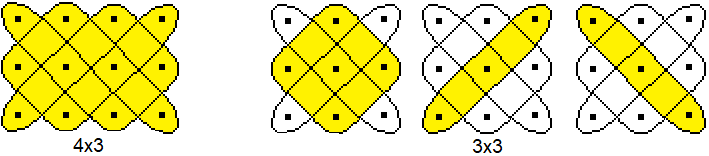
...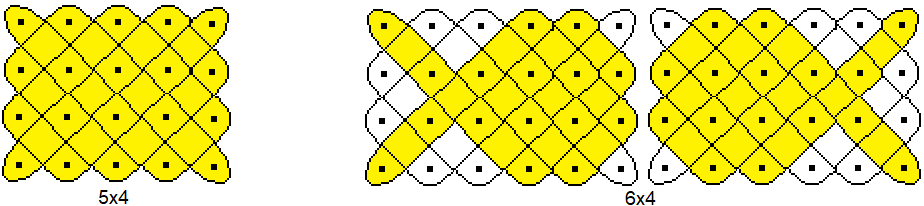
These four examples
illustrate the following first rule.
- A closed line only results if m and n have no
common divisor.
- If several closed lines are necessary to create
the figure, the number of curves is equal to the greatest common divisor.
The rectangles to the leopard
family have the data 10*3 and 2x3, their dimension numbers have no common
divisor.
... |
... ... ... |
The rectangles overlap in such a way that together they
are further created by a closed line. |
Inner
two-sided mirrors
... |
The compact lusona becomes more
interesting when you create patterns inside. |
...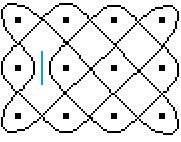 ... ... |
In the simplest case, you dissolve a crossed line and
replace the crossing with roundings.
This can be explained in the mirror model by placing a
two-sided mirror on a crossing. |
...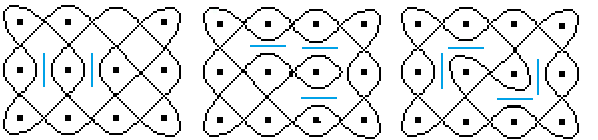 ... ... |
You can also put several mirrors inside.
(The figure on the right is a lusona.) |
With the insertion of a mirror,
the following figure can no longer created by a closed line.
... ... ... |
You need two closed lines to capture the figure. ..................................,,.,...................... |
... ... ... |
From this figure, by the way, you can create a lusona
again by resolving a crossing in which the two different lines meet. |
Second
rule
There is a simple rule for m*n-sona with one interior
mirror.
For this, a pattern of dark and light fields must be
introduced.
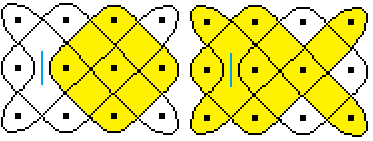
... ... ... |
You put the grid on the 4x3 lusona................................................................................. |
...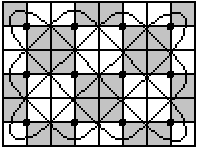 ... ... |
You follow a line and colour every second square grey.
For instance you start with a grey square at the upper
left corner. Then you go two squares to the right and one square down.
This square becomes grey again and so on. |
...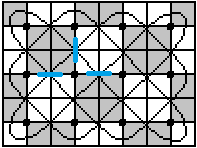 ... ... |
The second rule says that there can always be
a mirror where 2x2 squares meet.
These are the three mirrors and, for reasons of symmetry,
four more can be added.
This is confirmed by the study of the 42 figures in the
next chapter by the first three sona.
|
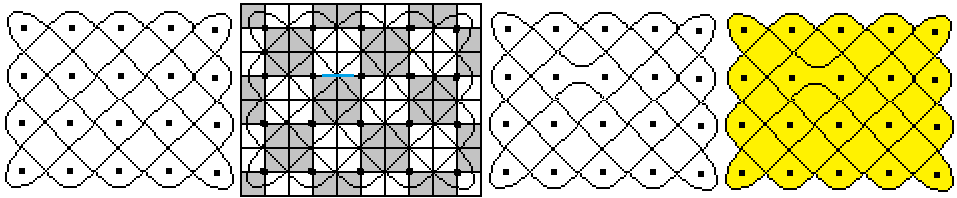
Another
example, the 5*4-Lusona
...
From
a Lusona to a Matrix
... ... ... |
...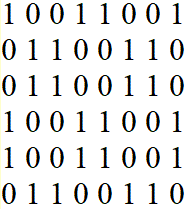 ... ... |
If you write number 1 in place of the dark fields and
a zero in place of the light fields, you get a matrix of zeros and ones.
It can be assigned to a 4x3 figure and uniquely identifies
it.
Conversely, you can design new patterns from 0 and 1 and
create at a new lusona. |
In
Search of Sona top
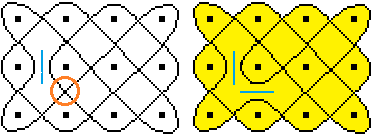
Question: Where must be placed mirrors inside the
4x3-lusona, so that the figure remains a lusona?
For this purpose, all possible positions of up to five
mirrors are played through..
...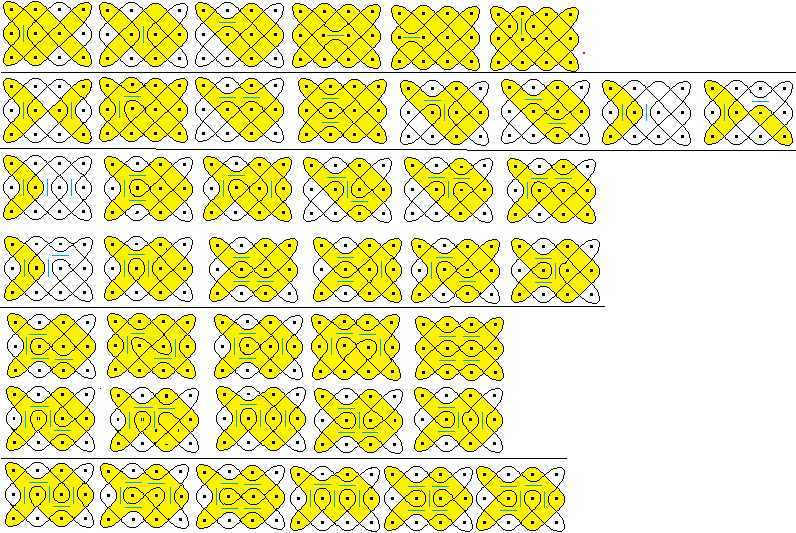
Result: Among the 42 figures examined, eight are a lusona.
Question: In the 3x3 kolam,
where must the double mirrors (blue) be inside and on the edge for the
figure to become a lusona?
...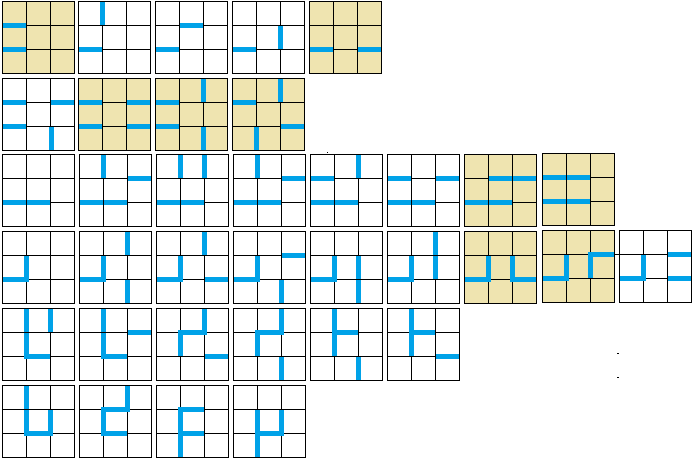
Result: There are 36 sonas, nine of which are symmetrical.
...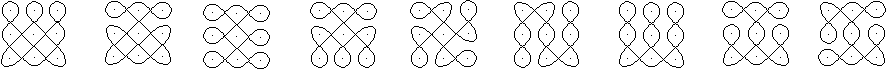
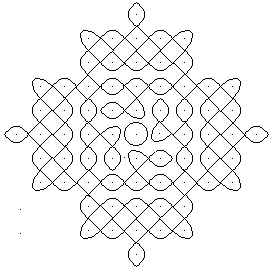
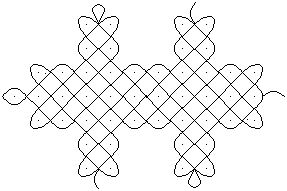
Question: How do you get
to the following kolam of five closed curves?
...
...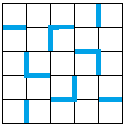 |
You draw a point-symmetrical figure with ballpoint pen
on checked paper in the hope that from it an
handsome kolam will be created. Draw it - as described
in the next chapter - with MS Paint or the online program. |
...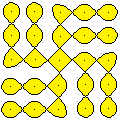 |
You also find sonas................................................................................................................................... |
Drawing
Exercises top
Five basic figures
Above it says that kolams are created
by drawing lines around points. If you have a field of 2x2 points, there
are many ways to circle dots.
...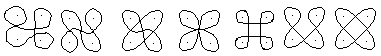
Kolams as a subject of mathematics
are composed of the following basic figures.
...
Thus the first four figures are
omitted. Only the next three figures are called kolams.
Strictly speaking, the fifth figure
must have a dot in the center.
Just
like the mandalas of Far Eastern cultures, the line kolams lend themselves
to their own activities.
Drawing with pen and paper
For example, if you have a 3x2
dot pattern and want to draw Kolams or even Sona, this is the best way
to go.
- Draw a 3x2 rectangle and
double mirrors at suitable places.
- Then you sketch the kolams.
It is difficult to do this, because you have to have the five basic figures
in your head.
- Then the sketches are transferred
into a final drawing. Use MS-Paint or the online program described below.
...
Drawing with MS-Paint
The drawings on this website were
created with the drawing program MS-Paint. It is available to anyone who
uses Windows on the Internet.
...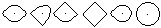 ... ... |
The figures are, as already indicated
above, composed of five building blocks together. A circle is added. |
I show two sequences
of pictures as a suggestion for your own activities.
...
You
can color the kolams.
...
Drawing
with a program
There is a program available on
the Internet that makes it easy to draw kolams.
You can get to the online program
by calling it in the link list below with the name Forkphorus.
The user interface is clear. On
the right is the tool, on the left is the drawing area for a maximum of
5x5 Kolams.
At the top the six basic figures
are available. You can bring a figure to the drawing area by tapping on
it and then on the target square. There are fields for turning and deleting
the figure. The field at the bottom right deletes the drawing. The field
at the bottom left has no effect on me.
The
program helped to find the sona among the 3x3 kolams in the previous chapter.
If you specify the compact 3x3 figure, you can "create" kolams by turning
basic figures. You can recognizes the position of the double mirrors as
gaps and can make out sona, even if the shapes are not correct.
Suggestion
Perhaps an open question is how many kolams and then
sona there are to the compact, relatively simple 3x2 and 4x2 rectangles.
So for this, you have to look for the possible positions
of the double mirrors with the help of notes on squared paper systematically.
In a second step, you can recognize the sona with the
help of the online program.
Kolam
Game
If you glue the basic figures on
squares of cardboard, you get a game to lay.
...
Miscellaneous
top
Paulus Gerdes
When researching, it becomes clear
that the lusona research was founded and advanced by the scientist Paul
Gerdes. He wrote numerous papers on the subject and gathered many students
around him who studied lusona. He was Dutch, a professor of mathematics
in Mozambique from 1976 and also took up citizenship there.
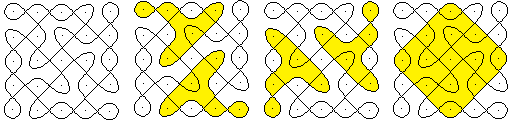
Celtic knots
The 3x3-Kolam and the 4x3-Lusona
become Celtic knots, if you make the lines thicker and place along a line
alternating underpasses and bridges.
Indian
Sand Painting
... ... ... |
Sand image of the North American natives,
fixed with hair setting lotion,
outside the circle four-sided symmetry,
made for tourists,
we bought somewhere near the Grand Canyon, USA. |
German
Beach Painting :-)
... |
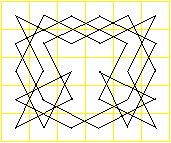
 .......................... .......................... |
Knight's
Tour
... ... ... |
The knight's tour is about the knight moving on the chessboard
in such a way that it (also) describes a closed line.
On the left is a solution for the smaller 6*5 square.
More on my page House of Santa Claus |
References top
(1) South African History Online (www.sahistory.org.za)
(2) https://www.zukunft-irular.de/neue-seite/ (Sona-Geometrie:
Zehn Vögel)
(3) http://www.math.buffalo.edu/mad/special/african-geometry.html
(4) https://www.researchgate.net/publication/256932750_Sona_drawings_mirror_curves_and_pattern_designs
Kolams
und Sona on the Internet top
German
Alban Da Silva (Spektrum)
Mathematik
einer Südseetradition (Sandzeichnungen des südpazifischen
Archipels)
arte.tv
Kolam:
Die flüchtige Kunst der Inderinnen
Henning Krause (Spektrum)
Dr. Henning Krause (Spektrum)
Ethnomathematik
- dargestellt am Beispiel der Sona Geometrie
Labbé
pulli-kolams,
Was
sind Sona?
M. Weber, A. Mischau (Mathematisches
Panorama)
Mathematik
und (bzw. in) andere(n) Kulturtechniken (.pdf-Datei)
Wikipedia
Kolam,
Sona
(Mathematik), Paulus
Gerdes,
Ethnomathematik
, Sandbild,
Sandanimation
English
Darrah Chavey
Mathematical
Experiments with African Sona Designs
Darrah Chavey
Constructing
Symmetric Chokwe Sand Drawings
Forkphorus
Drawing
program
Ljiljana Radovic
MIRROR
CURVES
Marcia Ascher (spektrum.de)
Ethnomathematik:
Die Kolam-Figuren Südindiens
Mattia De’ Michieli Vitturi
Sona
drawings, mirror curves and pattern designs
NN
Sona
- Sand Drawings from Africa
Paulus Gerdes
m-Canonic
mirror curves
Paulus Gerdes
Geometria
Sona de Angola Matemática duma Tradição Africana
Portuguese, 191 pages, lots of illustrations
Slavik Jablan, Ljiljana Radovi,
Radmila Sazdanovi Ana Zekovi
Knots
in Art
South African History Online
Sona
Patterns - Revisiting the Contributions of the People in Sub-Saharan Africa
to Modern Mathematics
Wikipedia
Kolam,
Rangoli,
Lusona,
Sandpainting,
Sand
animation, Sand
mandala,
Ethnomathematics,
Zenigata
Sunae
Youtube
Angolan
Sand Drawings
Some drawings and stories
Youtube
CHIKKU
KOLAM WITH 10-2 DOTS | HOW TO DRAW A SIKKU KOLAM | NELI KOLAM
Example of an Indian floor painting
Youtube
Pongal'
theme for Chennai's Kolam and Rangoli competition
A meeting of women artists
Youtube
Kolam
designs
Collection of videos
Final Remark top
A visitor to my pages, Volker Sayn, pointed out the kolams
and sona to me, which to my own astonishment I had never heard of before.
I have used his extensive documents for this website
and thank him.
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
https://www.mathematische-basteleien.de
©
3/2023 Jürgen Köller
top |






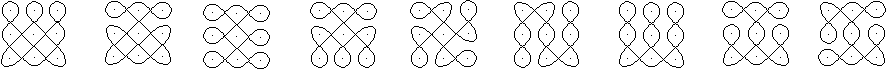






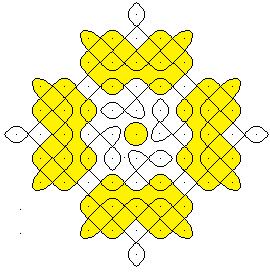
 ...
... ...
...

 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...
 ...
... ...
... ...
... ...
... ...
... ...
... ...
... ...
...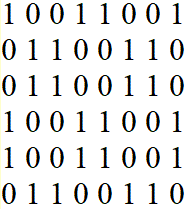 ...
...


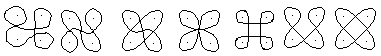


 ...
...
 ..........................
.......................... ...
...