|
Was ist Game of Life?
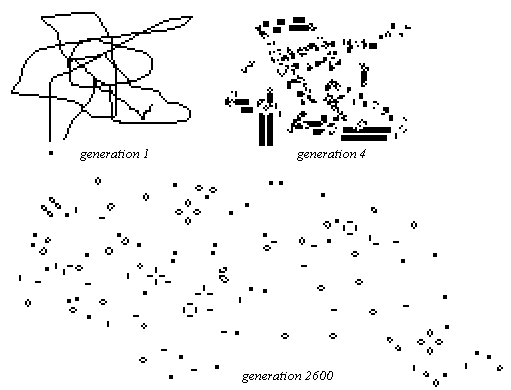
Das Game of Life (Lebensspiel) ist eine Computersimulation.
Lebewesen verteilen sich auf einem unbegrenzten, karierten Feld. Je nach
Nachbarschaft bleiben sie am Leben, sterben oder bringen neues Leben hervor.
Im Beispiel geht man von einer Population von 7 Lebewesen
aus. Sie vermehren sich bis auf 12 und sterben nach 6 Generationen aus
(1, Seite 149ff.).
Game of Life kann auch als zellulärer Automat angesehen
werden, bei dem der Zustand einer Zelle vom eigenen Zustand und von dem
der Nachbarzellen abhängt.
Das Spiel wurde 1970 vom englischen Mathematikprofessor
John Conway entwickelt.
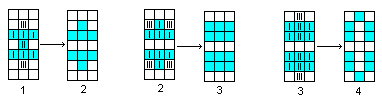
Regeln top
Jede neue Generation wird nach
einer Überlebensregel (I), einer Sterberegel (II) und einer Geburtsregel
(III) ermittelt.
.... .... .... |
Eine Zelle a ist entweder von einem Lebewesen besetzt
oder nicht. Welchen Zustand sie in der nächsten Generation hat, hängt
von der Besetzung der acht Nachbarzellen ab. |
1. Fall: Die Zelle a ist besetzt.
(I) Das Lebewesen in dieser Zelle überlebt, wenn
es 2 oder 3 Nachbarn hat.
(II) Das Lebewesen stirbt, wenn es 0, 1, 4, 5, 6, 7 oder
8 Nachbarn hat.
(Bei keinem oder einem Nachbarn stirbt es aus Einsamkeit,
bei 4 bis 8 wegen Überbevölkerung.)
2.Fall: Die Zelle a ist nicht besetzt.
(III) Gibt es zu dieser Zelle genau 3 Lebewesen in den
Nachbarzellen, so entsteht hier ein neues Lebewesen. In allen anderen Konstellationen
bleibt sie leer.
Anwendung
auf das Beispiel
top
 ... ...
|
Auf diese Weise kann man zu jeder Population schrittweise
die nachfolgende Generation ermitteln. Es genügen Bleistift, kariertes
Papier und Radiergummi. Natürlich ist es besser, die vielen stupiden
Denkschritte einem Computer zu überlassen.
Computereinsatz
top
...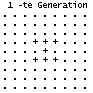 ... ... |
In den siebziger und achtziger Jahren haben sich viele
Computernutzer mit diesem Spiel beschäftigt und ein Programm geschrieben
(links).
Wegen der hohen Auflösung und vor allem wegen der
Schnelligkeit heutiger Computer hat das Lebensspiel eine neue Qualität
erhalten. |
Will man das Spiel des Lebens kennen lernen, sollte man sich
z.B. aus dem Internet ein Programm besorgen und damit experimentieren.
Stillleben top
...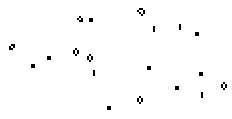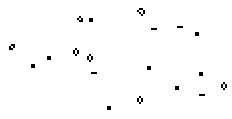 ... ... |
Im Anfangsbeispiel oben verschwand die ausgesetzte Population
nach 6 Generationen.
Bei anderen Ausgangskonstellationen bleiben meist zum
Schluss stabile Populationen (und "Blinker") zurück. |
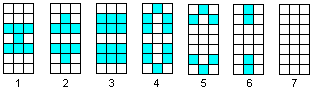
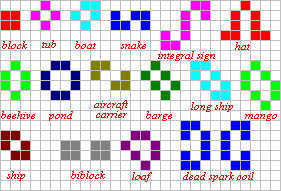
Die stabilen Populationen enthalten
nur Lebewesen mit 2 oder 3 Nachbarn und ändern sich nicht mehr. Sie
heißen nach Conway Stillleben (still lifes).
Hier ist eine Darstellung einiger bekannter Stillleben.
Populationen mit wenigen Lebewesen sind erforscht. Wer sie
gefunden hatte, durfte ihnen einen Namen geben.
Oszillatoren top
... ... ... |
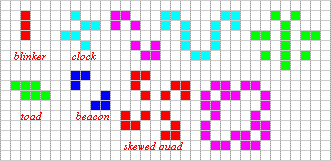
Eine andere auffällige Population ist der Blinker.
Er besteht aus drei Lebewesen, die abwechselnd übereinander oder nebeneinander
liegen. |
Er gehört zu den Periode-2-Oszillatoren (periodic 2
oszillators, p2).
Hier ist eine Zusammenstellung bekannter
p2-Populationen:
Die Perioden können auch größer
als 2 sein:
Links ein Periode-3-Oszillator (p3), das Kreuz (cross), rechts
ein Periode-60-Oszillator in Aktion (p60).
Bewegung top
Gleiter
... ... ... |
Es gibt merkwürdige Gebilde, die sich diagonal auf
dem Feld bewegen. Sie bringen ein interessantes Moment in die Abfolge der
Generationen. Die "Gleiter" bestehen in jeder Phase aus 5 Lebewesen und
haben die "Periode" 4. |
Gleiterquelle top
...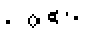 ... ... |
Im Bild links steht eine unscheinbare Anordnung von Lebewesen.
Verfolgt man die nachfolgenden Generationen, so werden gleichmäßig
Gleiter auf die Reise geschickt. |
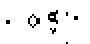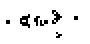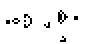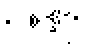 |
Nach jeweils 30 Generationen wiederholen sich die Bilder.
In (amerikanischem) Englisch heißt diese Anordnung
"glider gun".
Eater top
... ... ...
|
Links steht ein "Fresser", der gleichzeitig ein Stillleben
ist. Trifft ein Gleiter an einer bestimmten Stelle und in einer bestimmten
Phase auf ihn, so geht der Eater ungeschoren aus dem Zusammenprall hervor.
Der Gleiter stirbt. |
...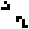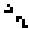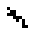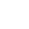 ... ... |
Spaceships top
...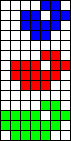 ... ... |
Auch "Raumschiffe" bewegen sich. Es gibt sie in drei
Größen: Sie heißen lightweight spaceship, middleweight
spaceship und heavyweight spaceship, abgekürzt LWWS, MWSS und HWWS.
Die Populationen erinnern sowohl im statischen Zustand
als auch in der Bewegung mehr an Vögel als an Raumschiffe. |
...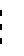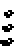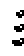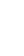 ... ... |
Dreier-Crash top
... ... ...
|
Drei Gleiter bewegen sich aufeinander zu, stoßen
zusammen und dann? |
Populationen
mit einer Geschichte top
Eine beliebte Beschäftigung ist die Entdeckung von
Populationen mit interessanten Verläufen.
Populationen mit wenigen Lebewesen sind erforscht und
katalogisiert.
... ... ... |
Eine bekannte Population dieser Art hat die Form eines
F-Pentominos. Sie hat eine bewegte Entwicklung:
Stillleben und Blinker entstehen, werden wieder aufgesogen
und bilden sich erneut. Insgesamt 6 Gleiter entfernen sich auf Nimmerwiedersehen.
Am Ende bleibt nach 1102 Generationen eine Population mit 15 Stillleben
und 4 Blinkern zurück. |
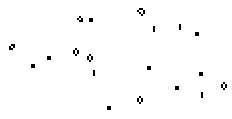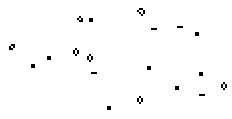 |
Die folgenden Beispiele haben interessante
und zum Teil lange Geschichten. Darauf weisen die Namen hin.
Es ist faszinierend, welche Populationen
aus Hunderten von Lebewesen man sich schon ausgedacht hat. Aus Grundfiguren
werden komplizierte Arrangements zusammengestellt. Es kommt zu vielfältigen
und skurrilen Bewegungsabläufen.
Selbstgemachte
Populationen
top
"Es gibt nichts Gutes, außer
man tut es." Es genügt, auf der Eingabeoberfläche zu kritzeln.
Daraus entwickeln sich unvorhersagbare Populationen.
... ... ... |
Gibt man eine symmetrische Figur vor, so bleibt die Symmetrie
in allen nachfolgenden Generationen erhalten. Dadurch ist sie zu jeder
Phase ansehnlich.
Manchmal hat man Glück:
Wenn man zu Beginn eine Population in Form eines Fensters
13x11 (links) aussetzt, verlassen vier Gleiter die Mitte. Rechts der Moment
der Geburt der vier Gleiter! |
..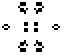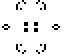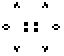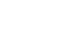 .... .... |
Verwandte Webseiten meiner Homepage
Game of Lifeim
Internet top
Deutsch
beltoforion.de
Das
"Spiel des Lebens"
Steffen Polster (Mathematik alpha)
Game
of Life
Wikipedia
Game
of Life
Englisch
Achim
Flammenkamp
Game of Life
Chris Lipa (Cornell University)
Conway's
Game of Life
Edwin Martin (playgameoflife.com)
John
Conway's Game of Life
Paul Callahan
Patterns
Programs and Links for Conway's Game of Life, What
is the Game of Life? (Wonders of Math)
Stephen Silver's Life Lexicon
Life
Lexicon
Wikipedia
Conway's
Game of Life
Youtube
epic
conway's game of life
Referenzen top
(1) Wilfried Schupp: Schüler programmieren in BASIC,
Paderborn 1980
Kommentar
top
Das Buch von Wilfried Schupp hat
mich damals mit dem Spiel bekannt gemacht. Ich bin nach 20 Jahren wieder
auf "Game of Life" gestoßen. Es ist erstaunlich, welche Entwicklung
diese Spielerei mit einem wissenschaftlichen Ursprung bis zu den heutigen
(geschrieben 2000) schnellen Computern genommen hat. Auch gibt das Internet
jetzt Informationen preis, die mir früher nicht zugänglich waren.
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
https://www.mathematische-basteleien.de/
©
2000 Jürgen Köller
top |
 ...
...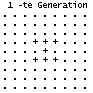 ...
... ...
...

 ...
... ...
...
 ...
... ....
....