What is Tangram?
Tangram is one of the most popular games to lay.
You put figures of 7 pieces together (five triangles, one square and
one parallelogram). You must use all pieces. They must touch but not overlap.
Main Problem top
| All seven tangram pieces consist of half squares with this shape: |
 . |
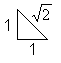There are 32 half squares or 16 squares altogether.
... ... |
You can build a 4x4-square with all the 16 squares. The main problem
of the 'tangram research' is building a square with all the 7 pieces. |
Comments:
You can also choose the smallest tangram piece, the blue triangle,
as the basic triangle. I took the half triangle as the basic form, because
the square built of all seven tangram pieces has the simple length 4.
| Basic triangle on this page: |
............................... |
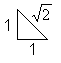Another way: |
 ................ |
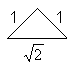The difference is: You have to change the rational und irrational length
of a side.
Building Figures
1st problem: New figures top
... ...
|
You can invent new figures.
A figure is good, if you recognize it by seeing.
There are thousands of figures, which people have already built. |
... ...
|
[3sqrt(2)]x[3sqrt(2)]-squares are possible, if you leave blank one
triangle or two.
|
2nd problem: Filling given shapes top
...... ..... |
You must find the right position of the tangram pieces filling this
shape. (Solution in the end of this chapter) |
3rd problem: How many possibilities are there to
lay the same figure?
top
... ...
|
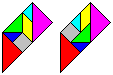You can lay the trapezium in two different ways.
|
Paradoxes
... ...
|
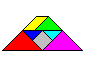This trapezium is not a solution. If you lay this figure, you find
the mistake:
The yellow and the green piece are a little bit bigger.
You use the fact, that 4 and the triple of the square root of 2 (=4.24)
are about the same. |
 |
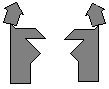Other paradoxes comparing two similar tangram figures, which seem to
be alike.
An example by H.Dudeney
|
Solution:
 |
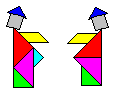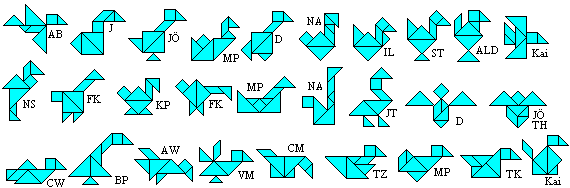
Tangram Birds top
About 100 students (aged 11/12/13) got the task to design birds by
tangram pieces.
Here is a small selection of nice birds.
Not all the students became friends with tangram pieces:
 [= I hate tangrams
;-).]
(Thanks to 6b, 6c, 7a, 7c, 7d in 1999/2000)
Classifying Figures top
You can follow the positions of the sides of the half squares.
1 the sides at the right angle are horizontal
or vertical
2 the side opposite the right angle is
horizontal or vertical
3 mixture of 1 and 2
4 any position
If you have a mathematical point of view, you must allow only 1 and
2.
Nearly all tangram figures belong to model 4. There are many nice and
expressive forms, because there are less rules. They are organized by topics.
Convex Figures top
'A figure is convex', means: If you choose any two points inside the
figure, the whole line between the points must also be inside the figure.
 |
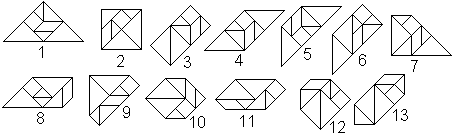Surprising: There are only 13 convex figures, you can build from tangram
pieces. |
Proof by Fu Traing Wang and Chuan-Chih Hsiung in 1942 (Book 4)
Grid Tangrams with
Convex Perimeter top
 |
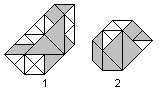You find an interesting suggestion in book 3 and book 4 to classify
tangram figures. This only refers to 'mathematical' figures', which bird
1 and bird 2 (see above) stand for. You can lay them into a coordinate
system, so that the corners of the seven tangram pieces have integers as
coordinates. In other words: You can order the tangram pieces in a way
that the sides with the unit 1 are horizontal or vertical. The lines with
the unit (root of 2) are diagonal. |
The figures are widened by little (white) triangles as necessary, so that
a convex figure develops. These triangles have the same size as the blue
tangram pieces. You count the triangles. Bird 1 needs 14 triangles and
is 14-convex. Bird 2 is 5-convex. The convex figures don't need a triangle.
They are 0-convex. You find all 133 (abstract) 1-convex tangram figures
and solutions in book 4.
There is the problem to find figures with the largest
convex perimeter.
Bruno Curfs proved in (5) that 44-konvex is an upper limit.
Here are Bruno Curfs' seven 41-convex tangrams he found.
...
... ... |
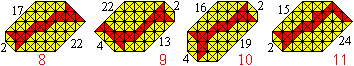I received more 41-convex tangrams:
8 from Ludwig Welther, 9 from Hartmut Blessing,
10 and 11 from Hannes Georg Kuchler. |
... ... |
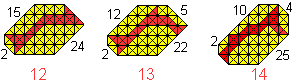Daniel Gronau checked all possible grid tangrams by his computer. He
found out that 41-convex is the upper limit und that there are three more
solutions. |
Making of Tangram Pieces
top
Probably the tangram pieces are developed from cutting a 4x4-square
in pieces.
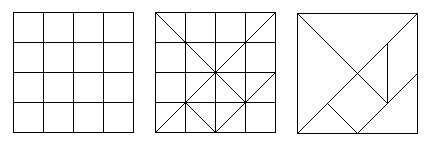You use it to make tangram pieces. You draw a 4x4-square with some diagonals
on plywood or on cardboard. Then you saw or cut the pieces as shown at
the drawing.
Variants of the Tangram
Game top
You can make more tangram games, if you divide simple geometric figures
like square, rectangle or circle. The most famous are (1) "Pythagoras",
(2) "Kreuzbecher", (3) "Alle Neune", (4) "Circular Puzzle",
(5) "The Broken Heart", and (6) "The Magic Egg".
Here is a wide field for designing your own tangram pieces and playing
with them.
Tangram on the Internet top
German
Claus Michael Ringel
Tangram
Grimm's GmbH, Spiel & Holz Design
Legespiele
Herbert Hertramph
Tangram-Spiel
von Jos van Uden, Tangram-Spiel
von Serj Dolgav zum Herunterladen
Landesbildungsserver Baden-Württemberg
Tangram
Sabine Reindl
Tangram
stopkidsmagazin
Tangram
online
tan gram
tangram mit einer galerie von
75 exponaten
Timo Ehmke, Alfred Schreiber
Tangram
online
Urs Tschumi
home
(Tangram-Tisch, Objekte)
Wikipedia
Tangram
English
Andrew D. Orlov
Tangram House
Barbara E. Ford
Tangrams - The Magnificent Seven
Piece Puzzle
Cyberchase (Educational Broadcasting Corporation)
Tangram
Game (Online)
Franco Cocchini
TEN MILLIONS OF TANGRAM
PATTERNS and more
Randy
Tangram
S. T. Han
Tangram Page
Tom Scavo
Tangrams
Wikipedia
Tangram
References (German) top
(1) Pieter van Delft, Jack Botermans: Denkspiele der Welt, München
1998
(2) Karl-Heinz Koch: ...lege Spiele, Köln 1987 (dumont taschenbuch1480)
(3) Rüdiger Thiele, Konrad Haase: Teufelsspiele, Leipzig 1991
(4) Joost Elffers, Michael Schuyt: Tangram, Dumont, Köln 1997
(+ tangram pieces)
(5) Bruno Curfs: Mathematical Tangram, CFF, newsletter of the "Nederlandse
Kubus Club" NKC, 65 (November 2004)
(6) Jerry Slocum, Dieter Gebhardt, Jack Botermans, Monica Ma, Xiaohe
Ma: The Tangram Book, 2003 [ISBN 1-4027-0413-5] Sterling Publishing Company
Feedback: Email address on my main page
This
page is also available in German.
URL of
my Homepage:
http://www.mathematische-basteleien.de/
©
1999 Jürgen Köller
top |
