|
Was ist das Salinon?
...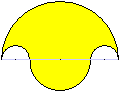 |
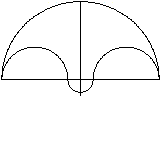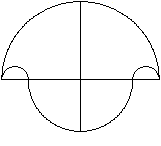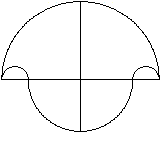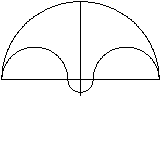
Das Salinon ist eine symmetrische Figur, die aus vier
Halbkreisen gebildet wird.
Ihre Mittelpunkte liegen auf einer Geraden.
Das Wort Salinon kommt aus dem Griechischen und bedeutet
wohl Salzfässchen.
Die Figur geht auf Archimedes zurück. |
Formen des Salinons

Größen
top
Gegebene Stücke
...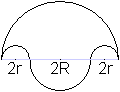 ... ... |
Die Figur wird zum Beispiel durch die Radien des kleinen
und des mittleren Halbkreises festgelegt.
Der große Halbkreis hat dann den Radius R+2r. |
Flächeninhalt
...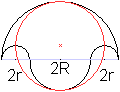 ... ... |
Für den Flächeninhalt gilt A=(1/2)pi(R+2r)²-pi*r²+(1/2)pi*R²=
... =pi(R+r)².
Das Ergebnis kann gedeutet werden als der Flächeninhalt
des roten Kreises mit dem Durchmesser R+(R+2r)=2(R+r). |
Umfang
... ... ... |
Für den Umfang gilt U=Pi(R+2r)+2pi*r+pi*R= ... =2pi(R+2r)
Das Ergebnis kann gedeutet werden als Umfang des roten
Kreises mit dem Radius R+2r. |
Verschiedenes
top
Quadrat im Salinon
...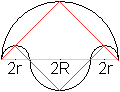 ... ... |
Zeichnet man in die Halbkreise wie angegeben gleichschenklige
Dreiecke, so sind sie nach dem Satz des Thales auch rechtwinklig. Also
liegt schon mal ein Rechteck vor.
Die Katheten dieser Dreiecke sind, der Größe
nach geordnet, a=(1/2)sqrt(2)(2r),
b=(1/2)sqrt(2)(2R) und c=(1/2)sqrt(2)(2R+4r). Die Längen
der Seiten des Rechtecks sind a+b und c=(1/2)sqrt(2)(2R+4r)-a=b+2a-a=a+b.
Damit ist das Rechteck ein Quadrat. |
Inkreis
...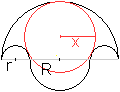 ... ... |
Das Salinon hat einen Inkreis mit
dem Radius x=(R²+3rR+2r²)/(R+3r). |
Zum Beweis
...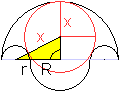 ... ... |
Nach dem Satz des Pythagoras gilt (r+x)²=[(R+2r)-x]²+(r+R)².
Löst man diese Gleichung nach x auf, so ergibt sich
die obige Formel.
Die Rechnung wird dadurch einfacher, dass der Term x²
wegfällt. |
Ausartungen
r=0 führt zum Kreis.

A=pi*R²
U=2pi*R
|
r=R
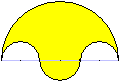
A=4pi*R²
U=6pi*R
|
R=0 führt zu einem Sonderfall
des Arbelos.
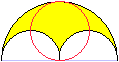
A=pi*r²
U=4pi*r
|
Figuren
aus den vier Halbkreisen
Alle Figuren haben den gleichen Umfang.
Zu dieser Seite passt ein Kapitel
meiner Seite
Halbkreis.
Halbkreisfolge
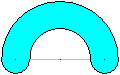
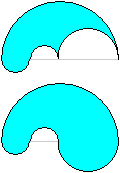
Man kann auf einen Durchmesser kleinere Halbkreise setzen
und deren Anzahl immer mehr erhöhen. Es entsteht eine Restfigur (blau).
Geht die Anzahl der Halbkreise über alle Grenzen, so gelangt man -
theoretisch - zum Halbkreis.
...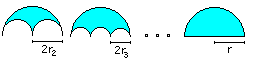 |
Für die n-te Figur erhält man die Fläche
A(n) = (1/2)*Pi*r² - (1/2)*Pi*r²/n. Für n gegen Unendlich
ergibt sich der erwartete Grenzwert von (1/2)*Pi*r². |
Der Umfang der Figur verhält sich merkwürdig.
Er ist für jedes n und auch im Grenzfall gleich
U(n) =2*Pi*r (ungefähr 6,3r).
Der Umfang des Halbkreises andererseits ist wesentlich
kleiner als U(n), nämlich U=(2+Pi)*r (ungefähr 5,1r).
Darin liegt ein Widerspruch zur Anschauung.
Figuren aus Kreisbögen top
...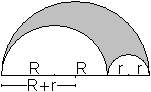 ... ... |
Der hier abgebildete Arbelos
ist auch eine Figur aus Halbkreisen.
Da sie auch auf Archimedes zurückgeht, wird sie oft
in einem Atemzug mit dem Salinon genannt. |
...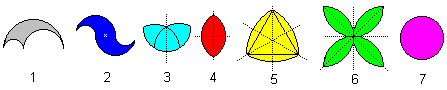 ... ... |
Eine Sammlung von Kreisteilen aller Art findet man hier. |
Frage
... ... ... |
Dank der Wikipedia-Seite http://de.wikipedia.org/wiki/Arbelos
weiß ich, wie der Arbelos, das Schustermesser, aussieht.
Aber wie sieht das Salzfass aus?
Kommt man ihm vielleicht näher, wenn man die Figur
auf den Kopf stellt? |
Salinon im Internet
top
Deutsch
Wolfgang Appell
Der
Salzstreuer
Wikipedia
Salinon
Englisch
Alexander Bogomolny
Salinon:
From Archimedes' Book of Lemmas
Antonio Gutierrez (GoGeometrie)
Geometry Problem 654 : Archimedes'
Book of Lemmas: Proposition 14
Eric W. Weisstein, (MathWorld)
Salinon
Shannon Umberger
Essay
# 4 - The Arbelos and the Salinon
Wikipedia
Salinon
Referenzen
top
Walter Lietzmann: Altes und Neues vom Kreis, Leipzig
und Berlin 1935
Feedback: Emailadresse auf meiner Hauptseite
URL meiner
Homepage:
http://www.mathematische-basteleien.de/
©
2011 Jürgen Köller
top |



 ...
... ...
... ...
... ...
...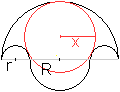 ...
...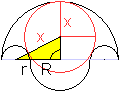 ...
...





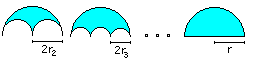
 ...
...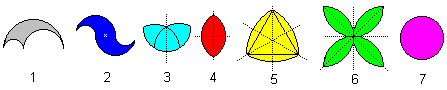 ...
... ...
...